On this page
Why the number of decks matters in blackjack
Introduction
Any respectable source on blackjack will state that there is a positive correlation between the number of decks used in blackjack and the house edge, all other things being equal. In other words, the fewer the decks, the better the odds are for the recreational player. This fact is common knowledge among blackjack players who are at least knowledgeable enough to shop around for a game with good rules. However, I have never seen an in-depth treatment of why this is true. The purpose of this article is to shed light on that question.
Before getting started, let me establish some baseline rules. These were chosen to be as realistic as possible given the blackjack conditions at the time of this writing in 2020:
- Dealer hits soft 17.
- Blackjack pays 3 to 2.
- Dealer peeks for blackjack with a ten or ace up.
- Player may double on any two cards.
- Player may not surrender.
- Player may double after splitting.
- Player may re-split any pair (including aces) up to three times.
- Continuous shuffler used (cards shuffled after every hand).
- Player uses basic strategy.
My blackjack house edge calculator indicates under these rules the house edge is as follows, according to the number of decks:
Blackjack House Edge by Decks
| Decks | House Edge |
|---|---|
| 1 | 0.014% |
| 2 | 0.341% |
| 4 | 0.499% |
| 6 | 0.551% |
| 8 | 0.577% |
These figures may not agree exactly with other respectable sources on blackjack. I believe any differences would be due to either a cut card’s being used or the player’s using optimal composition-dependent strategy. In comparison, I assume the cards are shuffled after every hand and the player always follows total-dependent basic strategy.
Note the difference in house edge is 0.563% between eight decks and one deck. This article shall endeavor to answer the question as to why number of decks has such a significant effect on the odds.
Balanced Game
As a starting point, I consider a simplified blackjack game, in which the rules are exactly the same for both the player and dealer, resulting in a 0% house edge regardless of the number of decks. Then I gradually add actual blackjack rules, one by one, and examine how they affect the house edge by the number of decks.
The initial hypothetical simplified blackjack game shall have the same rules as stated earlier, except:
- Player follows the “mimic the dealer” strategy.
- Winning blackjack pays even money.
- If both player and dealer bust, the result is a push.
The house edge in this Balanced Game is obviously exactly 0.000%, because every rule cuts equally both ways.
Dealer Positional Advantage
Who wins in blackjack when both player and dealer bust? The dealer does. In other words, the dealer enjoys a positional advantage in that the first to bust loses and the player must act first. This is the reason the dealer has the advantage, despite many of the rules that cut the player’s way. Adding this rule to the Balance Game and running it through simulations for one and eight decks results in the following expected returns for the player.
Expected Values by Rule Change
| Rule | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Dealer positional advantage | -8.237% | -8.157% | -0.079 % |
The table above shows the odds are worse for the player in this hypothetical game with one deck compared to eight decks. This is because as the number of decks goes down, the probability of busting goes up. Following is the probability of busting in this “mimic the dealer” game, assuming the dealer plays out his hand even if the player busts first.
- One deck = 27.333%
- Eight decks = 27.209%
The above shows the probability of either side’s busting is 0.124% higher in a one-deck game compared to eight-deck. There is some correlation between each side’s busting, so let’s look at all four combinations of player and dealer busting:
Bust Probabilities
| Player Bust | Dealer Bust | One Deck | Eight Decks | Difference |
|---|---|---|---|---|
| No | No | 44.096% | 44.468% | -0.372% |
| No | Yes | 19.095% | 19.051% | 0.044% |
| Yes | No | 19.095% | 19.051% | 0.044% |
| Yes | Yes | 8.237% | 8.157% | 0.079% |
| Total | 90.524% | 90.728% | -0.204% |
The reason the probabilities don’t sum to 100% is because the table doesn’t count those hands where either side has a blackjack and the hand isn’t otherwise played out. The “Yes Yes” row shows those situations where both sides bust, resulting in a dealer win. It shows this happens 0.080% more often in a single-deck game compared to eight decks. Why? If either side busted, it must have been after hitting a hard hand of 12 to 16 points. This hand must have consisted of at least two cards. Meanwhile, if either side had two high-value cards, it would stand. In other words, hitting generally takes place with hands that have smaller than average-value cards. This removal of small cards in hitting situations causes the remaining cards to have a surplus of high ones. This effect of removal of the small cards before the bust is more significant in a single-deck game.
Blackjack Pays 3 to 2
The next rule we shall add to the Balanced Game will be that a player winning blackjack pays 3 to 2. Adding that rule to my simulation results in the following cumulative player expected returns.
- One deck = -5.912%
- Eight decks = -5.894%
The simulation result table adding a row for the addition of this rule is:
Expected Values by Rule Change
| Rule | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Dealer positional advantage | -8.237% | -8.157% | -0.079% |
| Winning player blackjack pays 3 to 2 | -5.912% | -5.894% | -0.018% |
Taking the difference between the two rows shows the benefit to the player of a winning blackjack paying 3 to 2:
- One deck = 2.325%
- Eight decks = 2.263%
- Difference = 0.062%
This is easy to verify mathematically, as follows. Let d = number of decks. Using Excel notation, the probability of a winning blackjack is: probability(player blackjack) * (1-probability(dealer blackjack)) = (16*d)*(4*d)/combin(52*d,2) * [1-(16*d-1)*(4*d-1)/combin(52*d-2,2)
Probability of Winning Blackjack
| Decks | Probability |
|---|---|
| 1 | 4.649% |
| 2 | 4.578% |
| 4 | 4.544% |
| 6 | 4.532% |
| 8 | 4.527% |
As seen above, the probability of a winning blackjack increases as the number of decks decreases. This is due simply to the effects of removal. For example, assume the first player card is any 10-value card. The probability of this is 4/13, regardless of the number of decks. It is easy to see that in a single-deck game the probability of getting an ace as the second card is 4/51 = 7.843%. In an eight-deck game that probability is 32/415 = 7.711%, which is 0.123% less than in a single-deck game. In simple English, the reason the probability of getting the ace is higher in the single-deck game is the deck is richer in aces after you remove a 10 from it. The same is true if the first card is an ace; the remaining cards will be richer in tens in the single-deck game.
Furthermore, if the player does get a blackjack, the probability of the dealer’s getting one goes down as the number of decks goes down. This is because the player’s removing an ace and a 10 from the deck in a single-deck game makes it much more difficult for the dealer to get a blackjack compared to an eight-deck game. To be specific, the probability of a dealer blackjack, assuming the player has one already, is 3.673% with one deck and 4.605% with eight decks. The player wins an extra half unit with every winning blackjack. To get the value of a winning blackjack’s paying 3-2 to our hypothetical balanced game, take the probability of a winning blackjack and multiply by 0.5 for that extra half unit each time. This results in a player advantage by number of decks as follows:
Player Edge from Winning Blackjack
| Decks | Player Edge |
|---|---|
| 1 | 2.325% |
| 2 | 2.289% |
| 4 | 2.272% |
| 6 | 2.266% |
| 8 | 2.263% |
Note that the mathematically calculated benefits of a winning player blackjack’s paying an extra half unit match the simulation results shown earlier for single- and eight-deck.
The table below shows a running list of the rules analyzed to this point and their benefit to a single-deck player compared to eight decks:
Effect of Rules
| Rule | Single-Deck Benefit |
|---|---|
| Dealer positional advantage | -0.079% |
| Winning player blackjack pays 3 to 2 | 0.062% |
| Total | -0.018% |
Next, let’s analyze the benefit to the player of being allowed to stand on a hard total of 12 to 16. The total-dependent basic strategy in this range is the same for any number of decks, as follows:
- With a total of 12, stand against a dealer 4 to 6, otherwise hit.
- With a total of 13 to 16, stand against a dealer 2 to 6, otherwise hit.
Adding this strategy to the simulation results in the following player expected returns:
- One deck = -2.209%
- Eight decks = -2.625%
The simulation result table below includes a row for the addition of this rule:
Expected Values by Rule Change
| Rule | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Dealer positional advantage | -8.237% | -8.157% | -0.079% |
| Winning player blackjack pays 3 to 2 | -5.912% | -5.894% | -0.018% |
Taking the difference between the second row and the third shows the effect of the player’s having free will to stand on a hard 12 to 16.
- One deck = 3.703%
- Eight decks = 3.270%
- Difference = 0.433%
Taking the difference of these two figures shows the effect of this rule change is worth 0.433% more to the player in a single-deck game compared to eight decks. Contrary to popular belief, this explains the majority of why a single-deck game is worth 0.563% more to the player than an eight-deck game.
Looking more deeply at what happens when the player stands on stiff totals of 12 to 16, while the dealer cannot ‒ this table shows the benefit to the player from various events that change due to the player’s hitting fewer stiff totals, resulting in fewer player busts, and more dealer busts, as well as the dealer’s losing more face-offs:
Possible Outcomes when Player Stands on Hard 12 to 16
| Event | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Fewer player-only busts | 6.282% | 6.271% | 0.010% |
| More dealer-only busts | 4.228% | 4.171% | 0.057% |
| Fewer both bust | 4.228% | 4.172% | 0.055% |
| Player wins fewer face-offs | -1.914% | -2.039% | 0.125% |
| Dealer wins more face-offs | -9.121% | -9.306% | 0.185% |
| Total | 3.703% | 3.270% | 0.433% |
The same table has been simplified to show the benefit of winning more due to the dealer’s busting more often and losing more face-offs:
Summarized Possible Outcomes when Player Stands on Hard 12 to 16
| Event | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Player busting less benefit | 14.738% | 14.615% | 0.123% |
| Face-off loss | -11.035% | -11.345% | 0.310% |
| Total | 3.703% | 3.270% | 0.433% |
To put it in plain English, in a single-deck game the player will bust 14.738% less frequently than the dealer by following basic strategy with a hard total of 12 to 16. However, of those hands, 75% of the time the dealer will not bust, resulting in the dealer’s winning in a face-off with a player hand of 16 or less that can’t win. Relative to all hands, the player saves 14.738% by busting less but gives back 11.035% in the form of more face-off losses, for a net gain of 3.703% in a single-deck game.
This benefit is only 3.270% in an eight-deck game. All things considered, the benefit of strategic standing on 12 to 16 is worth 0.433% more to the player in a single-deck game than in eight decks.
Why is strategic standing more valuable in one deck vs. eight decks? The answer is similar to that of why the dealer’s positional advantage is more significant in a single-deck game. There is more busting going on in the single-deck game. Although busting more can cut both ways, it cuts against the player more because he loses when both sides break. Those totals of 12 to 16 when the player stands are likely composed of more small cards than large. This leaves more high cards left in the deck to potentially bust the player. The effects of removal of these low cards the player needs to improve his hand are more costly in a single-deck game than in eight decks. In other words, hitting stiffs is more dangerous in the single-deck game. Standing instead is more beneficial in a single-deck game.
Here is an updated table of the cost/benefit of each rule change:
Effect of Rules
| Rule | Single-Deck Benefit |
|---|---|
| Dealer positional advantage | -0.079% |
| Winning player blackjack pays 3 to 2 | 0.061% |
| Player may stand on hard 12 to 16 | 0.433% |
| Total | 0.415% |
Player May Double
Next, let’s analyze the benefit to the player of being allowed to double. To study the effect, I had the simulation follow the appropriate doubling strategy for the given number of decks, which appears later in the article. Adding this strategy to the simulation results in the following player expected returns:
- One deck = -0.556%
- Eight decks = -1.245%
This simulation result table includes a row for the addition of this rule:
Expected Values by Rule Change
| Rule | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Dealer positional advantage | -8.237% | -8.157% | -0.079% |
| Winning player blackjack pays 3 to 2 | -5.912% | -5.894% | -0.018% |
| Player may stand on hard 12 to 16 | -2.209% | -2.625% | 0.415% |
| Player may double | -0.556% | -1.245% | 0.689% |
The difference between the third row and the fourth shows the effect of the player’s having free will to double, as follows:
- One deck = 1.653%
- Eight decks = 1.380%
- Difference = 0.273%
Taking the difference of these two figures shows the effect of this rule change is worth 0.273% more to the player in a single-deck game compared to eight decks. This explains another significant portion of why a single-deck game is worth 0.563% more to the player than an eight-deck game.
Why is doubling more valuable in a single-deck game? Most of the time when the player doubles it will be on a hard total of 9 to 11 points. Doubling is done with two cards, so it must take two smaller-than-average cards to add to a low total of 9 to 11. If two small cards are removed from a single deck of cards, the next card has a 32.00% chance of being a ten, which is obviously good when doubling on hard totals. Meanwhile, if two small cards are removed from an eight-deck shoe, the effect of removal is not as strong, decreasing the probability that the next card is a ten to 30.92%.
Here is an updated table of the cost/benefit of each rule change. Note that the total benefit of 0.689% exceeds the final house edge difference. This is because we have not yet considered the effect of splitting.
Effect of Rules
| Rule | Single-Deck Benefit |
|---|---|
| Dealer positional advantage | -0.079% |
| Winning player blackjack pays 3 to 2 | 0.061% |
| Player may stand on hard 12 to 16 | 0.433% |
| Player may double | 0.273% |
| Total | 0.689% |
Player May Split
Next, I analyzed the benefit to the player of being allowed to split. To study the effect, I had the simulation follow the appropriate splitting strategy for the given number of decks, which appears later in the article. Adding this strategy brings us to the full basic strategy. There are no other rule differences between player and dealer to study after adding splitting. The full basic strategy player expected returns are:
- One deck = -0.012%
- Eight decks = -0.575%
The simulation result table including a row for the addition of this rule is:
Expected Values by Rule Change
| Rule | One Deck | Eight Decks | Difference |
|---|---|---|---|
| Dealer positional advantage | -8.237% | -8.157% | -0.079% |
| Winning player blackjack pays 3 to 2 | -5.912% | -5.894% | -0.018% |
| Player may stand on hard 12 to 16 | -2.209% | -2.625% | 0.415% |
| Player may double | -0.556% | -1.245% | 0.689% |
| Player may split | -0.012% | -0.575% | 0.563% |
The difference of the fourth row and the fifth shows the effect of the player’s having free will to split.
- One deck = 0.544%
- Eight decks = 0.669%
- Difference = -0.125%
Taking the difference of these two figures shows the effect of this rule change is worth 0.125% less to the player in a single-deck game compared to eight decks.
The reason splitting is more beneficial in an eight-deck game, compared to one, is that the chances of getting a pair in the first two cards is more. To be specific, with eight decks, to use Excel terminology, the probability is 13*combin(4*8,2)/combin(52*8,2) = 7.470%. With one deck the probability is 13*combin(4*1,2)/combin(52*1,2) = 5.882%.
Recall also that the base game rules allow for re-splitting up to three times or to four hands. If two cards of the same rank are removed from a single deck, the probability of getting that rank on the next card is 2/50 = 4.000%. Meanwhile, for an eight-deck shoe, this probability is 30/414 = 7.246%. With less splitting and re-splitting happening in a single-deck game, the value of splitting overall is less. This explains why the benefit of splitting decreases going from eight to one deck.
To add the negative effect of splitting to the single-deck game completes our table of the effect of various rules on the benefit of a single-deck game compared to eight decks.
Rule Single Deck Benefit Dealer positional advantage -0.079% Winning player blackjack pays 3 to 2 0.061% Player may stand on hard 12 to 16 0.433% Player may double 0.273% Player may split -0.125% Total 0.563%Note that the sum in the lower right cell of 0.563% matches the differences given by the house edge calculator quoted at the beginning of the article. Here is the same table listed in order of effect:
Effect of Rules
| Rule | Single-Deck Benefit |
|---|---|
| Dealer positional advantage | -0.079% |
| Winning player blackjack pays 3 to 2 | 0.061% |
| Player may stand on hard 12 to 16 | 0.433% |
| Player may double | 0.273% |
| Player may split | -0.125% |
| Total | 0.563% |
Basic Strategy Tables
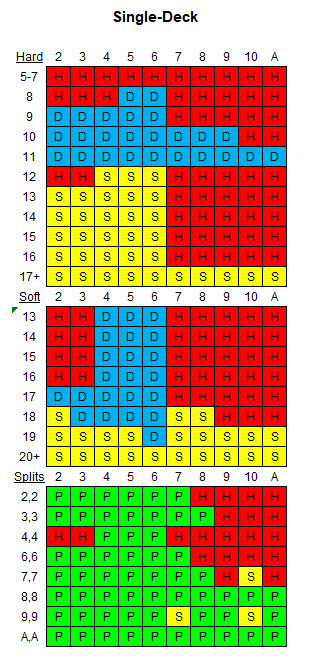
The following table shows the appropriate basic strategy for the given rules and one deck.
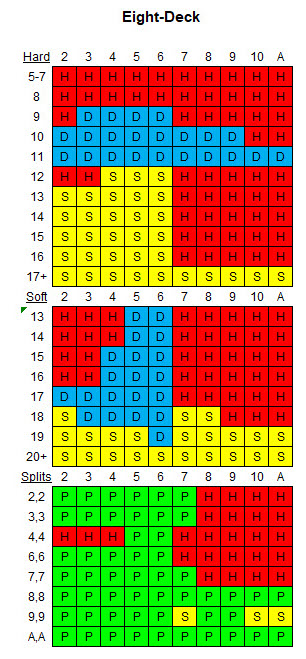
The following table shows the appropriate basic strategy for the given rules and eight decks.
Expected Value Tables
The following table shows the expected value of each initial hand in the single-deck game. The top row shows the dealer’s up card. Expected values are measured before the dealer checks for blackjack. The total column shows a weighted average of the expected values in each row according to the probability of receiving the hand. The lower right cell shows the expected value of the overall game.
Expected Values in Single-Deck Game
Expected Values by Player Hand vs. Dealer Up Card with One Deck
| Player | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0.0227 | 0.0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0.0104 | 0.0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0.0528 | 0.0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0.0199 | 0.0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0.0151 |
| 10 | 0.4262 | 0.4908 | 0.5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0.5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0.0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 13 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0.3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0.0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0.4364 | 0.6101 | 0.5769 | 0.2642 | 0.0125 | -0.1586 | 0.2644 |
| A,2 | 0.0402 | 0.0711 | 0.1174 | 0.2130 | 0.2455 | 0.1074 | 0.0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| A,3 | 0.0184 | 0.0447 | 0.1127 | 0.2042 | 0.2391 | 0.0605 | 0.0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| A,4 | -0.0103 | 0.0237 | 0.0892 | 0.1753 | 0.2191 | 0.0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| A,5 | -0.0298 | -0.0019 | 0.0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| A,6 | 0.0142 | 0.0743 | 0.1549 | 0.2805 | 0.2630 | 0.0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| A,7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0.0459 |
| A,8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| A,9 | 0.6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0.0943 | 0.5871 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| A,A | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0.4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0.0396 | 0.1235 | 0.3014 | 0.3378 | 0.0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0.0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5,5 | 0.4441 | 0.5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0.1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0.0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0.0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0.2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0.0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| Total | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0.0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
Expected Values in Eight-Deck Game
Expected Values by Player Hand vs. Dealer Up Card with Eight Decks
| Player | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0.018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0.0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0.0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0.0076 | 0.0427 | 0.0774 | 0.1079 | 0.0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0.0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0.0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0.5253 | 0.5723 | 0.3990 | 0.2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0.5264 | 0.5759 | 0.6271 | 0.6718 | 0.4653 | 0.3496 | 0.2271 | 0.0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 13 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0.4372 | 0.4513 | 0.6153 | 0.5918 | 0.2848 | -0.0149 | -0.1753 | 0.2569 |
| A,2 | 0.0458 | 0.0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0.0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| A,3 | 0.0224 | 0.0507 | 0.0827 | 0.1366 | 0.2010 | 0.0769 | 0.0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| A,4 | -0.0006 | 0.0294 | 0.0641 | 0.1328 | 0.1986 | 0.0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| A,5 | -0.0211 | 0.0088 | 0.0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| A,6 | -0.0006 | 0.0558 | 0.1220 | 0.1933 | 0.2513 | 0.0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| A,7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0.0270 |
| A,8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0.5953 | 0.2878 | -0.0164 | -0.1795 | 0.2579 |
| A,9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0.5752 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| A,A | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0.0697 | 0.1700 | 0.2643 | 0.0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0.0500 | 0.1502 | 0.2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0.0080 | 0.0441 | 0.1066 | 0.2027 | 0.0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5,5 | 0.3676 | 0.4201 | 0.4748 | 0.5324 | 0.5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0.0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0.0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0.1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0.0585 |
| 10,10 | 0.6334 | 0.6442 | 0.6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0.5745 |
| Total | 0.0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0.0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
Differences in Expected Value (in %)
The following table shows the expected value in the single-deck game less the eight-deck game on a percentage basis.
Change in Expected Values by Player Hand vs. Dealer Up Card (x100)
| Player | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ace | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0.05 | 0.664 | 0.361 | 0.087 | -1.52 | 0.22 |
| 6 | -0.8770 | 0.0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 13 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0.0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0.0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0.1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| A,2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| A,3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| A,4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| A,5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| A,6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| A,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| A,8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0.0390 | 1.5550 | -1.4310 | 1.0640 |
| A,9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| A,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| A,A | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0.0090 | -1.4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| Total | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
Further Reading
‘The Theory of Blackjack’ by Peter Griffin gives the best treatment of the topic of this article that I have seen. He addresses the subject in chapter 8, titled: “Many Decks and Different Rules,” which uses a different baseline set of rules and calculates the difference between one deck and infinite decks. He doesn’t always give exact numbers for everything, but paraphrases the breakdown of the 0.69% difference under his assumptions as follows:
- Doubling Down: Almost half of 0.69%
- Player blackjacks: 0.07%
- Splitting: More than offsets the benefit of blackjacks
- Standing on 12 to 16: “Presumably the remaining discrepancy.”
Griffin goes on to list the benefit of various rule changes under both one deck and infinite decks.
Acknowledgments
I would like to thank Don Schlesinger for his wise counsel on the analysis and proofreading of this article.


