Blackjack - FAQ
How does the house have the advantage in Blackjack?
The dealer has the advantage because the player has to go first. If both of you bust it isn't a tie, but YOU lose.
What would be the best way for one to win a blackjack tournament. I seem to do quite well in regular play, but can never come out in the top two to advance. It seems third place is the best I can do.
One could write an entire book on blackjack tournament strategy. Briefly, here are some pieces of advice:
- Positional advantage is very important. When you are last to act is the best time to take chances with big bets.
- Bide your time at the beginning. Sometimes on a cold table everyone else will burn themselves out while you coast to first place at your table.
- The second half of the round take big chances to get in first place.
- If competing against one other player you want to bet with him when ahead, and contrary to him when behind.
- Pay attention to the maximum bet allowed. If the maximum bet is small compared to the player stacks you should get aggressive early.
First let me say I love your site and will be visiting each of the advertisers to help support it. I hope you are doing very well financially as you are undoubtedly saving a lot of people a lot of money. It is amazing what I see in the casinos and will recommend your site to anyone who will listen (most losers won’t, I get a lot of heat when I hit a 12 vs a dealer 2 even when I explain the math). My question is do you have any advice for Blackjack players participating in Blackjack tournaments? I have participated in a few and have came very close to advancing to the "money" round with no real strategy other than stay close to the leaders on the table and bet it all on the last hand. Any advice would be greatly appreciated!
Thanks for the kind words. I appreciate the thought of visiting the advertisers. However the casinos don’t care about click throughs as much as they used to and now what matters is new real money players, and how profitable those players are. So unless you might actually play there is no pressure any longer to click through the banners.
Blackjack tournaments are not my strong subject. For advice on that I would highly recommend Casino Tournament Strategy by Stanford Wong. Wong says that if you are behind to bet opposite of the leader, small when he bets big, and big when he bets small. If you are in the lead then you should bet with the second highest player. The book gets into much more detail. Speaking of supporting my site, it helps to click through my Amazon links when buying books there.
First of all, I can’t commend you enough for your web site and information that you continue to detail not only online, but on TV and in your newsletters. I know I can always turn to you whenever I have a thorny question about gambling math.
My question relates to what has come to be known in certain blackjack circles as The Flaw. In a nutshell it says that the original creators of basic strategy programmed a flaw into their calculations which has been recreated over and over again by other mathematicians when they’ve come up with their basic strategy. As one proponent of ’The Flaw’ proclaims, "only 3 others that know post on this board. One is the recently retired IBM type, who confirms that to find the Flaw a computer simulation would have to be programmed to do so-therefore prior knowledge is REQUIRED. The math boyz are certain that they are right; but Thorp can’t figure why so few win. One percent says it all."
So, what is The Flaw, and is there any truth to it? Or is it theoretically BS? I know it’s easy to dismiss the nay sayers out of hand, but I’m intrigued.
Thanks for the kind words. This "flaw" theory is a load of crap, which is not surprising considering the cesspools where talk of it is usually found. It isn’t the case that one person created the basic strategy and every other blackjack expert just copied it. Numerous mathematicians have developed the basic strategy from scratch and have all come up with the same thing. I find it highly unlikely that every one of them, including me, programs in the exact same flaw.
It’s my understanding Casino’s put a lot of emphasis on a Player’s theoretical win. I would imagine my theoretical value has a direct correlation to compatibility from a house point of view. If I am a $10.00 average Player in Blackjack and play an average of 3 hours per trip, what is the formula a casino uses to determine my theoretical value? Thank you in advance.
Yes, the casinos do calculate the value of a player’s play and then comp back a certain percentage, roughly about 33% to 40%. According to my theoretical house edge table, the casinos assume a house edge of 0.75% in blackjack. So in your example the value of this play would be 0.0075×$10×60×3=$13.50. If the casino comps back 1/3 of the play then you could expect to get a comp worth $4.50. However, most places don’t like to fuss with such small comps.
Where are the single deck games in Vegas that still pay 3 to 2?
With the demise of Binion’s Horseshoe the number of true single deck games in Vegas has fallen by about 75%. Although it isn’t a priority of mine to keep up to date on this some that I know of are the Fiesta Rancho, Golden Gate, El Cortez, and the Western. Beware of single deck games that only pay even money or 6 to 5 on a blackjack, you are much better off at a shoe game that does pay 3 to 2.
I was at the Luxor this week and I noticed a blackjack machine that looked much like a video poker machine. Do these things use random generators like online, or do they work like slot machines?
Using a random number generator _is_ the same as working like a slot machine. Online blackjack, slot machines, and video blackjack all use random number generators.
It is a Nevada state law that an electronic game with representations of cards or dice must be based on fair odds. So the game should be fair with odds the same as in a hand dealt game having the same rules.
I’ve read quotes similar to this on a couple of different sites: "If the dealer won 40 hands in a shoe and you won 20, this trend is likely to continue until you are broke or until the unfavorable bias is removed through many shuffles". That seems like somewhat "extreme" wording to me but my question is, is there any validity to that concept? Might any clumps of generally favorable (high), or unfavorable, cards make it through one dealer shuffling such that a non-shuffle tracker might take advantage by varying his bets to capitalize on short streaks? By the way, your site kicks ass.
Thanks for the compliment. This theory is called card clumping and would make for good fertilizer if it could be bagged. No legitimate blackjack writer puts any stock in it at all.
What are the pros and cons of burning a card on a blackjack shoe game, when a new dealer taps onto the table?
Unless you are counting cards it doesn’t make any difference. If you are counting cards then it is like decreasing the penetration by one card.
I have some questions on tipping etiquette...
Blackjack: Can I double, split or take insurance for the dealer?
Caribbean Stud Poker: Can I (or do I have to) raise also for the dealer?
Let It Ride Poker: Can I place more than one bet for the dealer (what happens if I decide to take back one of my bets and there was a tip)?
Craps: Can I play a tip everywhere I can play (odds and props included)?
Roulette: Can I play on numbers for him?
As a general rule, you can make any bet for the dealer in any game. In general you should tell the dealer which bets are his, except blackjack where its common practice that any bet outside the betting circle is for the dealer.
Blackjack: Yes to all three. The usual way to bet for the dealer in blackjack is to put the tip on the edge of the betting circle. If you split or double most people also split or double the dealer’s bet, although it is not required.
Caribbean Stud Poker: I asked a dealer and he said raising for the dealer is optional. I haven't studied it but I think this would result in the tip having an advantage.
Let it Ride: I'm told that the player should put out three tips initially but must pull them back in the same manner that they pull back their own bets. Bets that are pulled back go to the player, not the dealer.
Craps: Yes, you can make any bet for the dealer. The most common ones are the yo-11 and the hard ways. If you make a line bet for the dealers and back it up with the odds it is implied the odds are a tip too.
Roulette: As in craps you can make any bet for the dealer. Just tell them in advance.
We recently went to Casino Niagra in Canada I was playing blackjack with a full table of players. The play went around the table as normal, I stayed on 17. When it came to the dealer she had an 8 showing flip her unshown card was a ten equals 18. She then proceeded to take a hit on 18 (by mistake)and threw up a Jack which was a bust on 18. I felt this should have been a misdeal or a push for all but the dealer said no it was not valid since the house rules are dealer Stays on 17 and above and Hit on 16 and all below. I disagreed with the call and the pit boss came over and stated the dealer is correct and you lose. I sure would appreciate your thoughts as I totally disagreed with the call. Plus I had a large bet riding so maybe it is just my sore losing side coming out. I sure can’t wait to get an experts thought on this once and for all.
I side with the casino. The rules state the dealer stands on 18. The dealer has no free will and once she got 18 the 18 is firm. The extra card dealt does not alter the dealer’s 18 and it was correctly burned. In a one or two deck game some casinos will reshuffle in that situation.
Why is it better odds for the casino to hit on a soft 17? It seems they would be more likely to bust and hence have worse odds.
It is true the casino busts more often if the dealer hits a soft 17. However the dealer also gets fewer seventeens, which is not a very good hand. It is to the dealer’s advantage to hit a soft 17 for the same reason the player should always hit or double on a soft 17. A 17 is a lousy hand, and whether the player or the dealer hitting a soft 17 offers two chances to improve upon it.
We have all been at blackjack tables where it appears the dealer cannot seem to lose. Assuming you cannot count cards and the dealer is winning 3, 4 or 5 hands in a row, is there any assumptions one can make about the count or is all just random? Do you get up and leave (and/or reduce your bet) and go to another table on the theory that the count is against you and that is why you are losing. Or, do you just assume that the past has no influence on the next hand and continue on. What would the Wizard do? I know hunches have nothing to do with it but, particularly in Blackjack, are there any mathematical conclusions one can draw about the future from the fact that the dealer has been winning (or losing for that matter) for what seems like an inordinate amount of time.
Actually, if the dealer has been winning it is slightly likely that it is because lots of small cards have come out, which would mean the deck is rich in large cards, in which case the odds would actually bend in your favor the next hand. But this is a very slight effect and nothing you should be trusting in. I think in these situations you have just been having bad luck and switching tables will not help. Lest some perfectionist correct me I will say that between shuffles blackjack hands do have a slightly negative correlation. If you had asked about roulette or craps I would say the past makes no difference at all. It would also say that about blackjack if a continuous shuffler were used. However I can’t absolutely say blackjack hands are independent for the reason I just explained.
I have a Blackjack question that I did not see already answered on your site. How would the house edge change if the player always got a glimpse of the dealer’s hole card and changed his strategy accordingly?
According to my calculations this would give the player about an 8.8% advantage under optimal strategy. The optimal strategy is the same as that of double exposure in most cases. However if you think the dealer will expose his hole card again I would recommend not making it obvious that you know and not make plays that normally look ridiculous (like hitting a 19 against a 20) .
I’ve seen video blackjack in several LV casinos and am wondering if the game is regulated in a similar fashion as video poker. If so, would playing the games using basic table blackjack strategy give the player the best payback percentage? If not, is there a basic strategy for video blackjack?
Yes. Any video representation of a card game in the state of Nevada must be dealt from a fairly shuffled deck. In other words you should expect the same kind of outcome as in a live game with the same rules. So basic strategy tables will also work for video blackjack.
[Bluejay adds: Every video blackjack game I’ve seen pays only even money on naturals, which significantly increases the house edge.]
A friend of mine told me that the casinos also have video blackjack. Are the odds or randomness the same for both methods? I mean do the video programmers give the casinos a better house edge with the video version of blackjack vs. the table version, or is the video version programmed exactly to mirror the table game?
It is a law in Nevada that video representations of card games must be truly random. Thus the odds would be same as in live blackjack with the same rules. Most other jurisdictions more or less accept Nevada regulations. You should be warned that the vast majority of video blackjack games pay even money on a blackjack, which is a terrible rule whether on a video or live game.
Your strategy cards for Blackjack I presume is basic strategy for the initial cards (player's first two cards and dealer's up card). However, after hitting or splitting the deck composition has changed and the basic strategy may have changed. What I think would be more appropriate is a basic strategy based on the overall game of blackjack, including after splitting and hitting. Is there any situation where your initial hand basic strategy and one for the overall game are different?
Yes, my basic strategy charts are designed to be the best play based on the first two cards. This is the usual approach to developing the basic strategy. One benefit to this approach is the expected values of each play can be calculated exactly and compared to other sources. However, you bring up a valid point. So I asked Don Schlesinger, author of Blackjack Attack, if there were any known play where the best play on the initial hand is different from the best play to maximize the expected value of the overall game of blackjack. He replied that a soft 18 against a dealer ace, in a double-deck game, where the dealer stands on soft 17, was such a play. As my blackjack appendix 9 shows the expected value for standing is -0.100502 and for hitting is -0.100359. So, based on the first two cards, the odds favor hitting by 0.000143. However, there are many more ways to see soft 18 than one ace and one seven. The following table shows all the ways this hand can turn up.
Soft 18 Vs Ace Combinatorial Analysis
| Player cards |
Conditional Probability |
Hit EV |
Stand EV |
Hit Return |
Stand Return |
| A7 | 0.621139169 | -0.100359 | -0.100502 | -0.062336906 | -0.062425729 |
| A6A | 0.036728229 | -0.11202 | -0.116009 | -0.004114296 | -0.004260805 |
| A52 | 0.146912917 | -0.111299 | -0.103382 | -0.016351261 | -0.015188151 |
| A43 | 0.146912917 | -0.114804 | -0.103721 | -0.01686619 | -0.015237955 |
| A5AA | 0.001827682 | -0.111395 | -0.105122 | -0.000203595 | -0.00019213 |
| A42A | 0.016814677 | -0.116975 | -0.108233 | -0.001966897 | -0.001819903 |
| A33A | 0.007356421 | -0.132142 | -0.107256 | -0.000972092 | -0.00078902 |
| A322 | 0.020470041 | -0.134229 | -0.11004 | -0.002747673 | -0.002252523 |
| A4AAA | 0.000073486 | -0.117554 | -0.110984 | -0.000008639 | -0.000008156 |
| A32AA | 0.001028802 | -0.134775 | -0.112433 | -0.000138657 | -0.000115671 |
| A222A | 0.000709873 | -0.136788 | -0.114993 | -0.000097102 | -0.00008163 |
| A3AAAA | 0.000002238 | -0.135313 | -0.114821 | -0.000000303 | -0.000000257 |
| A22AAA | 0.000023502 | -0.137312 | -0.117376 | -0.000003227 | -0.000002759 |
| A2AAAAA | 0.000000046 | -0.137859 | -0.119823 | -0.000000006 | -0.000000006 |
| Total | 1 | -0.105806844 | -0.102374694 |
Explanation of column titles
Player cards:Cards in player’s hand
Conditional probability: Given that the player has a soft 18 against a dealer ace the probability of the given hand composition.
Hit EV:Expected value by hitting
Stand EV:Expected value by standing
Hit Return:Product of probability and hit expected value
Stand Return:Product of probability and stand expected value
The right two cells of the bottom row show that overall the expected value of hitting is -0.105807 and for standing is -0.102375. So, the table shows the odds favor standing by 0.00343.
To confirm these results I ran two simulations under the rules in question, one simulation hitting and one standing on this play. I counted only hands where soft 18 against a dealer ace happened at any time during play. Here are my results.
Soft 18 Vs Ace Simulation
| Soft 17 | Hands Played |
Total Win |
Expected Value |
| Stand | 3857490 | -396224 | -0.102715 |
| Hit | 3208390 | -337572 | -0.105215 |
So, the simulation shows the odds favor standing by 0.0025 over all possible scenarios where this hand turns up. Thus, for practical purposes of playing all hands, the best play is to stand, contrary to what my basic strategy chart says.
I have a question about a blackjack tournament, where only the largest stack at the end is paid. Assume 1000 players start with 100$ in chips and can bet 5 hands at a time, from 1-10$ per hand. If no one knows anything about the other chipstacks, what chipstack should you be looking for before being satisfied?
You didn’t say how many rounds there were. However, I would bet $10 in all five hands every hand, or go bust trying. With 1,000 players and a relatively low max bet you’ll need all the variance you can get.
In your recent Ask the Wizard column (169) someone asked a question regarding the dealer incorrectly burning a card in a blackjack game. At the casino I work at, when dealing blackjack if a card is incorrectly removed from the shoe and is NOT exposed it is still the next card in play (unless it is dealt to the dealers hand, in which case it is burnt). In Blackjack a card is only burnt a) When starting a new shoe, b) When a card is boxed (facing the wrong way in the shoe), or c) Incorrectly dealt to a dealers hand.
Thanks for your comments. That sounds more or less like the usual policy in Vegas as well.
Playing blackjack, at what average dollar bet can I Expect:
- Free Food & Beverage
- Free Lodging
- One of those high roller suites
- Free golf at Wynn
- A new car
- Free airfare.
The basic formula for comps is that the casino will give you back a percentage of your theoretical loss. That percentage can vary by game, the higher the house edge the higher the percentage. I asked a former Vegas casino manager and he said the comp rebate is about 15%. Other pertinent pieces of the equation are 60 hands per hour in blackjack with an average house edge of 1%. So the value of comps you could expect would be (average bet) × (hours played) × 60 × 1% × 15%. Let’s assume 16 hours of play. You can then back out the average bet required. Let’s assume food and beverage has a value of $500. Then the average bet required would be 500/(16*60*0.01*0.15) = $347. A free room might be worth $1,000, so an average bet of $694 would be required. There is a whole spectrum of suites, roughly ranging in value from $1,000 to $10,000 a day, so an average bet of $1,389 to $13,889 would be required. Free golf might be worth $500, so back to $347 for that. I’ve heard of Vegas casinos comping shopping sprees at the Fashion Show mall, but they don’t sell cars there. If we assume $2,000 for airfare then $1,389. At high levels of play this may also be subject to skill level, the better you are the less you will get. They also might have some sympathy and give you more than you are entitled if you had a really bad run of luck. For rooms, you will have more bargaining power if you ask for one during a slow time when they have vacancies anyway.
I am a part time blackjack player with a lot of success in land based casinos. I am thinking to start playing online but I have a few questions about this. Does a payout percentage of for example 98% mean that you lose 2% anyway regarding good or bad play. In European blackjack with no hole card, if you play last box isn't it better to leave the little card for the bank or must I hit anyway? sometimes i have my doubs about this. P.S. love your site THANKS
Thanks. Payout percentages such as this are historical. For example King Neptune's casino posts their June 2006 report on their web site. The 96.78% for table games means that in June 2006 the ratio of money returned to money bet was 96.78%. In other words an actual house edge of 3.22%. Your own results will depend on the game rules, your skill (in games of decision making), and luck. In most games the odds are quantifiable so payout reports are not useful. It shouldn't matter to you how badly other players have played or the mix of games they chose. Where these reports are very useful is in evaluating the slots. No casino that I know of volunteers how loose their slots are theoretically set, but such payout reports gives the user a good idea. If looking at other months you see that King Neptune's pays about 96% in slots. I also think it is a good sign of a good operation to have return percentages independently verified. It shows the casino has nothing to hide.
In regards to your Wizard Ace Five Count, what effects does real casino play versus your simulation have on the bank role needed to have a reasonable risk of ruin. More specifically, is your simulation played head to head with a dealer, where when the count is high you are betting the higher bets more times per shoe than at a real table where 6 players are using up cards when the count is high, resulting in fewer chances to bet when the count is high. Thank you.
Measured in terms of the house edge, the number of other players doesn’t matter. Yes, they will eat up cards when the count is good, but they will also do so when the count is bad. In the long run it doesn’t matter. However, in terms of expected wins per hour, when you have an advantage, it helps to have fewer players, because you will play more hands in the same amount of time.
I am going to Las Vegas next weekend and like to play $5 blackjack & Let It Ride on the tables. Will I be able to find an open $5 table on a weekend or should I plan on bringing more funds than usual with me? If $5 tables are few and far between, where might I find them?
It will be difficult finding $5 blackjack on the Strip on a weekend. You’ll probably have to settle for a low-roller casino like the Riviera, Sahara, Frontier, or Circus Circus. It will be a lot easier downtown. Let It Ride is slowly fading away, but if you find it the minimum unit is usually $5.
Playing blackjack on a continuous shuffling 5-deck system, are the odds of winning different than playing the dealer with 1 deck or 2 decks?
For the beneit of other readers, my blackjack appendix 10 explains, the house edge in a five-deck game is 0.028% less if a continuous shuffler is used, as opposed to a hand shuffle. The difference between five decks and two decks, all other rules being equal, is 0.18%. So the two-deck game without a shuffler would be much better. Let’s compare a 5-deck continuous shuffler game to a 4-deck hand shuffled game. As my blackjack calculator show difference in house edge between four decks and five decks is 0.0329%. So the benefit of a continuous shuffler is worth less than removing a single deck.
I am a regular blackjack player at a 50-table casino. There are some dealers I have identified that, when I am playing 6th or 7th position, expose their facedown card perhaps 25% of the time. I am wondering what the proper play would be without them being moved right away. I am afraid to take full advantage of seeing the card. If I know the dealer has 20 should I still hit with a 19 or would that draw too much heat? Or should I wait on it and take advantage in more marginal situations?
That is what my blackjack appendix 16 is for. To answer your question, I wouldn’t make any plays that would set off a red flag, like hitting a hard 19. My advice is stick to more marginal, believable, errors.
As part of my desire to increase my game knowledge, as a casino dealer, I began reading your site years ago. I seem to remember reading that the dealer’s average non-blackjack winning hand is 18.56. Today, as an instructor, I sought that fact to show my students and was unable to locate it. What is the correct answer and how is it calculated? Thank you.
The table below shows the average dealer score, assuming the dealer does not bust, and the dealer already checked for blackjack, according to various rules. Note how the average score increases with the number of decks. More importantly, note that the average score is 0.0405 higher when the dealer hits soft 17. The probability that the dealer will bust is only 0.00403 higher when the dealer hits a soft 17. That is 10.05 extra dealer points per dealer bust. This, hopefully, goes to show why it is bad for the player if the dealer hits a soft 17.
Average Dealer Total in Blackjack
| Decks | Stand Soft 17 | Hit Soft 17 |
| 1 | 18.840371 | 18.880098 |
| 2 | 18.842648 | 18.882868 |
| 3 | 18.843415 | 18.883798 |
| 4 | 18.843826 | 18.884288 |
| 5 | 18.844053 | 18.884564 |
| 6 | 18.844205 | 18.884720 |
| 7 | 18.844292 | 18.884880 |
| 8 | 18.844370 | 18.884981 |
To answer your second question, I used a brute force combinatorial program in C++ to cycle through all the possible combinations of dealer hands.
When I am in Vegas I like to play a friendly game of $5.00 blackjack. To my surprise, on this trip, the $5.00 blackjack table had either disappeared or they were paying 6 to 5 on a blackjack. I played a fair $5.00 game at the El Cortez but was hard pressed to find another casino that provided a $5.00 table with reasonable rules. Do you know of other fair $5.00 games either on the Strip or downtown? Thank you. I wish I had discovered your web site before my recent trip.
Many casinos are indeed paying 6 to 5 on blackjack in their low-limit games, and it is getting worse quickly. However, there are still real blackjack games out there at a $5 minimum. The other rules likely will not be the best, in particular six decks with dealer hitting on soft 17, but at $5 you can’t be too picky. It sounds like you were in town on a very busy weekend, or just didn’t look very hard. Any downtown or off-Strip casino should have some real $5 blackjack tables. Those tables are usually the most crowded. On Strip you should be able to find some token $5 games, especially mid-week, at properties such as the Excalibur, Monte Carlo, Harrah’s, Flamingo, Circus Circus, Riviera, and the Sahara.
I love the site; thanks for all the hard work. The blackjack survey is great and I notice that most casinos have more than one set of rules. Can I rightly assume that the better the rule set, the higher the table minimum at a given casino? For example, the lowest house edge at the Bellagio is quite good but does the table have $100 minimums?
Thank you, and you’re welcome. Yes, it is generally the case that the better the rules, the higher the minimum bet.
Every time I go to the Blackjack games there is a grumpy simple individual, who wants to stone some poor soul for "messing up the shoe.” Is there any truth to this?
In ten years of running this site I steadfastly denied the myth that bad players cause other players to lose in blackjack. However, you are the lucky 1000th person to ask, so I took the trouble to prove it by random simulation. The rules I put in are the standard liberal Vegas Strip rules as follows.
6 decks
Dealer stands on soft 17
Double on any first two cards allowed
Double after split allowed
Late surrender allowed
Player may re-split to four hands, including aces
Cut card used
First, I had both players follow correct total-dependent basic strategy. Over almost 1.6 billion rounds, the loss of the first player to act was 0.289%, and the second player to act of 0.288%.
Second, I had the first player follow the same correct strategy, and the second player follow the same correct strategy except:
Always hit 12 to 16
Always double 9 to 11
Split any pair
Never surrender
Never soft double
In a simulation of 1.05 billion hands the loss of the first player was 0.282%, and the second player was 11.260%. So the house edge of the basic strategy playing first player was almost the same, regardless of whether the second player played correctly or wildly incorrectly. I hope this puts and end the third baseman myth, but I doubt it. As I have said many times, the more ridiculous a belief is, the more tenaciously it tends to be held.
This is an etiquette question regarding the blackjack tables, which I haven’t been able to find on your site. I go to my local casino about once a month with my friends, we just play for fun pretty much, but they don’t know the game that well, nor have basic strategy learned or memorized. My question is: when we’re all playing at the table together, is it wrong for me to give them advice on how to play their hand? Tell them to split, double down, stand etc., will this annoy the dealer or other players? Is it right or wrong to do this?
Thanks for an awesome site! I get lost in your odds calculations sometimes, but it’s just so damn informative!
Thank you for the kind words. It would be perfectly acceptable to give advice in that situation. In general, it is acceptable to give solicited advice, even to strangers. The dealers don’t like it when a player gives unsolicited advice. It gets into a grey area if it isn’t clear whom a player is soliciting advice from. If the player seems to be asking the dealer, then you shouldn’t advise. When in doubt, my policy is to keep my mouth shut.
What does the effect of not burning a card have on a single-deck blackjack game, if any.
If you aren’t counting cards, then it doesn’t matter. If you are, then any burned cards should be added to the number of cards left unplayed in the deck/shoe, when making the true count conversion.
I have always heard a rumor that casinos invented basic strategy. Where did the basic strategy come from?
John Patrick is probably behind that rumor. The basic strategy was first published in the September 1956 issue of the Journal of the American Statistical Association. The article was titled “The Optimum Strategy in Blackjack” by Roger R. Baldwin, Wilbert E. Cantey, Herbert Maisel, and James P. McDermott. Collectively, they are known today as the “Four Horseman of Aberdeen,” because they worked at the Amberdeen Proving Ground in Maryland at the time they did the analysis. I’m proud to have a copy of that article, and to have seen three of the four Horseman, when they were inducted into the 2007 Blackjack Hall of Fame. It has since been derived from scratch by hundreds of people, including me. If done properly, under the same rules, the results always agree. Then again, maybe I’m just in on the conspiracy.
Why do casinos burn cards in blackjack and baccarat?
A minor reason is to foil card counters. However, instead of burning x cards, the dealer could move the cut card x cards forward, and achieve the same purpose. The major reason is game protection. For one, the player might catch a glimpse of the top card, and alter his bet and strategy, based on this information. Such a tactic would not be cheating, I might add. The top card is also vulnerable to lots of cheating schemes. It could be marked, the dealer could peek at it, or force a desired card to the top. If for any reason the dealer knew what the top card was, he could signal that information to a confederate player, giving him a huge advantage.
This issue has bothered me for many years. In 1999, my father took me to Vegas for my 21st birthday. We were playing blackjack at the same table, I with roughly $25 in bets on the table, my father with about $40. The dealer had 20, but miscalculated and thought she busted. She paid us as if we won. Roughly 15 minutes later, three suits came down, put their hand on our shoulders, essentially appraised us of the situation, and mandated that we pay back the "winnings" or leave the casino. We decided to leave the casino, and gamble elsewhere that evening. Is that standard operating procedure or is this more the exception to the rule?
In my opinion the two most sacrosanct things in gambling are no cheating, and honoring a bet. No expiration dates, no excuses, a gentleman honors his gambling debts. You didn’t say how many points you had. The right thing to do would be to return the winnings only if you had a 20, or the winnings plus the original wager if you had less than 20. If they were rude in the way they asked, I wouldn’t blame you for leaving, but I still would have paid. I’ve been asked this before, so I think that this is the standard operating procedure.
In Las Vegas can I use a hint/cheat sheet chart while sitting at a Blackjack table?
Yes, as long as it doesn’t slow down the game too much for other players.
Do you have any information on video blackjack? Do the rules/payoffs vary, and where are the best games in Vegas?
I think your odds are best with the big Table Master units with big video screens housing attractive dealers. These are getting easier and easier to find, but I don’t know of any specific list of them. Your odds of finding them will be better in low-roller casinos. Some pay 3 to 2 on blackjack, and some only pay 6 to 5. An an example, the unit at the Riviera has the following rules:
- 6 decks (shuffled after four decks)
- Blackjack pays 3 to 2
- Dealer hits soft 17
- Double after split allowed
- Double on any two cards allowed
- Surrender allowed
- Split to two hands only
- Seven Card Charlie (un-busted hands of 7 cards automatically win)
- Bet range: $2-$200
The house edge under these rules is 0.68%. If you play an even-money game, the house edge will be 1.4% to 2.0%, depending on the other rules. Be sure to use a player card to earn whatever cash, free play, or comps the casino offers.
The picture below shows one of these products.

What is the effect of player mistakes in blackjack?
Peter Griffin devoted a whole chapter to that question in his book Extra Stuff — Gambling Ramblings. His study was based on observing 11,000 actual hands of play in 1987. The following table summarizes his results of the cost of errors made.
Cost of Blackjack Errors
| Location | Cost of Errors | Margin of Error |
| Atlantic City | 1.13% | 0.12% |
| Las Vegas | 1.67% | 0.17% |
| Reno | 1.48% | 0.19% |
| Lake Tahoe | 1.39% | 0.54% |
| Total | 1.41% | 0.10% |
In my opinion, play has improved a lot in the 23 years since the study. If forced to guess, I think the cost due to errors is about 0.5% now. I would agree with Griffin that Atlantic City players are more skilled than Vegas players.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
After this column first appeared, I heard from gaming consultant Bill Zender. He offered to let me post his article How Poor are Blackjack Players (PDF 147K), from Gaming Operations magazine. There is says his own research showed the cost of player mistakes to be about 0.83%.
There is a blackjack game online with the following rules:
- 8 decks.
- Cards shuffled after every hand.
- Blackjack pays 2 to 1.
- Dealer hits on soft 17.
- No doubling down.
- Split pairs once only.
- No surrender.
Using my blackjack house edge calculator, I get a house edge of 0.82%, before factoring the 2-1 on blackjacks and no doubling. 2-1 on blackjacks is worth 2.26% to the player. No doubling is worth 1.37% to the dealer.
So I show the player edge is 0.82% -2.26% + 1.37% = 0.07%.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Do you have any comment on the guy who recently won $15 million in Atlantic City?
To me, the key clue is this sentence from the article, "'They also agreed to discount 20 percent of his blackjack losses as an incentive to get him to play,' he said." With liberal blackjack rules, a well-financed player can easily have a strong advantage with a 20% rebate.
The proper strategy is to quit when you have either achieved a huge win or a moderate loss, whichever comes first. For example, winning $1,000,000 or losing $100,000. Most of the time you will lose, so it takes a big bankroll to weather the ups and downs. Fortunately for the player, he was properly financed to take advantage of such offers. Besides having an advantage, he may also have exceeded expectations since December. I salute him for his success.
Now that the Barona has removed their single-deck blackjack game, what is now the best blackjack game in America for the basic strategy player?
You are correct. In June the Barona sadly removed their single-deck game, which allowed doubling on any two cards, double after splitting, and surrender. The basic strategy house edge was 0.01%. According to the Current Blackjack Newsletter, that was the best game in America.
So, who rises to fill the top position? According to my own Las Vegas rule survey, the best game is now at the Hacienda casino, near Hoover Dam. However, I don't keep track of anything outside of the greater Vegas area, so I checked the Current Blackjack Newsletter, which monitors the entire U.S. and Canada. They indicate the Hacienda game is not only best in Vegas but the best anywhere in the U.S. and Canada. So, I congratulate the Hacienda for rising to the number one spot!
The rules of said game are:
- Single deck
- Blackjack pays 3-2 (of course)
- Dealer hits soft 17
- Double any first two cards
- Double after split
- Re-splitting aces allowed
- No surrender
- Table limits: $2-$200
- Game not always open
Based on my blackjack house edge calculator, the house edge is 0.02%, assuming basic strategy and no cut card. To get this figure, take the "realistic house edge" and subtract 0.11%, what the cut-card effect otherwise costs the player in a single-deck game. Al Rogers, with the Current Blackjack Newsletter, tells me that both the Hacienda and the Peppermill casinos, mentioned below, do not use a cut card, in favor of dealing a specified number of rounds per deck. Single-deck games usually follow the rule of six, which means the number of rounds per deck is equal to max(2,6-p), where p is the number of players.
For players who want to bet over $200 in single-deck games, Al suggested I put in an honorable mention for the Peppermill group of casinos (Peppermill, Montego Bay, and Rainbow) in Wendover, Nevada. They have the same rules, except no double after a split, for a house edge of 0.16%, again assuming basic strategy and no cut card. That is probably the best single-deck game that is open 24-hours and doesn't mind large bets.
Shameless Plug: The Current Blackjack Newsletter lists the rules and card-counting conditions for every legitimate casino with table games in the U.S. and Canada. The monthly reports are $15 each, $30 per quarter, or $99 per year. I've been using it as an invaluable resource for over a decade.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I've tried to turn my friends on to your Wizard's Simple Blackjack Strategy. However, they find it still too difficult, especially the soft 18 exception. Can you offer anything even more simplified?
Okay, how about this "Extra Simple Strategy." Follow the first rule that applies.
- Split eights and aces.
- Double 10 and 11.
- Hit hard 9 or less.
- Hit hard 12 to 16 against a 7 to ace.
- Hit soft 17 or less.
- Otherwise, stand.
That is just 30 words, counting the numbers as words. The cost due in errors relative to the full basic strategy is 0.44%. That is a lot more than the 0.14% of my full Simple Strategy, but is still about half the cost of errors made by the average blackjack player.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Hi, I live in Iran. I read your site and enjoyed your comments about blackjack, in which i have a great interest. I like to play and use your chart in the game, but it's difficult for me to visit Las Vegas, where great casinos exist with very little house edge. Since I live in Asia, I would like to know where I can find fair casinos to play blackjack with a fair house edge, besides Macau.
It isn't every day I get a gambling question from Iran. I could be wrong, but based on a look at the World Casino Directory, the closest casino I can find that has confirmed blackjack is the Zodiac Casino in Amaty, Kazakhstan. Their web site indicates that they have roulette, blackjack, and 6 Card Poker (whatever that is). Unfortunately, I can't vouch that they are fair or have competitive rules.
What is the effect of removing a single particular card (2 to ace) from a six-deck shoe in blackjack?
The following table shows the effect on the player's expected return by removing one card from a six-deck shoe, according to whether the dealer hits or stands on a soft 17. For example, if the dealer stands on soft 17, and the burn card is a five, then the house edge drops by 0.146%.
Effect of Removal in Blackjack
| Card | Stand Soft 17 |
Hit Soft 17 |
|---|---|---|
| 2 | 0.069% | 0.071% |
| 2 | 0.070% | 0.072% |
| 3 | 0.084% | 0.089% |
| 4 | 0.114% | 0.122% |
| 5 | 0.146% | 0.148% |
| 6 | 0.079% | 0.085% |
| 7 | 0.041% | 0.038% |
| 8 | -0.010% | -0.012% |
| 9 | -0.041% | -0.046% |
| 10 | -0.092% | -0.098% |
| Ace | -0.101% | -0.091% |
The table above assumes otherwise "liberal Strip rules," which allow double after split, late surrender, and re-splitting pairs (including aces) up to three times. The table was created using the Composition Dependent Combinatorial Analyzer at bjstrat.net.
Normally in 6-5 blackjack the player can't take even money. What would be the effect to the house edge if he could?
Assuming six decks, allowing even money in 6-5 blackjack, which the player should take if a blackjack pays only 6-5, then it lowers the house edge by 0.06%.
I know that I am not supposed to play 6-5 blackjack, but should I find myself in this situation is there any time that it would be advantageous to double down on a blackjack instead of taking the 6-5 payout?
Using the Hi-Lo count, I show that against a dealer 5 and blackjacks pay 6 to 5, and if the true count is +18 or greater, then you should double on a blackjack. Not that you asked, but if a blackjack paid 3 to 2, then you would need to get to a count of +27 to double. These numbers should be considered as estimates. Against any other dealer up card, the count would need to be even greater for doubling to be the right play.
This question was raised and discussed in my forum at Wizard of Vegas.
I think casinos that shuffle the cards early in a good count are cheating. I'm going to file a formal complaint with the Gaming Control Board against the Stratosphere for doing this to me. No particular question, I just wanted to vent.
Shuffling early, as a defense against card counters, has been part of game for 50 years. I would say that if casinos were using computers to tell the dealer when the count was good, as a hint to shuffle, that would be cheating. I also think if the dealer counted himself and shuffled early on recreational players, that too would be cheating. However, if the dealer is doing it when you raise your bets, well, that is just the way the game is played. If you won your case with Gaming, the casinos would ruin the game for counters, like they did in Atlantic City over the Ken Uston lawsuit. The next thing you would see is every game on a continuous shuffler. Both sides would be better off to leave the cat and mouse game as it is.
This question is raised and discussed in my forum at Wizard of Vegas.
Do bad players, in particular in blackjack, cause everybody else to lose?
No. While everyone remembers the time a bad player took the dealer's bust card and caused the whole table to lose, people tend to forget the times that a bad player saved the table. This practice of selective memory to support pre-existing beliefs is called “confirmation bias.” In the long run, bad players are just as likely to help you as hurt you, so leave them alone.
Why do you say not to take "even money" on a blackjack when the dealer has an ace up? It is a sure winner!
There is a 69.1% chance the dealer doesn't have a blackjack and you'll win the full 3-2. (1.5 × 69.1% = 103.7%.) That’s more than the 100% you get by taking even money. You’ve already established the fact that you're a gambler by playing in the first place. Don't suddenly become risk-averse and give up that 3.7% because you don't want to take a chance.
In blackjack, sometimes the dealer unknowingly exposes the hole card. What is the player advantage when this happens?
The player advantage is 10% +/- 0.5%, depending on the specific rules. Here is the strategy when the dealer exposes both cards. This is different than the double exposure strategy, where the player loses on ties.
Your task is to get from square 0 to square 19. You may not take a path of the same color twice in a row. In other words, at every square you must change to a path of another color. No u-turns. What is the solution?
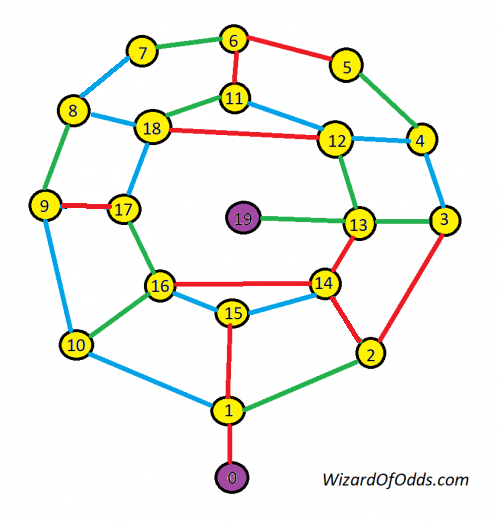
Puzzle by David Pleacher.
I encourage my readers to solve this for themselves. However, if you give up, you may click the solution button below.
Here is one possible solution: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 17, 18, 12, 11, 18, 17, 9, 8, 7, 6, 5, 4, 3, 2, 1, 15, 14, 13, 19.
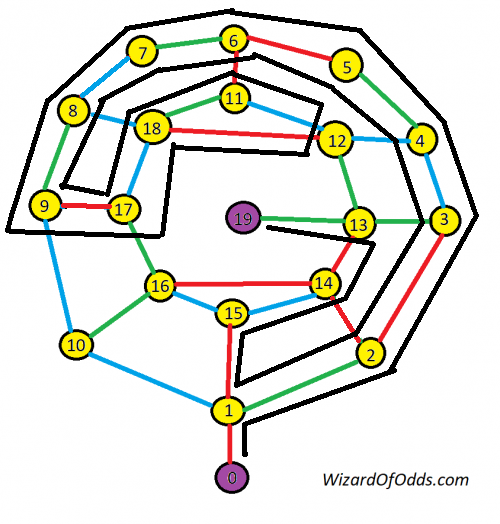
The key is to notice that you can make a u-turn in the 11-12-18 triangle. The solution is to go the whole way around the outside circle, in a counter-clockwise rotation until you get back to 1. Then take the inner circle clockwise to 18. Then make a u-turn and get back to 18. Then retrace your steps back to 1. Then it is an easy path to 19 from there.



