Roulette - FAQ
How would you fare if you played roulette like this -- bet $5 on both 0 and 00, bet $15 on two of the columns. Wouldn't you have like a 70% of winning?
You would have a 2/38 chance of winning $140, a 24/38 of winning $5, and a 12/38 chance of losing $40. The overall expected return is [(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5.26%. The same house edge as on every bet in double-zero roulette (except the 0-00-1-2-3 combination, which is 7.89%).
Suppose I were to stroll into a casino and place a bet on 2 of the 2-1 payoffs in roulette, such as $100 on 1-12 and $100 on 13-24. In a one time deal, aren't my odds of taking home $100 a generous 63%? I'm not talking about the long run; just a one-time bet.
You're right the chances of winning are 24/38, or about 63%. However you have to risk $200 to only win $100. If you want to increase your chances of winning even more then bet on any 35 numbers. The probability of winning will be 92%.
Is there a way of combining bets in roulette to maximize one's odds? For example, a dozen bet pays out 2 to 1. If I place two dozen bets, say the first and second set of 12, I have a 63.16% chance of having it pay off. These are better odds then a simple red/black, even/odd, or high/low bet. Although I really only gain 1 to 1 rather than 2 to 1(if I win, since part of my bet has to lose since the winning number cannot be in both the first and second set of twelves), the odds have been slightly shifted in my favor by combining two bets. Have the odds on these sorts of combinations been determined? If they have been, where might I be able to find them?
As long as you stay away from the 0-00-1-2-3 combination, the house edge on any combination of bets is always exactly 1/19, or 5.26%. There are ways to increase your probability of winning, but at the cost of winning less relative to your total wager.
I was playing roulette last nigh using the "Martingale" method of doubling down twice after the 1st loss. Dumb, I know, but I usually don't lose much and I gamble a long time. Anyway, what ended the game for me was I was betting even, and in four rolls the number 9 came up in three of the spins. What are the odds of that? Does that sound suspicious? For that matter, have casinos ever been caught cheating?
The probability of getting any number three times out of 4 is 38*4*(1/38)3*(37/38) = 1/5932. However, if you play long enough you almost can't help but notice unusual events like this. This does not nearly rise to the level of being suspicious. Cheating does occur in real casinos. It is usually a rogue dealer who is caught by casino security. There have been some strong cases of cheating made against online casinos but no governmental authority has ever convicted anyone to the best of my knowledge.
Isn't it an even worse roulette betting strategy to bet multiple numbers on the inside during one bet (as most players do) vs. making a sequence of independent bets on one number? For example, if one had $100, betting 10 bets of $10 dollars on the number "8" would lose less than betting $10 on 10 numbers on one spin? It seems to me that "hedging" just guarantees that certain (in the above case 9 bets) will ALWAYS lose? You don't address "hedging" on your page?
See my Ten Commandments of Gambling. The sixth commandment is "never hedge thy bets." About your roulette question, the probability of losing all ten bets by betting one at a time is (37/38)10=76.59%. The probability of losing all ten bets by betting them all at once on different numbers is (28/38)=73.68%. By hedging, or betting ten numbers at once, you lower your probability of a total loss but also limit your maximum win to $26. The player betting one at a time could win up to $350. Both these methods have the same total expected return of 94.74%.
I read your page on systems and I have been telling people this for years! I deal roulette in a casino and I have seen all of the systems at one time or another. I have seen one system that, even though on a computer simulation might not work (probably won’t), "Seems" to work in real life. That means that I have seen it win more than lose.
The way it works is a player will put $75 dollars on the 1 to 18 $50 dollars on the 3rd 12 and $10 dollars on the 0-00 split for a total of $135 dollars. This covers all but six numbers (19 through 22) and will yield a 15 dollar payout every time the ball misses those 6 numbers EXCEPT when 0 or 00 hits in which case it's 40 dollars. I know it sounds nuts!!! But trust me, I'm here to tell you I have seen it win more than lose. It also works in reverse (duh). I would love to know the true odds of this system, but it's hard to tell someone that it doesn't work when they are walking off my table 2 grand richer:-)
There are 30 ways to win $15, 6 ways to lose $135, and 2 way to win $45 (not $40). The expected return of this combination of bets is ((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -.0526, or 5.26%, the house edge on any one bet or combination of bets as long as the dreaded 0-00-1-2-3 combination is avoided. In your observations you have likely seen fewer than expected 19-24 occurrences, which accounts for the illusion that this method is winning.
Say, Wizard I was wondering about roulette. With the boss media software, you can spin the wheel without actually placing a bet. Isn't this in the player's favor? With some of the roulette betting systems I have seen, like the Martingale you double up when you lose and such. Can't you just watch the wheel without placing a bet and based on the previous spins place your bet. An example would be to spin the wheel 5 times before placing a bet. Suppose that all the numbers were odd. Wouldn't it make sense to begin playing the wheel by betting on even? I know this kinda buys in to the gambler's fallacy and the wheel doesn't care what the last spin was, but also the probability diminishes with each spin that an odd number will continue to come up. Am I on to something or just going over an old theory?
You're just rehashing the gambler's fallacy. If the ball landed in odd 100 times in a row on a fair wheel the odds that the next spin would be even are still the same as every spin, 47.37% on a double zero wheel. So it does not help that you can spin without betting. The ball does not have a memory.
While Roulette clearly cannot be beaten by chance, I have heard that it can be beaten by physics two ways (in theory). Way one: a high tech device, which measures the velocity of the ball against the velocity of the wheel and predicts the outcome sector of the wheel with like a 40% accuracy. Way two: Wheel bias. Obviously a wheel would have to have a bias of at least 5.26% to get the player to an even keel. The question is, how many spins would you say, Wizard, does it take to determine wheel bias, if there is any?
I've heard of both these techniques being used. I don't know much about devices to clock wheels, except they are known to exist and be used from time to time. Here in Nevada such a device would be highly illegal. Taking advantage of biased wheels I hear a lot more about. It has been done lots of times. I think casinos with old wheels are the most vulnerable target. I've been saying for years that I think Argentina is a ripe target for that.
When playing the Martingale double-up system against the single-zero roulette wheel on any one of the even chances. I figured that you will lose one time in every 248 sessions. Meaning a session that runs to completion with either a win of one unit or a loss of 255 units. Am I figuring correctly, if not could you please give the correct odds?
If the maximum loss is 255 units then you can bet up to 8 times. The probability of losing eight bets in a row is (19/37)8=.004835. So, you have 99.52% of winning one unit, and 0.48% of losing 255 units.
On average, in single-zero roulette, how often will a number repeat (ex. two 8s in a row) over the course of 36 spins?
You can expect a repeat once every 37 pairs of numbers. So, with 36 numbers we have 35 pairs of numbers. So, the expected number of repeats is 35/37 = 0.9459.
Everybody says that roulette cannot be beaten in the long run with mathematical systems. But, how can you explain the fact that there are professional gamblers who make their living at roulette? I don't think it's just boasting. They actually win more than they lose with everyday playing.
Show me someone who is winning at a fair game of roulette and I'll show you somebody who is just lucky, and will likely lose it all back. You can only skillfully beat roulette by advantage play, like exploiting a biased wheel, or clocking the wheel.
I have read everything you have to say about roulette, but see nothing about roulette spinners. Under the watchful eye of the pit boss the roulette spinner throws "sections" to improve the odds of the house. The spinner that can throw greens, not every time but with good percentages of time, maybe one out of 7 or 8 when he wants to wipe out a large progressive better.
Casinos don’t need to resort to such tactics to win. Furthermore casinos have nothing to fear from progressive bettors. Most of the time progressive bettors win, but the few that hit their bankroll limits pay for all the winners and then some more for the casino. Furthermore it would take a great deal of skill to deliberately spin a ball into a specific section. I don’t believe it can be done with any marked degree of accuracy.
Hi Wizard, you’ve got a great site. In double 0 roulette, I realize all the bets have the same high house edge, but I’m just finishing a stats course and it seems to me that not all the bets are quite the same due to their standard deviations. A $1 bet on Red, for instance, has an S.D. of 1.012019 while a $1 bet on a single number has an S.D. of 5.839971, according to my calculations. Thus, the expected probability of coming out ahead over 1, 100, and 10000 trials, respectively is 0.4793, 0.3015, and 0.0000 for an even-money bet, and 0.4964, 0.4641, and 0.1837 for a single number bet. Is my analysis correct? (I assumed normality) Thanks!
Thanks for the compliment. First of all the standard deviation on any even money bet is 0.998614 and on a single number is 5.762617. The probability of coming out ahead by flat betting even money bets over 1, 100, and 10000 spins is 0.473684, 0.265023, and 0.00000007 respectively. The probability of coming out ahead by flat betting single number bets over 1, 100, and 10000 spins is 0.0263158, 0.491567, and 0.18053280 respectively. It seems you are trying to argue that single number bets are better because of the higher probability of finishing ahead over multiple bets. This is true, however the probability of a substantial loss is also much greater. Over a session the expected results always fall somewhere on a bell curve. With low volatility bets like red or black that bell curve is sharp and doesn’t stray far from a small loss. With high volatility bets like single numbers the bell curve is wide, allowing for a much wider range of net results, both good and bad.
My co-worker D. insists that he has perfected a way to consistently win at Roulette. I’m not convinced. Is he just lucky or is there any system that works?
He is just lucky. As I have said thousands of times, no betting system can pass the test of time.
I read your topic in Roulette on the Martingale method. I have tried this method a few times on the computer and I have been up $500. Then I went to the casino and lost over $1000. Because black came up 8 times in a row. But I’m just starting to learn baccarat. I was trying it on the computer and again I have been up $500, by betting on the banker. Starting at $20 then going to $40 then $80 and so on. I was up $500 even with paying the 5%on each hand. Do you think this method would work in a casino? I thought I would ask before I go and lose another $1000. Like I said black came up 8 times in a row. But do you think that the player hand would win 8 times in a row? Plus this game is good because a tie is a push, where in roulette 0, or 00, is a loss.
The Martingale is dangerous on every game and in the long run will never win. However it is better to use in baccarat than roulette, just because of the lower house edge. The probability of the player winning 8 times in a row is 0.493163^8 = 1 in 286. Also keep in mind you could win a hand late in the series and still come out behind because of the commission. For example if you started with a bet of $1 and you won on the 7th hand you would win $60.80 ($64*95%), which would not cover the $63 in previous loses.
Hi. You say all betting systems will fail. If you play roulette and bet one unit on number 1-12 and 2 units on number 13-24 wouldn’t you then have 66.66% chance to break even or win.
Not quite. You would have a 12/38 chance of winning 3 units, 12/38 of breaking even, and 14/38 of losing 3 units. The expected value is [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5.26%. This will be true of any combination of bets as long as you avoid the dreaded 5 number combo (0/00/1/2/3). If you only play for one spin and want to maximize your probability of winning then bet equally on 35 of the numbers. You’ll have a 92.11% chance of winning 1 unit and a 7.89% chance of losing 35 units.
Hello. I’ve been an avid roulette gambler for some years now and for the first time ever I’m thinking of trying out a roulette system...Now I know how you feel about these so called "systems" and the scammers behind them, and belive me, I feel the same way, but I’ve come across two systems which can’t be ignored...
The first one is the 3q/A-strategy found in R.D Ellison’s book "Gamble to win: Roulette", which has a verified win rate of 7.94% (7500 spins). The system was tested and developed in conjunction with" Spin roultte Gold" by Frank Scoblete and "Roulette system tester" by Eric St. Germain.
The second one is Don Young’s roulette system which is verified to beat the Roulette System Tester from Zumma Publishing(15000 spins).
Now, I must say I’m still a bit sceptical about spending money on these systems, but since they've proved themselves over the long haul, I can't really see no reason why I shouldn’t. I mean, beating these testbooks have to mean something...
What’s your opinion on these systems? And do you think I should try them out??
Thanks alot! Have nice day. Best wishes
7500 spins? Is that it? Anyone can show a profit of 7.94% of total money bet over 7500 spins if they bet aggressively. Same is true about 15000 spins. Most systems are designed to have a lot of small wins and small number of large losses. A system requiring a huge bankroll can easily go 15000 spins and show a profit. Eventually the losses will come in and it won't pass the test of time. The big losses might also come at the beginning. The true way to put a system to the test is to play it over billions of trials. My opinion about these systems is the same as all systems, they are worthless. I have no problem with you trying them out but I do have a problem with anyone putting one dime in the pockets of those selling them.
Note: See the follow up to this question in the next column.
Dear Sir, In a single zero roulette game, the PROBABILTY of winning increases if you place a portion of your money on fewer numbers for more spins versus covering more numbers per spin, an example: If you are willing to risk 500$ in order to win 250$ then you could: Option (A): place 250$ on any of two dozen and should you be a winner you will win 250$. The probabilty of that happening is 24/37=(.648648). Option (B): Place 125 on any one dozen and should you be a winner you will win 250$ and walk away. However, should you lose you can now bet187.5$ on the same dozen and should you be a winner you will win 375$ which will get you the 250$ and the 125$ you lost on the previous spin. Now should you lose on both spins you still have 187.5$ to play with and you can place 20.833333$ on any nine numbers and should you be a winner you will get 750$ which is equal to your 500 original capital plus 250$ in winning which was your goal. The probability of that happening meaning either hitting a dozen OR nine numbers at LEAST once in three spin is equal to[1-(25/37)x(25/37)x(28/37)]=0.65451. Hence, for the SAME capital and for the SAME payoff you are able to increase your PROBABILITY of success as in option (B) if you play fewer numbers with less money but for MAYBE more spins.(As you might win on the first spin) You can even improve your probability further if you play only six numberes at a time and try to win 250$. Any Explanation??!!!! Assuring you of my highest regards and awaiting the favor of your reply I remain.
You are correct that option B has the greater probability of success, although the goal and the capital are the same. The reason is the average amount bet in option B is less, thus your money is exposed to the house edge less, thus the probability of winning increases. The amount bet in option A is always $500. The average amount bet in option B is (12/37)*125 + (25/37)*(12/37)*(125+187.5)+ (25/37)*(25/37)*(125+187.5+187.5) = 337.29.
When I was on the Vegas Challenge, with a few minutes to go, I had about $8,000 and needed to get to at least $24,000. So I split my bankroll into four piles of $2000 each and bet each one on a 4-number combination, each of which would have paid $22,000. This way I was not necessarily exposing my entire stake to the house edge, which increased my probability of winning.
Betting all 38 numbers on roulette would make it impossible to beat the odds even for a short time, and with a $1 bet per number there would be a loss of $2 per roll of the wheel.(0, 00 wheel, without advantageous rules for even money bets) Would it seem reasonable that there should be an optimum range of numbers to bet based on statistics?
I measure the value of a bet to be the expected return, not the probability of winning. So betting on all 38 numbers has a house edge of 2/38 = 5.26%, the same as for one number or any number of numbers covered. Although betting all 38 numbers has a 0% chance of showing a net win, the down side is losing only 5.26% of your total bets. If forced to bet and you want to minimize variance then you should bet all 38 numbers. A practical example is if you had promotional chips you had to bet and you don’t want to gamble bet get your exact expected value out of them. So to answer your question there is no optimal range of numbers. All ranges are equal in expected value.
There is a story today about a British man who will bet his life savings on one roulette roll. My friend and I have been debating about what the best casino bet is for this type of wager. If you can only place one bet, and you wish to maximize your odds, what is the best game to play and what is the best bet?
First, let me say this guy was a fool. He bet $138,000 on a normal American roulette wheel which has two zeros and a house edge of 5.26%. This amounted to an expected loss of $7,263. However had he taken a 10 minute ride to the Bellagio, Mirage, or Aladdin he could have made the bet on a single zero wheel which follows the European rule of giving half an even money bet back if the ball lands in zero. He planned to make an even money bet anyway. So, at these wheels with full European rules his house edge would have been only 1.35%, for an expected loss of only $1865.
To answer your question, if forced to make just one even money type bet I would have chosen the banker bet in baccarat with a house edge of 1.06%.
What is my risk of ruin with the following betting pattern in roulette?
Risk of ruin questions are mathematically complicated. Unless it is a simple win/lose game I would recommend doing a random simulation on a computer.
I live in NJ about two hours north of Atlantic City. Do you have an idea as to where the closest European Roulette Wheel to someone in my part of the country is?
There are lots of single zero wheels in Atlantic City. Most of the casinos there have them, but at a $25 minimum.
I was at Casino On Net. I was playing Roulette. I was making safe bets, only betting on the 1st 12(L), 2nd 12(M) & 3rd 12(H). I spun the wheel 5 times without betting, waiting for a pattern of one of the sets to not come up so I could bet on it, hoping this would shift probability of it landing in my favor. 5 spins later L didn’t show. I kept betting in L, I figured the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 OR 12 would land within 12 Spins so that I could at least recoup my money...but they didn’t. The table went 17 spins in a row without a LOW number & I went from $258 to $0.00...it was Bonus Money anyway. This is a 3 part question:
- Did my waiting for 5 spins without a low number popping actually increase the chances of probability for a L to show up?
- What are the odds that a Low number won’t show up 16 times in a row?
- What are the odds that a Low number won’t show up 17 times in a row?
Thank you, I also want to thank you for that Blackjack Guide, I turned $5.00 into $100.00 using your method.
- No
- A single-zero wheel is used at Casino on Net. So the probability of going 16 times with a zero is (25/37)16 = 0.1887%.
- (25/37)17 = 0.1275%.
What are the chances of a dealer hitting 5 of the same number in 10 spins of the roulette wheel?
The chances of any number occurring exactly 5 times in 10 spins in a double-zero roulette game could be closely approximated by 38*combin(10,5)*(1/38)5*(37/38)5 = 1 in 359275.
Congratulations on a great site. I totally understand your anger over the spread of 6 to 5 Blackjack payouts but am very curious as to why Americans seem to accept 00 Roulette without any argument. This Roulette is almost criminal and should be ranked along side Keno & Slots.
Thanks. You make a valid point. The house edge in 6 to 5 blackjack is 1.44% under the usual rules, while double zero roulette is 5.26%. That is 3.7 times as bad. However I have learned through the years that it is almost hopeless getting players to leave a game they like, regardless of how bad the house edge is. So the best I can do is advise them how to play their game of choice. For blackjack players there is still no shortage of 3 to 2 games out there. Playing 6 to 5 is giving the casino an extra 0.8% advantage for no reason at all. I also stress the importance of looking for single-zero roulette if you are a roulette player. So I see no inconsistency.
Can you please explain to me how the table limits for roulette works and what is the difference between minimum limit for individual number and table. If possible, please give examples.
There are usually two minimums in roulette. For example: $5 outside, $1 inside. Outside bets are all even money bets, column bets, and dozen bets. Inside bets are those on the numbers, including groups of 2, 3, 4, 5, and 6. In this case the minimum on outside bets is $5 and $1 on inside bets. However, you must bet at least $5 in total on inside bets or make none at all.
I work in a casino and have a bet that says a roulette dealer cannot influence the outcome of a roll. There are definitely those who think it can be done. Not to a number of course, but perhaps a section of the wheel. What would you consider a good test to reasonably determine whether a dealer has influenced the results? Assuming the number of trials is reasonable for us to attempt I will gladly share the results.
I’m on your side. If this could be done then dealers could easily conspire with players and share in the profits. Yet I never hear of this happening. A good test would be to get somebody who claims to be able to influence the roll and have him attempt to land it in a particular half of the wheel as many times as possible over 100 spins. The more times he makes it the greater weight his claim will have. The table below shows the probability of 50 to 70 successful spins. For example, the probability of 60 or more successful spins is 2.8444%. Common confidence thresholds in statistics are the 90%, 95%, and 99% levels. To beat a 90% confidence test, in which the probability of failing given random spins is 90%, the number of successful spins would need to be 57 or more. To beat a 95% test the number would need to be 59 or more, and at 99% the number would need to be 63 or more.
Probability of at Least 50 to 70Successful Roulette Spins
| Wins | Probability |
| 70 | 0.000039 |
| 69 | 0.000092 |
| 68 | 0.000204 |
| 67 | 0.000437 |
| 66 | 0.000895 |
| 65 | 0.001759 |
| 64 | 0.003319 |
| 63 | 0.006016 |
| 62 | 0.010489 |
| 61 | 0.0176 |
| 60 | 0.028444 |
| 59 | 0.044313 |
| 58 | 0.066605 |
| 57 | 0.096674 |
| 56 | 0.135627 |
| 55 | 0.184101 |
| 54 | 0.242059 |
| 53 | 0.30865 |
| 52 | 0.382177 |
| 51 | 0.460205 |
| 50 | 0.539795 |
www.ccc-casino.com has no zero roulette which they call Super Chance Roulette. Are there any systems that would be effective since there is no zero? Without the zero could one effectively play both black and red at the same time since there is no fear of the zero?
I tried to find that game but the site was down when I checked. However, assuming such a game did exist, the answer is no. No system could be expected to beat it, nor lose to it, over the long-run. The expected value of every system would be exactly zero.
Single 0 roulette. What is the probability of having any one number (0-36) come up more than once in three consecutive spins? Thanks for you time!
Regardless of what the first number is, the probability the second spin only matches it is (1/37)*(36/37). The probability only the third spin matches it is (36/37)*(1/37). The probability neither spin matches, but the second and third match each other, is (36/37)*(1/37). The probability both second and third spins match it is (1/37)*(1/37). Add up all this and you get 3*(1/37)*(36/37)+ (1/37)*(1/37) = 7.962%.
I think you may be interested in this. I use Betfair here in the UK. I am sure you nice people in America are not allowed to use it for some reason, anyway if you are not familiar with it go to betfair.co.uk and have a look. It is a betting exchange, not a bookmakers. Anyway, my question is this. They are now offering roulette with NO ZERO, yes no zero. It is genuine really. Can you think of a good strategy one could use, and if so would you keep it to yourself? Best wishes, Jonathan. P.S. They offer other casino games with no house edge too.
I tried to sign up for an account there to check this out but they block U.S. players. I’m told the minimum bet is £2 and the maximum is £50. Even in a zero house edge game like no-zero roulette there is still no betting system that will get above, or below, that 0% figure. No matter what you do the more you do of it the closer the actual house win will get to 0%.
You say there’s no winning system in roulette. Gonzalo Garcia-Pelayo and his family won a lot of money in many casinos all over the world. They even published a book, and describe how they did it. What’s your opinion?
I saw a television show about him once, and I applaud what he did. What I define as a “system” is a betting pattern, such as the Martingale, applied to a game with a house advantage, such as a fair roulette game. What Gonzalo Garcia-Pelayo successfully did was survey how often the ball landed in each number, in an effort to find, and then exploit, biased roulette wheels. This I would call a strategy, as opposed to a system. There are lots of profitable strategies for beating the casinos, but zero profitable betting systems.
If I show you a Roulette game with no zeros and all usual roulette rules apply, is it possible to win 100% of the time?
No.
I’m a long-time subscriber of your newsletter and still loving your web site. I came across a casino web site that offers roulette in which the wheel doesn’t contain any zeros. It just has number 1-36, and all the standard roulette rules apply. Do you see any way to take advantage of this? I know you don’t like betting systems but in this case there is no house edge. There must be a money management system that could work profitably with these table limits. Any advice is appreciated.
Thanks for the kind words. I think I’ve answered this one before, but no, even with zero house edge there is still no betting system that can win, over the long run.
Hello, for obvious reasons I would appreciate if you not share my name with anyone. At the casino where I work, there is virtual unanimity amongst the roulette dealers that they can "control the spin" and hit sections of the wheel with ease or miss other sections on purpose. Given all the factors in the spin of a ball in roulette, including the canoes (bumps) on the side, direction of ball and speed of wheel, etc. -- do you think there is anything to this? Would it be enough that a crooked dealer could help a player overcome the huge house advantage?
This is far from the first time I have heard this claim, and I am very skeptical of it. Most dealers also believe myths like a bad third-baseman will cause the other players to lose in blackjack, so as a group they are not the most skeptical bunch. What I think is happening is they remember the times they were successful at attempting to control the spin, and conveniently forget the times they were not. Much like they remember the times the third-baseman took the dealer’s bust card, but forget the times he saved the table.
If dealers really could do this, it would be easy to have a confederate play, causing him to win, and causing other players to lose, to make up for it. As long as they were following proper procedures for the spin, and didn’t appear with the confederate in public, it would all look completely legitimate. Yet, you never hear about this happening. I suppose the believers could say that those doing it are just keeping a low profile, but that is what believers in worthless betting systems say too. If this were as easy as the roulette dealers where you work claim, the cheating problem as a result would be rampant.
In double-zero roulette, what is the probability that any number will not have hit by the 200th spin?
The probability that any given number will not have hit is (37/38)200 = 0.48%.
With 38 numbers, we could incorrectly say that the probability that any one of them would not be hit is 38 × (37/38)200 = 18.34%.
The reason this is incorrect is it double counts two numbers not being hit. So we need to subtract those probabilities out. There are combin(38,2) = 703 sets of 2 numbers out of 38. The probability of not hitting any two given numbers is (36/38)200 = 0.000020127. We need to subtract the probability of avoiding both numbers. So we are at:
38×(37/38) 200 - combin(38,2)×(36/38) 200 = 16.9255%.
However, now we have canceled out the probability of three numbers not hitting. For any given group of three numbers, we triple counted the probability of any single number not being hit. We then triple subtracted for each way to choose two numbers out of the three, leaving with zero for the probability that all three numbers were not hit. There are combin(38,3)=8,436 such groups. Adding them back in we are now at:
38×(37/38) 200 - combin(38,2)×(36/38) 200 + combin(38,3)×(35/38)200 = 16.9862%.
Yet, now we have over-counted the probability of four numbers not hitting. For each of the combin(38,4)=73,815 groups of four numbers, each was originally quadruple counted. Then we subtracted each of the combin(4,2)=6 groups of 2 out of the 4. Then we added back in the 4 groups of 3 out of the 4. So, for each union of four numbers, it was counted 4 − 6 + 4 = 2 times. To adjust for the double counting we must subtract for each group. Subtracting them out we are now at:
38×(37/38) 200 - combin(38,2)×(36/38) 200 + combin(38,3)×(35/38)200 - combin(38,4)×(34/38)200 = 16.9845%.
Continuing in the process we would keep alternating adding and subtracting, all the way until missing 37 numbers. Thus the probability of at least one number never being hit is:
Sum i=1 to 37 [(-1)(i+1) × combin(38,i) × ((38-i)/38)38] = 16.9845715651245%
Here are the results of a random simulation of 126,900,000 such 200-spin experiments.
Numbers Hit in 200 Roulette Spins
| Numbers Hit | Observations | Ratio |
|---|---|---|
| 31 or Less | 0 | 0 |
| 32 | 1 | 0.00000001 |
| 33 | 33 | 0.00000026 |
| 34 | 1812 | 0.00001428 |
| 35 | 68845 | 0.00054251 |
| 36 | 1577029 | 0.01242734 |
| 37 | 19904109 | 0.15684877 |
| 38 | 105348171 | 0.83016683 |
| Total | 126900000 | 1 |
The ratio of times at least one number was not hit was 0.169833.
I have a friend who was part of a casino staff who watched over roulette tables, and he told me that when people start to win the casino changes the croupier. I have also seen a member of the staff ask a croupier to spin the roulette wheel at a different speed. Doesn’t this mean that the casinos are certain that the croupier can cause a non random series of numbers to appear? Doesn’t this mean that a gambler can look for a "lucky" table where the croupier doing regular spins gives them a better chance of winning?
Sadly, ignorance can go pretty high up the ladder. I don’t dispute that an expert can clock the wheel on a very slow spin. However, that issue aside, changing dealers does not change the odds. There is no such thing as a lucky or an unlucky dealer. Superstition is a difficult thing to let go of. As I have said many times, the more ridiculous a belief is, the more tenaciously it tends to be held.
Dear sir, I "clocked" an automated single-zero roulette game for 8672 games. My predetermined number came up an amazing 278 times. I chose the number because of the wear and tear of the pocket. How sure am I that this number has higher probability than 1/37?
If my terminology is correct, "clocking a wheel" means to predict where the ball will land judging by the ball speed, ball location, and wheel speed. It sounds like what you are doing is exploiting a biased wheel, which is a different advantage play. As long as we’re on the topic, a third advantage play is exploiting "dealer signature," where the croupier is so consistent that the ball and wheel speed are nearly the same every spin. This allows the player to predict where the ball will land based on ball location and past results.
To answer your question, the expected number of times you should have hit your number is 8672/37=234.38. The variance is 8672×(1/37)×(36/37)=228.04. The standard deviation is the square root of the variance, or 15.10. You had 278-234.38=43.62 more hits than expected. That is (43.62-0.5)/15.10 = 2.8556 standard deviations. The reason for subtracting 0.5 is hard to explain. Suffice it to say it is an adjustment factor for using a continuous function to estimate a discrete function. Doing a Gaussian approximation, the probability of hitting your number that many times, or more, is 0.21%. So, there is a good chance you found a biased wheel. However, there is still a 1 in 466 chance it was just good luck.
There is a well-known story about a freeze-out competition between a Japanese high roller, Kashiwagi, and Donald Trump, that took place 20 years ago. Kashiwagi was not allowed to play more than $200K per hand at baccarat. The game would be over when either the casino or the player was ahead by $12 millon. Assume that Kashiwagi always bet the maximum on Banker. What is the probability that Kashiwagi will win?
The math works out more easily if he bet on the Player. I work out a similar problem in roulette at my mathproblems.info site, problem number 116. For even money bets, the general formula is ((q/p)b-1)/((q/p)g-1), where:
b = starting bankroll in units.
g = bankroll goal in units.
p = probability of winning any given bet, not counting ties.
q = probability of losing any given bet, not counting ties.
Here the player starts with $12 million, or 60 units of $200,000, and will play until reaches 120 units or goes bust. So in the case of the Player bet the equation values are:
b = 60
g = 120
p = 0.493175
q = 0.506825
So the answer is ((0.506825/0.493175)60-1)/(( 0.506825/0.493175)120-1) = 16.27%.
It is much more complicated on the Banker bet, because of the 5% commission. That would result in the distinct possibility of the player overshooting his goal. If we add a rule that if a winning bet would cause the player to achieve his goal, he could bet only what was needed to get to $12 million exactly, then I estimate his probability of success at 21.66%.
A simpler formula for the probability of doubling a bankroll is 1/[1+(q/p)b].
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
On average, how many trials would you need in 38-number roulette before any number is repeated?
Counting the first trial, I show the mean is 8.408797, the median is 8, and the mode is 7.
The probability of two numbers without a repeat is 37/38 = 97.37%.
The probability of three numbers without a repeat is (37/38)×(36/38) = 92.24%.
The probability of four numbers without a repeat is (37/38)×(36/38)×(35/38) = 84.96%.
Following this pattern, the probability of no repeats in 8 numbers is (37/38)×(36/38)×(35/38)×...×(31/38) = 45.35%.
So the probability of a repeat within 8 numbers is 100% - 45.35% = 54.65%.
I suspect most people would estimate that that probability of a repeat within 8 numbers would be less than that. If you’re not above taking advantage of your math-challenged friends, propose a bet that it will take 8 or fewer numbers for at least one to repeat. So you would be betting on 8 or fewer, and your friend 9 or more. If he/she balks, then offer to take 7 or over, which would have a 55.59% chance of winning. Basically, whichever side covers the median of 8 is likely to win.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
The Hustling the House show on the Discovery Channel had a long segment on the best way to turn $30 into $1,000. It featured Andy Bloch saying, "If you have $30 in your pocket and you want to turn it into $1,000, then roulette is your only game." Andy went on to explain why betting the whole $30 on a single number was better than parlaying even money bets five times.
Is Andy correct in that the best way to turn $30 into $1,000 is to put the whole $30 on a single number in roulette?
No, he is not correct. The probability of Andy's single bet strategy is 1/38 = 2.6316%.
After much trial and error, I devised my "Hail Mary" roulette strategy, which will increase the odds of turning $30 into $1,000 to 2.8074%.
Wizard's "Hail Mary"strategy for roulette:
This strategy assumes that bets must be in increments of $1. In all bet calculations, round down.
Let:
b = Your bankroll
g = Your goal
- If 2*b >=g, then bet (g-b) on any even money bet.
- Otherwise, if 3*b >=g, then bet (g-b)/2 on any column.
- Otherwise, if 6*b >=g, then bet (g-b)/5 on any six line (six numbers).
- Otherwise, if 9*b >=g, then bet (g-b)/8 on any corner (four numbers).
- Otherwise, if 12*b >=g, then bet (g-b)/11 on any street (three numbers).
- Otherwise, if 18*b >=g, then bet (g-b)/17 on any split (two numbers).
- Otherwise, bet (g-b)/35 on any single number.
In other words, always try to reach the goal, with just one bet, if you can, without exceeding the goal. If there are multiple ways to accomplish this, then go with the one with the greatest probability of winning.
What about other games, you might ask? According to the Discovery Channel voice-over guy, "Everyone agrees that roulette is the best get rich quick scheme in the casino." Well, I don't. Even limiting ourselves to common games and rules, I find craps to be better. In particular, betting the don't pass and laying the odds.
Following my Hail Mary strategy for craps (explained below), the probability of turning $30 into $1,000 is 2.9244%. This assumes the player may lay 6x odds, regardless of the point (which is the case when 3x-4x-5x odds are allowed taking the odds). This probability of success is 0.117% higher than my Hail Mary strategy for roulette, and 0.2928% higher than the Andy Bloch strategy.
Andy might argue that my argument above relies on an assumption of a minimum bet of $1, which is hard to find in Vegas on a live dealer game. Expecting somebody might say that, I ran through both games under an assumption of a $5 minimum and betting in increments of $5. In that case, the probability of success using my Hail Mary strategy is 2.753% in roulette and is 2.891% in craps. In both cases, greater than the 2.632% under the Andy Bloch strategy.
In all fairness, the Discovery Channel would have never put the insane rant above on the air and was surely looking for something simple that the masses would understand. Andy was surely giving them something they wanted to hear. The basic premise of his advice is that if you want to reach a certain goal, then a hit-and-run strategy is much better than letting the house edge grind you down with multiple bets. That is definitely true and something I've been preaching for 17 years.
Wizard's "Hail Mary" strategy for craps.
This strategy assumes that bets must be in increments of $1 and wins will be rounded down to the nearest dollar. In calculating bets, never bet so much that you overshoot the goal. Also, never make a bet amount that will cause you to get rounded down.
Let:
b = Your bankroll
g = Your goal
- Bet max($1,min(b/7,(g-b)/6)) on the don't pass.
- If a point is rolled, and you have enough for a full odds bet, then lay the full odds. Otherwise, lay whatever you can.
So, I hope Andy and the Discovery Channel are happy. I've spent days running simulations to prove them wrong.
This question was raised and discussed on my forum at Wizard of Vegas.
What is the probability of the ball landing in 1, 2, and 3 within 4, 5, 6, 7, 8, or 9 spins in roulette?
The general formula is:
Pr(Ball lands in 1) +
Pr(Ball lands in 2) +
Pr(Ball lands in 3) -
Pr(Ball lands in 1 and 2) -
Pr(Ball lands in 1 and 3) -
Pr(Ball lands in 2 and 3) +
Pr(Ball lands in 1, 2, and 3).
In double-zero roulette, for n number of spins, this comes to 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n).
The following table shows the probability of rolling all three numbers for various number of spins from 3 to 100 for single- and double-zero roulette.
Roulette Question
| Spins | Single Zero |
Double Zero |
|---|---|---|
| 3 | 0.000118 | 0.000109 |
| 4 | 0.000455 | 0.000420 |
| 5 | 0.001091 | 0.001009 |
| 6 | 0.002094 | 0.001939 |
| 7 | 0.003518 | 0.003261 |
| 8 | 0.005404 | 0.005016 |
| 9 | 0.007785 | 0.007234 |
| 10 | 0.010684 | 0.009937 |
| 15 | 0.033231 | 0.031066 |
| 20 | 0.068639 | 0.064476 |
| 25 | 0.114718 | 0.108254 |
| 30 | 0.168563 | 0.159750 |
| 35 | 0.227272 | 0.216265 |
| 40 | 0.288292 | 0.275379 |
| 45 | 0.349548 | 0.335089 |
| 50 | 0.409453 | 0.393835 |
| 55 | 0.466865 | 0.450467 |
| 60 | 0.521017 | 0.504191 |
| 65 | 0.571445 | 0.554501 |
| 70 | 0.617922 | 0.601122 |
| 75 | 0.660393 | 0.643951 |
| 80 | 0.698930 | 0.683016 |
| 85 | 0.733693 | 0.718435 |
| 90 | 0.764897 | 0.750386 |
| 95 | 0.792791 | 0.779086 |
| 100 | 0.817638 | 0.804773 |
At certain casinos in Mexico they use dice instead of a wheel in roulette. Here are the rules:
- There are four dice -- two green, one red, and one blue.
- If the two green dice both land on one, then the outcome of the "spin" shall be a zero.
- If the two green dice both land on six, then the outcome of the "spin" shall be a double zero.
- If any other outcome occurs with the green dice, then the 36 possible outcomes of the red and blue dice shall be mapped to the numbers 1 and 36 to represent the "spin."
How does this change the odds compared to conventional roulette?
The probability of the 0 and 00 winning would be 1/36 each. If bets on these outcomes paid the usual 35 to 1, then the house edge would be exactly 0%.
The probability of any other number winning would be (34/36)*(1/36) = 2.62%. Compare that to 1/38=2.63% in conventional double-zero roulette. The house edge on any bet on the numbers 1 to 36 would be 5.56%. Compare that to the 5.26% in conventional double-zero roulette. My advice in this game would be to bet the zero and double-zero only.
If anyone can confirm or deny these rules and pays, please let me know.
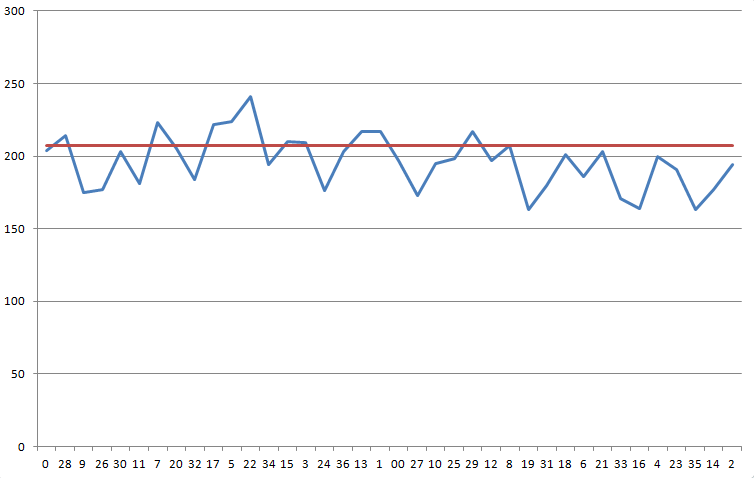
I recorded 7,456 spins in roulette. The results are as follows. I suspect the wheel is biased but am not sure if the data is conclusive enough to play it.
Roulette Data
| Winning Number |
Occurences |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Total | 7456 |
The following graph shows your results in sequential order on the wheel. The blue line shows your results. The red line is the number you need, 207.11, to overcome the 5.26% house edge.
A chi-squared test on this distribution comes back with a statistic of 68.1 with 37 degrees of freedom. The probability of a result this skewed or more is 1 in 725.
I don't think the chi-squared is the perfect test for this situation because it doesn't consider the ordering of the outcomes, but don't know of a better test. Some have suggested the Kolmogorov–Smirnov test, but I don't think that is appropriate. If there are any other appropriate tests, I'm all ears.
I can say if you had bet the 3-number arc around the number 5, you would have had a 10.57% profit over the spins you recorded. However, if you increased that to a 7-number arc, the advantage drops to 2.84%.
If forced to an answer in plain simple English, I would say the wheel shows evidence, but not proof beyond a reasonable doubt, that the wheel is biased. However, that bias is probably not enough to significantly and confidently overcome the house edge. Assuming the casino doesn't switch around the wheels among the tables, I would say that more data should be collected before betting large amounts of money. I'm sorry this answer is so noncommittal.
This question is raised and discussed in my forum at Wizard of Vegas.
In single-zero roulette, what is the mean and median number of spins required for every number to appear at least once?
Answering the mean is much easier, so we'll start with that. Let's go through it step by step:
- The first spin is definitely going to be a new number.
- The second spin will have a probability of 36/37 of being a new number. If an event has a probability of p, then the expected number of trials for it to occur is 1/p. In this case, the expected number of trials to get the second number is 37/36 = 1.0278.
- After two numbers have been observed, the probability that the next spin will result in a new number is 35/37. Thus, the expected number of spins after the second number to see the third is 37/35 = 1.0571.
- Following this logic, the average number of spins to see every number is 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155.458690.
The median is much more complicated. To find the exact answer, as opposed to using a random simulation, one needs to use a lot of matrix Algebra. I've discussed how to solve similar problems in other Ask the Wizard questions, so I won't go through the details again. One example of a similar question is the one on getting a 6-6 pair in the hole three times in a row, as discussed in Ask the Wizard #311. Suffice it to say that the probability of seeing every number in 145 spins is 0.49161779, and in 146 spins is 0.501522154. Thus, the median is 146.
This question is asked and discussed in my forum at Wizard of Vegas.
If a ball landed in red the last 20 spins in roulette, what is the probability it will land in black the next spin?
The same as red, 47.37% on a double-zero wheel, 18 black numbers divided by 38 total numbers.
I think you're wrong about the previous question. The odds of 21 reds in a row is (18/38)21 = 1 in 6,527,290. The odds must overwhelmingly favor black.
That's true, but it doesn't matter. That’s the same probability of 20 reds followed by a black. The fact is the past doesn't matter in games of independent trials like roulette.
I've thought of a way to beat the casinos in roulette! Start with a small wager on any even-money bet, like red or black. If it loses, then double the bet on the same thing. Then keeping doubling until it wins. The winning outcome has to happen eventually and when it does I'll profit my original wager. Then repeat. What is your opinion? Also, please don't tell anybody.
This is probably the most popular of all betting systems, known as the Martingale. Gamblers have been conceiving of it and using it since time immemorial. Like all betting systems, not only doesn't it beat the house advantage, it doesn't even dent it. The reason is the gambler will eventually have a bad losing streak where his bankroll isn't enough to make another double.
In your previous answer, you explained why the Martingale doesn't work. Then how about the opposite, doubling your bet after each win until a desired target is hit?
This is known as the anti-Martingale and is equally worthless. The times your bankroll gets grinded down to nothing will outweigh the winnings when you hit your target. Regardless of what betting system you use, or none at all, the more you play, the more your ratio of money lost to money bet will approach 5.26% in double-zero roulette.
What is the expected number of spins in roulette to see five reds or five blacks in a row?
What is the "law of thirds" in roulette?
The "law of thirds" says that if you spin a roulette wheel once for every number on the wheel, about 1/3 of the numbers will never occur.
1/3 is really a pretty poor estimate. A much better one would be 1/e =~ 36.79%. The true percentage, in double-zero roulette, is 36.30%.
The following table shows the probability of 1 to 38 distinct numbers being observed in 38 spins of double-zero roulette.
Law of Thirds -- Double-Zero Roulette
| Distinct Numbers |
Probability |
|---|---|
| 1 | 0.000000000 |
| 2 | 0.000000000 |
| 3 | 0.000000000 |
| 4 | 0.000000000 |
| 5 | 0.000000000 |
| 6 | 0.000000000 |
| 7 | 0.000000000 |
| 8 | 0.000000000 |
| 9 | 0.000000000 |
| 10 | 0.000000000 |
| 11 | 0.000000000 |
| 12 | 0.000000000 |
| 13 | 0.000000005 |
| 14 | 0.000000124 |
| 15 | 0.000001991 |
| 16 | 0.000022848 |
| 17 | 0.000191281 |
| 18 | 0.001186530 |
| 19 | 0.005519547 |
| 20 | 0.019434593 |
| 21 | 0.052152293 |
| 22 | 0.107159339 |
| 23 | 0.169042497 |
| 24 | 0.204864337 |
| 25 | 0.190490321 |
| 26 | 0.135436876 |
| 27 | 0.073211471 |
| 28 | 0.029838199 |
| 29 | 0.009063960 |
| 30 | 0.002020713 |
| 31 | 0.000323888 |
| 32 | 0.000036309 |
| 33 | 0.000002742 |
| 34 | 0.000000132 |
| 35 | 0.000000004 |
| 36 | 0.000000000 |
| 37 | 0.000000000 |
| 38 | 0.000000000 |
| Total | 1.000000000 |
The table shows the most likely outcome is 24 distinct numbers at 20.49%. The average is 24.20656478.
Some quacks make the argument that the player should observe the first nine distinct outcomes and then bet on them, under the incorrect belief that they are more likely to occur than other numbers. This is strictly not true! The wheel and ball do not have a memory. On a fair wheel, every number is equally likely and the past does not matter.