On this page

Video Poker (Encrypted Version)

Introduction

This page refers to a method of playing video poker using cryptography to ensure the cards dealt are predestined. If you are not familiar with the basic rules of video poker, please see my main video poker page.

For purposes of this page, I'm looking at Cypto.Games, for now. They have three versions of video poker, as follows:

  • Jacks or better
  • Tens or better
  • Bonus poker

The player must bet 10 credits, although the player may choose how much in Cryptocurrency are worth. In my opinion, the ten credits step is an unnecessarily muddying the waters.

Provably Fair Casinos

Name Wizards Seal US-OH Friendly us-oh flag Play
CryptoSlots Casino
3.8
Yes Yes Visit Casino
Name:
Wizards Seal: Yes
US-OH Friendly: Yes
Play: Visit Casino

Analysis

The following table shows my analysis of the 6-9-20-75-500 Jacks or Better pay table. The lower right cell shows a return of 97.97%, which equates to a house edge of 2.03%.

Jacks or Better Analysis

Event Pays Combinations Probability Return
Royal Flush 500 34,706,466 0.000021 0.010447
Straight Flush 75 184,178,161 0.000111 0.008316
Four of a Kind 20 3,924,486,891 0.002363 0.047252
Full House 9 19,115,939,799 0.011508 0.103572
Flush 6 19,427,500,088 0.011696 0.070173
Straight 4 18,354,238,557 0.011049 0.044198
Three of a Kind 3 123,573,760,275 0.074393 0.223178
Two Pair 2 214,462,314,819 0.129108 0.258217
Jacks or Better 1 356,047,418,052 0.214344 0.214344
All Other 0 905,977,999,992 0.545408 0.000000
Totals   1,661,102,543,100 1.000000 0.979696

The following table shows my analysis of the 5-6-22-75-500 Tens or Better pay table. The lower right cell shows a return of 97.97%, which equates to a house edge of 2.03%.

Tens or Better Analysis

Event Pays Combinations Probability Return
Royal Flush 500 38,106,048 0.000023 0.011470
Straight Flush 75 187,838,625 0.000113 0.008481
Four of a Kind 22 3,915,577,076 0.002357 0.051859
Full House 6 19,084,542,744 0.011489 0.068934
Flush 5 18,600,477,537 0.011198 0.055988
Straight 4 20,611,548,487 0.012408 0.049633
Three of a Kind 3 123,201,590,075 0.074169 0.222506
Two Pair 2 213,933,852,009 0.128790 0.257581
Tens or Better 1 420,598,763,532 0.253205 0.253205
All Other 0 840,930,246,967 0.506248 0.000000
Totals   1,661,102,543,100 1.000000 0.979657

The following table shows my analysis of the 5-8-25-35-75-45-500 Bonus Poker pay table. The lower right cell shows a return of 97.94%, which equates to a house edge of 2.06%.

Tens or Better Analysis

Event Pays Combinations Probability Return
Royal Flush 500 35,737,262 0.000022 0.010757
Straight Flush 45 172,191,438 0.000104 0.004665
Four Aces 70 325,566,459 0.000196 0.013720
Four 2s, 3s, 4s 35 875,937,305 0.000527 0.018456
Four 5s thru Ks 25 2,725,708,639 0.001641 0.041023
Full House 8 19,133,720,127 0.011519 0.092149
Flush 5 18,714,893,725 0.011267 0.056333
Straight 4 18,432,640,328 0.011097 0.044387
Three of a Kind 3 123,733,729,692 0.074489 0.223467
Two Pair 2 214,762,339,278 0.129289 0.258578
Jacks or Better 1 358,572,571,638 0.215864 0.215864
All Other 0 903,617,507,209 0.543987 0.000000
Totals   1,661,102,543,100 1.000000 0.979398

Fair Gaming

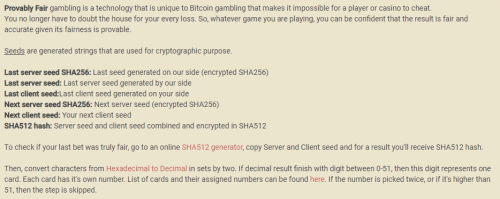
This version of video poker seems to be exclusively played at cryptocurrency Internet casinos. Briefly, the game finds ten unique random numbers from 0 to 51, each with 1/52 probability, and maps them to ten cards in the deck. The first five determine the cards the player will get on the deal and the second five the cards the player will get, in order, on the draw. For example, if the player discards two cards, then he will get the 6th and 7th card on the list on the draw. The position of the discards does not matter.

The following explanation of how cryptography is used assumes the reader has some familiarity with the concept. For the basics, please see my page on Dice (encrypted version). For the more advanced readers, here is the process of how the game chooses ten random cards.

  1. Define a pointer called "position" and set it equal to 0.
  2. Join server and client seed and server seed, in that order.
  3. Generate a SHA-512 hash of the string from step 2.
  4. Convert first two characters, starting at the "position" of the hash from step 3 from hexadecimal to decimal.
  5. Take the terminal two digits from from 4.
  6. If the result from step 5 is 51 or less, and hasn't been found yet, then that will be one of the first ten cards.
  7. Increment the "position" by 2.
  8. Keep repeating steps 4 to 7 until ten unique cards are found.
  9. The first five cards found will be dealt on the deal, starting from left to right.
  10. The second five cards will be in a queue to be dealt on the draw. For example, if the player draws three cards, then he will get the 6th, 7th, and 8th cards in the queue.
  11. To get a card position from step 6 to an actual card, do as follows:
    • A. Divide the result from step 4 by 13 and take the remainder.
    • B. Map the result from step 11A to get the rank, as follows: 0 to A, 1 to 2, 2 to 3, ... , 9 to 10, 10 to J, 11 to Q, 12 to K.
    • C. Divide the result from step 4 by 13 and DROP the remainder.
    • D. Map the result from step 11C to get the suit, as follows: 0 to spades, 1 to hearts, 2 to diamonds, 3 to clubs.

The following table shows the conversion from number to playing card.

Card Conversion Table

Rank Spades Hearts Diamonds Clubs
A 0 13 26 39
2 1 14 27 40
3 2 15 28 41
4 3 16 29 42
5 4 17 30 43
6 5 18 31 44
7 6 19 32 45
8 7 20 33 46
9 8 21 34 47
10 9 22 35 48
J 10 23 36 49
Q 11 24 37 50
K 12 25 38 51

This cries out for an example, doesn't it? Let's have one.

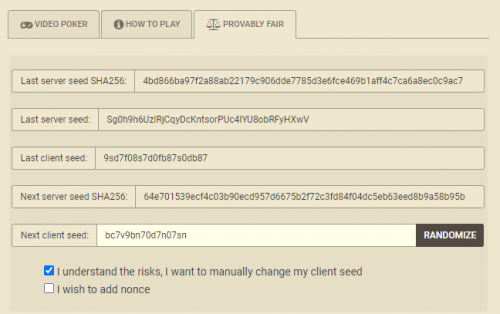
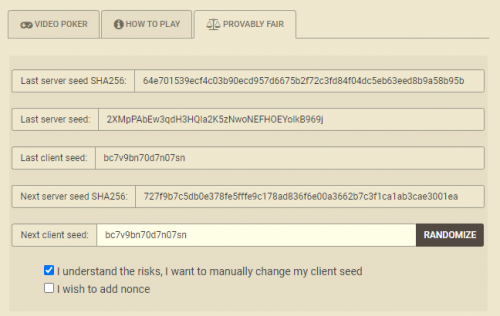
video poker crytpo games img 4

In the "Probably Fair" screen above the two important things I wish to accomplish are choose MY OWN (as opposed to the default one) Client Seed (bc7v9bn70d7n07sn), and record the Hash of the next Server Seed (64e701539ecf4c03b90ecd957d6675b2f72c3fd84f04dc5eb63eed8b9a58b95b), which is in the row titled "Next server seed SHA256.".

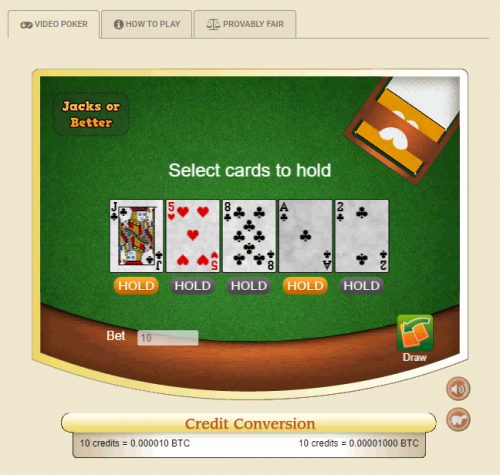
video poker crytpo games img 2

In the screen above, I hold jack/ace off-suit, in the first and fourth positions.

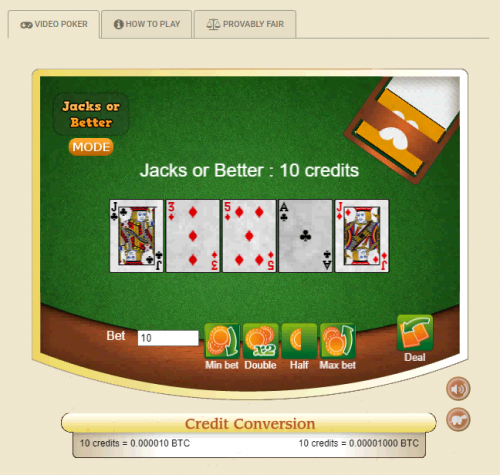
video poker crytpo games img 3

In the screen above, I improve to a pair of jacks on the draw.

video poker crytpo games img 5

In the screenshot above, I went back to the "Fair Gaming" to note how the casino takes the two Seeds to get the actual cards seen in the game.

video poker crytpo games img 4

The screen above shows what I need to know to determine what cards should have been dealt. Let me go through it step by step:

  1. The instructions are vague, but you're supposed to join the Server Seed and Client Seed, in that order. That will give you 2XMpPAbEw3qdH3HQla2K5zNwoNEFHOEYolkB969jbc7v9bn70d7n07sn.
  2. Next, take the Hash of the result of step 1. That will give you 3a959bbaffd9b3928b28431c2ee688792c67a45f1933b9e11af3c7784a7bbda5674d2e768ac330a04982b9fa943c4c2cf49c952d9db956b1cd3b38c006c3a2d6. Note that every character is a numeral from 0 to 9 or a letter from A to F. The whole thing is a very large number in hexadecimal notation.
  3. Take the first two characters in the Hash (3a) and convert them from Hexadecimal to decimal: 3*161 + a*160 = 48 + 10 = 58.
  4. Take the terminal two digits from step 3 (there are only two digits), which is still 58.
  5. If the result from step 4 is 0 to 51, map it to a card. Since 58>51, we go onto the next two digits in the Hash.
  6. The next two digits in the Hash are 95. This converts to 9*161 + 5*160 = 144 + 5 = 149 in base 10.
  7. The terminal two digits of 149 are 49, which is in the 0 to 51 range, so map it to a card. To be specific, 49 maps to the Jacks of Clubs. This shall be the first card dealt, from the left.
  8. Take the next two digits in the Hash (9b) and convert them from hexadecimal to decimal: 9*161 + b*160 = 144 + 11 = 155.
  9. Take the terminal two digits of the last step, which are 55.
  10. 55 is not in the range of 0 to 51, so skip those two digits in the Hash.
  11. Take the next two digits in the Hash (ba) and convert them from hexadecimal to decimal: b*161 + a*160 = 11*16 + 10*1 = 176 + 10 = 186.
  12. Take the terminal two digits of the last step, which are 86.
  13. 86 is not in the range of 0 to 51, so skip those two digits in the Hash.
  14. Take the next two digits in the Hash (ff) and convert them from hexadecimal to decimal: f*161 + f*160 = 15*16 + 15*1 = 240 + 15 = 255.
  15. Take the terminal two digits of the last step, which are 55.
  16. 55 is not in the range of 0 to 51, so skip those two digits in the Hash.
  17. Take the next two digits in the Hash (d9) and convert them from hexadecimal to decimal: d*161 + 9*160 = 13*16 + 9*1 = 208 + 9 = 217.
  18. Take the terminal two digits of the last step, which are 17.
  19. 17 is in the 0 to 51 range, so map it to a card. To be specific, 17 maps to the 5 of hearts. This shall be the second card dealt, from the left.
  20. Take the next two digits in the Hash (b3) and convert them from hexadecimal to decimal: 11*161 + 3*160 = 13*16 + 9*1 = 176 + 3 = 179.
  21. Take the terminal two digits of the last step, which are 79.
  22. 79 is not in the range of 0 to 51, so skip those two digits in the Hash.
  23. Take the next two digits in the Hash (92) and convert them from hexadecimal to decimal: 9*161 + 2*160 = 9*16 + 2*1 = 208 + 9 = 146.
  24. Take the terminal two digits of the last step, which are 46.
  25. 46 is in the 0 to 51 range, so map it to a card. To be specific, 46 maps to the 8 or clubs. This shall be the third card dealt, from the left.
  26. Take the next two digits in the Hash (8b) and convert them from hexadecimal to decimal: 8*161 + 11*160 = 9*16 + 2*1 = 128 + 11 = 139.
  27. Take the terminal two digits of the last step, which are 39.
  28. 39 is in the 0 to 51 range, so map it to a card. To be specific, 39 maps to the ace of clubs. This shall be the fourth card dealt, from the left.
  29. Take the next two digits in the Hash (28) and convert them from hexadecimal to decimal: 2*161 + 8*160 = 2*16 + 8*1 = 32 + 8 = 40.
  30. 40 is in the 0 to 51 range, so map it to a card. To be specific, 40 maps to the 2 of clubs. This shall be the last card on the deal, on the right.
  31. I discarded three cards, which means we need to find the next three unique cards in the Hash to replace them.
  32. Take the next two digits in the Hash (43) and convert them from hexadecimal to decimal: 4*161 + 3*160 = 4*16 + 3*1 = 67.
  33. Take the next two digits in the Hash (1c) and convert them from hexadecimal to decimal: 1*161 + c*160 = 1*16 + 12*1 = 38.
  34. 38 is in the 0 to 51 range and is unique, so map it to a card, which is the three of diamonds. This is the first card on the draw.
  35. Take the next two digits in the Hash (2e) and convert them from hexadecimal to decimal: 2*161 + e*160 = 2*16 + 14*1 = 32 + 14 = 46.
  36. 46 was also already found in the Hash, so we skip those two positions.
  37. Take the next two digits in the Hash (e6) and convert them from hexadecimal to decimal: e*161 + 6*160 = 14*16 + 6*1 = 230.
  38. Take the terminal two digits of the last step, which are 30.
  39. 30 is in the 0 to 51 range and hasn't been found yet, so map it to a card. To be specific, 30 maps to the 5 of diamonds. This shall be the second replacement card.
  40. Take the next two digits in the Hash (88) and convert them from hexadecimal to decimal: 8*161 + 8*160 = 136.
  41. Take the terminal two digits of the last step, which are 36.
  42. 36 is in the 0 to 51 range and has not been found yet, so map it to a card. To be specific, 36 maps to the jack of diamonds. This shall be the third replacement card.
  43. We don't need to find any more cards. The hand is ready to be scored and the player paid.

To summarize, the following table shows two characters at a time from the Hash, the decimal conversion, and then the card conversion, if there was one.

Hash to Card Conversion

Hash
Characters		 Decimal
Conversion		 Right Two
Digits		 Playing
Card
3a 58 58 o/r
95 49 49 Jack of clubs
9b 155 55 o/r
ba 186 86 o/r
ff 55 55 o/r
d9 217 17 5 of hearts
b3 179 79 o/r
92 146 46 8 of clubs
8b 139 39 Ace of clubs
28 40 40 2 of clubs
43 67 67 o/r
1c 28 28 3 of diamonds
2e 46 46 r/p/c
e6 230 30 5 of diamonds
88 136 36 Jack of diamonds

Key:
o/r = Decimal conversion out of range for a card
r/p/c = Repeat of previous card

If all that seems like a lot of trouble to go through to ensure a fair outcome, then I have good news for you! I wrote a script to do it for you, which is saved at the PHP Sandbox. This is a wonderful resource! To use it, just enter the Server (casino) Seed on line 4 and the Client (your own) Seed on line 5 and click Execute Code. The cards you were predestined to get will be in the results box below.

In case anything happens to the code there, you may see the code by clicking the button below.

This page refers to a method of playing video poker using cryptography to ensure the cards dealt are predestined. If you are not familiar with the basic rules of video poker, please see my main video poker page.

For purposes of this page, I'm looking at Cypto.Games, for now. They have three versions of video poker, as follows:

  • Jacks or better
  • Tens or better
  • Bonus poker

The player must bet 10 credits, although the player may choose how much in Cryptocurrency are worth. In my opinion, the ten credits step is an unnecessarily muddying the waters.

Next, click Execute Code. The cards you were predestined to get will be in the results box below as well as a verification that the Server Seed hashes to what was provided before the bet was made.

I also present a copy of the code below.

php line 1 
       // Video poker game conversion for Crypto.Games
        
$server_seed = "2XMpPAbEw3qdH3HQla2K5zNwoNEFHOEYolkB969j";
$client_seed = "bc7v9bn70d7n07sn";
$next_hash = "64e701539ecf4c03b90ecd957d6675b2f72c3fd84f04dc5eb63eed8b9a58b95b";
$rank_array=array("A",2,3,4,5,6,7,8,9,10,"J","Q","K");
$suit_array=array("spades","hearts","diamonds","clubs");
$cards_found=0;
$position=0;
$combined_seed = $server_seed.$client_seed;
echo "Combined seed = $combined_seed\n";
$combined_hash = hash('sha512', $combined_seed);
echo "Hash of combined seed = $combined_hash\n";
do
{
    $first_two=substr($combined_hash,$position,2);
    $hex_to_dec=hexdec($first_two)%100;
    if ($hex_to_dec <=51)
    {
        $repeat=0;
        if ($cards_found>0)
        {
            for ($i=0; $i<$cards_found; $i++)
            {
                if ( $hex_to_dec == $card_array[$i]) 
                { $repeat=1; }
            }
        }
        if ($repeat==0)
        {
            $card_array[$cards_found] = $hex_to_dec;
            $game_position=1+($cards_found%5);
            $cards_found++;
            $rank=$hex_to_dec%13;
            $suit=intdiv($hex_to_dec,13)%4;
            if ($cards_found<=5)
            {   echo "Deal card $game_position =\t$rank_array[$rank] of $suit_array[$suit]\n"; }
            else 
            {   echo "Draw card $game_position =\t$rank_array[$rank] of $suit_array[$suit]\n"; }
        }
    }
    $position+=2;
    if ($position==128)
    {
        echo "Error -- No more space in hash.\n";
        $cards_found=10;
    }
}
while ($cards_found<10);
$server_seed_hash = hash('sha256', $server_seed);
if ($server_seed_hash==$next_hash)
{ echo "Server Seed match.\n"; }
else
{   
    echo "SERVER SEED MISMATCH!\n";
    echo "Server seed      =\t$server_seed\n";
    echo "Server seed Hash =\t$server_seed_hash\n";
    echo "Alleged next Hash=\t$next_hash\n";
}

// Procedure
// 1.  Step the "position" to 0. 
// 2.  Join server and client seed and server seed, in that order. 
// 3.  Generate a SHA-512 hash of the string from step 2.
// 4.  Convert first two characters, starting at the "position" of the hash from step 3 from hexidecimal to decimal.
// 5.  Take the terminal two digits from from 4. 
// 6.  If the result from step 5 is 51 or less, and hasn't been found yet, then that will be one of the first ten cards.   
// 7.  Increment the "position" by 2.
// 8.  Keep repeating steps 4 to 7 until ten unique cards are found.  
// 9.  The first five cards found will be dealt on the deal, starting from left to right.
// 10. The second five cards will be in a queue to be dealt on the draw.  For example, if the player draws three cards, then he will get the 6th, 7th, and 8th cards in the queue. 
// 11  To get a card position from step 6 to an actual card, do as follows: 
//     A.  Divide the result from step 4 by 13 and take the remainder.
//     B.  Map the result from step 11A to get the rank, as follows: 0 to A, 1 to 2, 2 to 3, ... , 9 to 10, 10 to J, 11 to Q, 12 to K.
//     C.  Divide the result from step 4 by 13 and DROP the remainer.  
//     D.  Map the result from step 11C to get the suit, as follows: 0 to spades, 1 to hearts, 2 to diamonds, 3 to clubs. 
?>

Written by: Michael Shackleford