On this page
Big City 4s
Introduction
Big City 4s is a video poker variant that awards a bonus if the player gets a four of a kind on the draw. Three of a kinds and full houses on the draw vest credits into the bonus round.
Rules
- The game is based on standard multi-play video poker, which I assume the reader is familiar with.
- As usual, the game can be played in 3-, 5-, or 10-play mode.
- The player may play normally with 1 to 5 credits bet per play.
- If the player bets 6 credits per play, then he will invoke the bonus feature. This extra credit bet per play is a fee. Any wins in the base game are based on a 5-credit bet per play.
- All following rules apply only if the feature is activated.
- If the player gets certain hands, then credits will be added to the top two levels of the jackpots in the bonus round. The hands and average contribution vary by game.
- If the player gets a four of a kind on the draw, then he will play the Bonus game.
- In each level of the bonus game, the player will choose from among three cards of different ranks. The object is to pick the card highest in rank.
- The player starts on level 1.
- If the player picks the highest card in rank, then he will advance a level, up to a highest level of 4.
- If the player makes it to Level 4, then he automatically wins the Big City 4's Jackpot.
- If the player picks the middle card in rank, then that level will be replayed, until the player either advances or picks the lowest card.
- If the player picks the lowest card in rank, then the bonus shall be over. The player shall win according to the level of the bonus he achieve, as follows:
- Level 4: Big City 4's Jackpot
- Level 3: Level 3 Jackpot
- Level 2: 300 credits
- Level 1: 150 credits
- If the player gets a four of a kind and either three of a kind or full house in the same game, then the contribution to the jackpots shall be made before the bonus is played.
- The reset value for the Level 3 jackpot is 500 credits.
- The reset value for the Big City 4s jackpot is 800 credits.
- If the player gets two or more four of a kinds in the same game, then he shall play the bonus round once for each four of a kind.
If my explanation was not clear, here are the rule screens directly from the game.
Example

In the image above, I got two three of a kinds on the draw. One earned 1 credit and the other 2 credits towards the Big City 4s jackpot, as indicated in the lower left corner of the two winning hands.
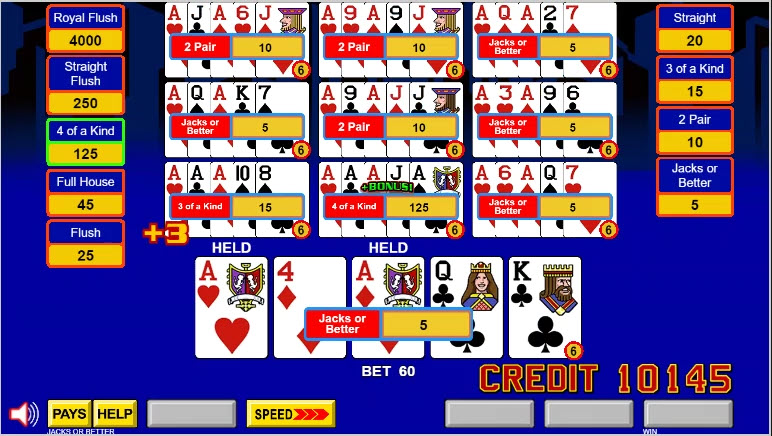
In the screen above, I got a three of a kind, which contributed 3 credits to the Big City 4s jackpot. I also got a four of a kind, which triggered the bonus, after the contribution for three of a kind was made.

The bonus starts with Round 1, in which the player tries to advance to level 2. You can see my Bonus Win is already 150, which is the least I can win.

After two pushes, I correctly pick the highest card in the middle, advancing me to Level 2, with the goal to reach Level 3. Note my bonus win is now at 300, for at least reaching level 2.

In the next level, I correctly pick the highest card on the right, advancing me to Level 3, with the goal to reach Level 4. Note my bonus win is now at 585, for at least reaching level 3./p>

In the next level, I incorrectly pick the lowest card. Having failed to reach level 4, I collect the level 3 jackpot of 585, which I did earn by passing two levels, to level 3. The Level 3 jackpot reset to 500 after that game.
Analysis
The way I analyzed Big City 4's is to assume the player plays an infinite period of time. Thus, any credits won towards the jackpots are just as valuable as if they were awarded immediately. The value of a bonus I count as 312.5 for wins based on five credits per play. That comes to 62.5 credits per credit bet per play (not counting the credit bet to invoke the feature). You can see in the tables below how I do it. The totals in the combinations column are based on an optimal strategy for the total wins shown.
The following table is for 9-5 Jacks or Better. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 9.25
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 98.66%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Jacks or Better — 9-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,307,396 | 0.000025 | 0.016578 |
| Straight flush | 50 | 0.00 | 50.00 | 163,203,492 | 0.000098 | 0.004094 |
| Four of a kind | 25 | 62.50 | 87.50 | 3,966,846,449 | 0.002388 | 0.174131 |
| Full house | 9 | 1.86 | 10.86 | 19,279,674,081 | 0.011607 | 0.105020 |
| Flush | 5 | 0.00 | 5.00 | 15,699,926,967 | 0.009452 | 0.039381 |
| Straight | 4 | 0.00 | 4.00 | 18,394,513,604 | 0.011074 | 0.036912 |
| Three of a Kind | 3 | 0.40 | 3.40 | 125,388,137,363 | 0.075485 | 0.213874 |
| Two pair | 2 | 0.00 | 2.00 | 217,109,715,255 | 0.130702 | 0.217837 |
| Jacks or better | 1 | 0.00 | 1.00 | 356,416,518,270 | 0.214566 | 0.178805 |
| Nothing | 0 | 0.00 | 0.00 | 904,642,700,223 | 0.544604 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.986632 |
The following table is for 8-5 Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 10.00
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 99.41%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Bonus Poker — 8-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,492,554 | 0.000025 | 0.016653 |
| Straight flush | 50 | 0.00 | 50.00 | 160,798,760 | 0.000097 | 0.004033 |
| Four aces | 80 | 62.50 | 142.50 | 342,047,929 | 0.000206 | 0.024453 |
| Four 2s - 4s | 40 | 62.50 | 102.50 | 889,848,106 | 0.000536 | 0.045757 |
| Four 5s-Ks | 25 | 62.50 | 87.50 | 2,746,864,166 | 0.001654 | 0.120578 |
| Full house | 8 | 2.00 | 10.00 | 19,318,576,869 | 0.011630 | 0.096916 |
| Flush | 5 | 0.00 | 5.00 | 15,543,677,781 | 0.009357 | 0.038989 |
| Straight | 4 | 0.00 | 4.00 | 18,201,198,418 | 0.010957 | 0.036524 |
| Three of a Kind | 3 | 0.40 | 3.40 | 125,818,742,158 | 0.075744 | 0.214608 |
| Two pair | 2 | 0.00 | 2.00 | 217,615,222,008 | 0.131006 | 0.218344 |
| Jacks or better | 1 | 0.00 | 1.00 | 353,377,226,154 | 0.212737 | 0.177280 |
| Nothing | 0 | 0.00 | 0.00 | 907,046,848,197 | 0.546051 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.994137 |
The following table is for 8-5 Bonus Poker Deluxe. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 8.75
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 98.56%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Bonus Poker Deluxe — 8-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,307,396 | 0.000025 | 0.016578 |
| Straight flush | 50 | 0.00 | 50.00 | 163,203,492 | 0.000098 | 0.004094 |
| Four of a kind | 25 | 62.50 | 87.50 | 3,966,846,449 | 0.002388 | 0.174131 |
| Full house | 9 | 1.75 | 10.75 | 19,279,674,081 | 0.011607 | 0.103975 |
| Flush | 5 | 0.00 | 5.00 | 15,699,926,967 | 0.009452 | 0.039381 |
| Straight | 4 | 0.00 | 4.00 | 18,394,513,604 | 0.011074 | 0.036912 |
| Three of a Kind | 3 | 0.40 | 3.40 | 125,388,137,363 | 0.075485 | 0.213874 |
| Two pair | 2 | 0.00 | 2.00 | 217,109,715,255 | 0.130702 | 0.217837 |
| Jacks or better | 1 | 0.00 | 1.00 | 356,416,518,270 | 0.214566 | 0.178805 |
| Nothing | 0 | 0.00 | 0.00 | 904,642,700,223 | 0.544604 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.985588 |
The following table is for 9-6-4 Double Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 9.29
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 96.99%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Double Bonus Poker — 9-6-4
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 39,817,188 | 0.000024 | 0.015980 |
| Straight flush | 50 | 0.00 | 50.00 | 180,863,592 | 0.000109 | 0.004537 |
| Four aces | 160 | 62.50 | 222.50 | 390,745,214 | 0.000235 | 0.043616 |
| Four 2s - 4s | 80 | 62.50 | 142.50 | 877,279,249 | 0.000528 | 0.062716 |
| Four 5s-Ks | 50 | 62.50 | 112.50 | 2,719,606,509 | 0.001637 | 0.153490 |
| Full house | 9 | 1.86 | 10.86 | 18,103,714,596 | 0.010899 | 0.098614 |
| Flush | 6 | 0.00 | 6.00 | 18,722,346,270 | 0.011271 | 0.056355 |
| Straight | 4 | 0.00 | 4.00 | 18,791,279,764 | 0.011313 | 0.037708 |
| Three of a Kind | 3 | 0.40 | 3.40 | 125,858,880,981 | 0.075768 | 0.214677 |
| Two pair | 1 | 0.00 | 1.00 | 206,090,004,807 | 0.124068 | 0.103390 |
| Jacks or better | 1 | 0.00 | 1.00 | 356,399,785,938 | 0.214556 | 0.178797 |
| Nothing | 0 | 0.00 | 0.00 | 912,928,218,992 | 0.549592 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.969880 |
The following table is for 9-6 Double Double Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 9.29
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 99.18%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Double Double Bonus Poker — 9-6
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 39,803,944 | 0.000024 | 0.015975 |
| Straight flush | 50 | 0.00 | 50.00 | 179,657,528 | 0.000108 | 0.004506 |
| Four aces + 2-4 | 400 | 62.50 | 462.50 | 102,861,693 | 0.000062 | 0.023866 |
| Four 2s - 4s + A-4 | 160 | 62.50 | 222.50 | 238,155,401 | 0.000143 | 0.026584 |
| Four aces + 5-K | 160 | 62.50 | 222.50 | 290,089,593 | 0.000175 | 0.032381 |
| Four 2s-4s + 5-K | 80 | 62.50 | 142.50 | 639,230,488 | 0.000385 | 0.045698 |
| Four 5s-Ks | 50 | 62.50 | 112.50 | 2,718,894,429 | 0.001637 | 0.153450 |
| Full house | 9 | 1.86 | 10.86 | 18,109,095,444 | 0.010902 | 0.098644 |
| Flush | 6 | 0.00 | 6.00 | 18,709,467,168 | 0.011263 | 0.056316 |
| Straight | 4 | 0.00 | 4.00 | 18,694,423,984 | 0.011254 | 0.037514 |
| Three of a Kind | 3 | 0.40 | 3.40 | 125,918,402,355 | 0.075804 | 0.214778 |
| Two pair | 1 | 0.00 | 1.00 | 206,162,927,217 | 0.124112 | 0.103427 |
| Jacks or better | 1 | 0.00 | 1.00 | 356,116,144,092 | 0.214385 | 0.178655 |
| Nothing | 0 | 0.00 | 0.00 | 913,183,389,764 | 0.549745 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.991793 |
The following table is for 8-5 Super Double Double Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 9.69
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 99.85%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Super Double Double Bonus Poker — 8-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,140,255 | 0.000025 | 0.016511 |
| Straight flush | 50 | 0.00 | 50.00 | 159,467,523 | 0.000096 | 0.004000 |
| Four aces + 2-4 | 400 | 62.50 | 462.50 | 101,231,520 | 0.000061 | 0.023488 |
| Four aces + J-K | 320 | 62.50 | 382.50 | 106,359,309 | 0.000064 | 0.020409 |
| Four 2s - 4s + A-4 | 160 | 62.50 | 222.50 | 247,268,692 | 0.000149 | 0.027601 |
| Four Js-Ks + J-A | 160 | 62.50 | 222.50 | 283,428,433 | 0.000171 | 0.031637 |
| Four aces + 5-K | 160 | 62.50 | 222.50 | 186,848,257 | 0.000112 | 0.020856 |
| Four 2s-4s + 5-K | 80 | 62.50 | 142.50 | 666,543,873 | 0.000401 | 0.047650 |
| Four 5s-Ks | 50 | 62.50 | 112.50 | 2,445,082,559 | 0.001472 | 0.137997 |
| Full house | 8 | 1.94 | 9.94 | 17,690,369,055 | 0.010650 | 0.088198 |
| Flush | 5 | 0.00 | 5.00 | 16,453,342,652 | 0.009905 | 0.041271 |
| Straight | 4 | 0.00 | 4.00 | 18,039,964,586 | 0.010860 | 0.036201 |
| Three of a Kind | 3 | 0.40 | 3.40 | 127,520,508,137 | 0.076769 | 0.217511 |
| Two pair | 1 | 0.00 | 1.00 | 207,899,626,869 | 0.125158 | 0.104298 |
| Jacks or better | 1 | 0.00 | 1.00 | 360,590,565,207 | 0.217079 | 0.180899 |
| Nothing | 0 | 0.00 | 0.00 | 908,670,796,173 | 0.547029 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.998528 |
The following table is for 8-5 Super Double Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 8.75
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 99.85%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Super Double Bonus Poker — 8-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,140,556 | 0.000025 | 0.016511 |
| Straight flush | 80 | 0.00 | 80.00 | 185,457,798 | 0.000112 | 0.007443 |
| Four aces | 160 | 62.50 | 222.50 | 380,518,438 | 0.000229 | 0.042474 |
| Four Js-Ks | 120 | 62.50 | 182.50 | 1,087,042,494 | 0.000654 | 0.099525 |
| Four 2s-4s | 80 | 62.50 | 142.50 | 887,406,566 | 0.000534 | 0.063440 |
| Four 5s-10s | 50 | 62.50 | 112.50 | 1,757,600,963 | 0.001058 | 0.099196 |
| Full house | 8 | 1.75 | 9.75 | 15,380,404,497 | 0.009259 | 0.075231 |
| Flush | 5 | 0.00 | 5.00 | 17,272,847,746 | 0.010398 | 0.043327 |
| Straight | 4 | 0.00 | 4.00 | 18,634,725,622 | 0.011218 | 0.037394 |
| Three of a Kind | 3 | 0.40 | 3.40 | 130,552,617,404 | 0.078594 | 0.222683 |
| Two pair | 1 | 0.00 | 1.00 | 184,286,171,322 | 0.110942 | 0.092452 |
| Jacks or better | 1 | 0.00 | 1.00 | 379,142,907,123 | 0.228248 | 0.190206 |
| Nothing | 0 | 0.00 | 0.00 | 911,493,702,571 | 0.548728 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.989882 |
The following table is for 9-6 Triple Double Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 8.75
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 98.38%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Triple Double Bonus Poker — 9-6
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 39,661,855 | 0.000024 | 0.015918 |
| Straight flush | 50 | 0.00 | 50.00 | 177,578,086 | 0.000107 | 0.004454 |
| Four aces + 2-4 | 800 | 62.50 | 862.50 | 117,128,451 | 0.000071 | 0.050681 |
| Four 2s - 4s + A-4 | 400 | 62.50 | 462.50 | 287,437,500 | 0.000173 | 0.066693 |
| Four aces + 5-K | 160 | 62.50 | 222.50 | 248,547,376 | 0.000150 | 0.027744 |
| Four 2s-4s + 5-K | 80 | 62.50 | 142.50 | 534,210,327 | 0.000322 | 0.038190 |
| Four 5s-Ks | 50 | 62.50 | 112.50 | 2,714,134,028 | 0.001634 | 0.153181 |
| Full house | 9 | 2.14 | 11.14 | 17,575,595,046 | 0.010581 | 0.098242 |
| Flush | 6 | 0.00 | 6.00 | 18,463,806,574 | 0.011115 | 0.055577 |
| Straight | 4 | 0.00 | 4.00 | 20,867,991,643 | 0.012563 | 0.041876 |
| Three of a Kind | 2 | 0.40 | 2.40 | 126,085,271,079 | 0.075905 | 0.151809 |
| Two pair | 1 | 0.00 | 1.00 | 205,077,698,721 | 0.123459 | 0.102882 |
| Jacks or better | 1 | 0.00 | 1.00 | 351,859,979,496 | 0.211823 | 0.176519 |
| Nothing | 0 | 0.00 | 0.00 | 917,053,502,918 | 0.552075 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.983766 |
The following table is for 9-5 Triple Triple Bonus Poker. For a max bet, the game awards average bonus contributions as follows:
- Three of a kind — 2.00
- Full house — 11.25
All wins in the table are relative to each credit bet per play, assuming a max bet. The lower right cell shows a return to player of 98.86%. This was calculated as the product of the total win, probability, and 5/6. The reason for multiplying by 5/6, is the player must pay 1/6 of his total bet as a fee to invoke the feature.
Triple Triple Bonus Poker — 9-5
| Hand | Base Win |
Feature Win |
Total Win |
Combinations | Probability | Return |
|---|---|---|---|---|---|---|
| Royal flush | 800 | 0.00 | 800.00 | 41,491,049 | 0.000025 | 0.016652 |
| Straight flush | 50 | 0.00 | 50.00 | 167,002,155 | 0.000101 | 0.004189 |
| Four aces + 2-4 | 800 | 62.50 | 862.50 | 118,201,642 | 0.000071 | 0.051145 |
| Four 2s - 4s + A | 800 | 62.50 | 862.50 | 139,730,980 | 0.000084 | 0.060461 |
| Four 2s - 4s + 2-4 | 400 | 62.50 | 462.50 | 134,327,056 | 0.000081 | 0.031167 |
| Four aces + 5-K | 160 | 62.50 | 222.50 | 251,988,282 | 0.000152 | 0.028128 |
| Four 2s-4s + 5-K | 80 | 62.50 | 142.50 | 535,954,292 | 0.000323 | 0.038315 |
| Four 5s-Ks | 50 | 62.50 | 112.50 | 2,722,196,227 | 0.001639 | 0.153636 |
| Full house | 9 | 2.25 | 11.25 | 17,614,730,679 | 0.010604 | 0.099415 |
| Flush | 5 | 0.00 | 5.00 | 17,029,580,836 | 0.010252 | 0.042717 |
| Straight | 3 | 0.00 | 3.00 | 16,844,625,732 | 0.010141 | 0.025352 |
| Three of a Kind | 2 | 0.40 | 2.40 | 126,084,344,859 | 0.075904 | 0.151808 |
| Two pair | 1 | 0.00 | 1.00 | 208,556,865,099 | 0.125553 | 0.104628 |
| Jacks or better | 1 | 0.00 | 1.00 | 360,710,934,075 | 0.217152 | 0.180960 |
| Nothing | 0 | 0.00 | 0.00 | 910,150,570,137 | 0.547920 | 0.000000 |
| Total | 1,661,102,543,100 | 1.000000 | 0.988571 |
There are also deuces wild and joker poker games available for Big City 4s. For purposes of progressive contributions and triggering the bonus, deuces and the joker are not wild. I have no analyzed these games yet, so you're on your own there.
To create a strategy for any game without wild cards, first go to my Video Poker Strategy Maker. Then, add to the full 5-coin wins whatever the average contribution is for a three of a kind and full house. For all four of a kind wins, add 312.5. That will generate the approriate strategy for that game.
Return Summary
The following table shows the games available at VideoPoker.com, average progressive contributions, and return. These are most likely the most liberal pay tables available for Big City 4s.
Summary
| Game | Pay Table | Three of a Kind Contribution |
Full House Contribution |
Return |
|---|---|---|---|---|
| Jacks or Better | 9-5 | 2.00 | 9.29 | 98.66% |
| Bonus Poker | 8-5 | 2.00 | 10.00 | 99.41% |
| Bonus Poker Deluxe | 8-5 | 2.00 | 8.75 | 98.56% |
| Double Bonus | 9-6 | 2.00 | 9.29 | 96.99% |
| Double Double Bonus | 9-6 | 2.00 | 9.29 | 99.18% |
| Super Double Double | 8-5 | 2.00 | 9.69 | 99.85% |
| Super Double Bonus | 8-5 | 2.00 | 8.75 | 98.99% |
| Triple Double Bonus | 9-6 | 2.00 | 10.71 | 98.38% |
| Triple Triple Bonus | 9-5 | 2.00 | 11.25 | 98.86% |
| Deuces Wild | 25-15-9-4-4-3-2 | 2.00 | 2.50 | ? |
| Deuces Wild Bonus | 25-13-9-4-3-3 | 1.00 | 1.00 | ? |
| Joker Poker (kings or better) | 16-7-5-3-2 | 1.50 | 8.00 | ? |
| Joker Poker (two pair or better) | 16-8-5-4-2 | 1.50 | 8.00 | ? |
Vulturing
Any game with a progressive turns positive at some point, including this game (shut up, Wiz!). To find the breakeven point, the sum of the top two jackpots, for any game that doesn't involve wild cards, can be easily approximated as, 21300 - 20000r, where r = the return to player. For every 100 credits above that point, combined between the two jackpots, the return goes up by 0.5%.
The following table shows the breakeven point for the non-wild-card games shown in this page.
Breakeven Points
| Game | Pay Table | Return | Breakeven Point |
|---|---|---|---|
| Jacks or Better | 9-5 | 98.66% | 1569 |
| Bonus Poker | 8-5 | 99.41% | 1417 |
| Bonus Poker Deluxe | 8-5 | 98.56% | 1590 |
| Double Bonus | 9-6 | 96.99% | 1902 |
| Double Double Bonus | 9-6 | 99.18% | 1464 |
| Super Double Double | 8-5 | 99.85% | 1329 |
| Super Double Bonus | 8-5 | 98.99% | 1496 |
| Triple Double Bonus | 9-6 | 98.38% | 1632 |
| Triple Triple Bonus | 9-5 | 98.86% | 1534 |
External Links
- VideoPoker.com — Play Big City 4s for fun. A Gold level membership is required for this game.
- Discussion about Big City 4s in my forum at Wizard of Vegas.


