Super Hot Roll

Introduction

I first noticed Super Hot Roll at the Red Rock casino in Las Vegas on May 3, 2021. It is a variation of the game Hot Roll, adding a feature where multipliers apply to both the current game and the next one.

Rules

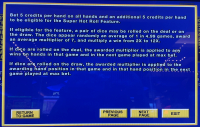
1. Super Hot Roll is an optional feature added to 3-, 5-, and 10-play video poker.
2. If the player bets one to five coins per hand, then the feature is not activated and the game plays like conventional multi-play video poker.
3. If the player bets ten coins per hand, then the feature will be enabled. Wins will be based on a five coin bet per hand. The other five coins bet per hand is a fee to pay for the feature.
4. If the feature is enabled, then randomly, with a 1 in 4.99 chance, the player will earn a multiplier.
5. The multiplier shall be determined by the total of two six-sided dice.
6. Usually, the multiplier shall be awarded on the draw and applied to one hand only. Sometimes, and I don't know how often, the multiplier will be awarded on the deal and apply to all hands.
7. After the draw, wins shall be evaluated including any multipliers for that game. Then, any multipliers earned that hand shall be carried over to the same positions in the next hand.
8. If the player earns a multiplier for a hand that already had one from the previous game, then for that hand the player shall keep the multiplier from the previous game. The subsequent multiplier shall apply to the next game only.

If my explanation of the rules was unclear, here are the help screens from the game. Click on any image for a larger version.

Example

In the image above, I was dealt four to a flush.

I held the four spades. After clicking draw, the lower hand was awarded a multiplier. The dice were rolled for a total of 11. This gave me a multiplier of 11 for the bottom hand only for the current hand and the next one.

The image above scored the current hand. Unfortunately, all three hands lost. Had the bottom hand won anything, the win would have been multiplied by 11.

The image above shows the next hand. The bottom hand is shown to have a multiplier of 11, earned the previous hand. I choose to hold the king only.

The image above shows the draw. The top hand improved to a straight. The middle hand improved to a three of a kind. The bottom hand, with the 11x multiplier, improved to a pair of kings. The bottom hand also triggered the multiplier feature. The roll of the dice was an 8. Since I already had a multiplier for that hand, the additional multiplier didn't help for the current hand. However, it will carry over to the next hand in that position.

The image above shows the scoring of the last hand. The top had was a straight, which pays 4 for 1. The middle hand was a three of a kind, which pays 3 for 1. The bottom hand was "jacks or better," which pays 11 for 1, after applying the 11x multiplier. Based on the 5 credits bet per hand, the total win is 5×(4 + 3 + 11) = 90.

The image above shows the next hand. I choose to hold the pair of tens. Note the bottom hand has an 8x multiplier, earned the previous hand.

The image above shows the outcome of the draw. Unfortunately, none of the hands improved. My 8x multiplier was wasted.

Analysis

As mentioned in the rules, the game mysteriously sometimes awards a multiplier to all three hands and sometimes to one only. It does not disclose the probability either way. Without that information, I can't do a proper analysis.

I will say it is very typical of games with an optional feature to multi-play video poker that enabling the feature results in a slight boost in the expected return.