On this page
Stack 'em High Poker
Introduction
One video poker variant I saw at G2E and now at VideoPoker.com is Stack 'em High Poker.
The thrust of the game is if the player invokes the feature, by doubling his bet, then if he is dealt two or three aces then he will get extra hands on the draw and any new aces dealt will be "sticky" for the rest of the hands not dealt to yet.
Rules
- Game is an optional feature on 3-play and 5-play video poker.
- The player must play 10 credits per line to invoke the feature. Wins will be based on 5 credits only. If the player is dealt 2 or 3 aces, then he will Bonus Hands. The number of Bonus Hands includes the hands the player already paid for.
- The number of Bonus Hands is disclosed in the rules. For example, the most liberal version of Bonus Poker awards 12 Bonus Hands for two aces and 13 for three aces.
- Regardless of how many hands the player has, they will be in the form of a vertical stack.
- Replacements cards are dealt to one hand at a time, starting at the bottom of the stack. If the player is dealt any additional aces on the draw, those aces will be sticky for all hands above.
- To invoke the feature, the player must hold the 2 or 3 dealt aces only. If the holds other cards, he won't get the bonus hands.
- In the bonus feature, every hand on the draw is dealt from a 52-card with the five cards from the deal removed and any "sticky" aces from previous hands drawn.
- If the player doubles his bet to enable the feature, there will often be a pay table boost. For example, in what is normally 8-5 Bonus Poker for one to five coins bet, the pay table is boosted to 10-7 if the player pays for the feature.
Example
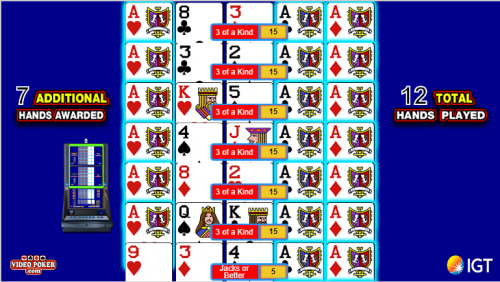
In this screen I was awarded two aces on the deal, which I held. Please note this screenshot was taken when VideoPoker.com was incorrectly not giving the player the pay table boost for playing the feature.
The next screen shows my first five Bonus Hands, none of which improved beyond the pair of aces.
The next screen shows the seven additional Bonus Hands. Note the second from the bottom was dealt the ace of hearts in the left position. This ace was cloned to every hand above it. However, none of them improved above that three of a kind.
Return Table
The following table lists the games, pay tables, stack sizes, and returns that I am aware of for 5-play Stack 'em High. These are the most liberal pay tables available. There are less-generous pay tables out there, but I don't know what they are.
Stack 'em High -- 5 Play
| Game | Pay Table | Bonus Games* | Return |
|---|---|---|---|
| Triple Triple Bonus | 9-6 | 2,5 | 98.67% |
| Double Double Bonus | 10-7-5 | 3,6 | 99.36% |
| Triple Double Bonus | 11-6 | 2,5 | 99.04% |
| Double Bonus | 11-7 | 4,8 | 99.10% |
| Bonus Poker | 10-7 | 7,8 | 99.42% |
| White Hot Aces | 9-6 | 3,4 | 99.19% |
| Triple Bonus | 9-6 | 3,4 | 99.31% |
| Super Double Double Bonus | 8-5 | 3,2 | 99.55% |
| Super Double Bonus | 9-6-5 | 4,8 | 99.44% |
| Deuces Wild | 16-14-4-4-3 | 3,8 | 99.24% |
| Deuces Wild Bonus | 11-4-3-3 | 3,6 | 98.21% |
| Loose Deuces Wild | 17-13-4-3 | 1,2 | 99.11% |
| Double Deuces | 16-12 | 3,6 | 99.06% |
The following table lists the games, pay tables, stack sizes, and returns that I am aware of for 3-play Stack 'em High. These are the most liberal pay tables available. There are less-generous pay tables out there, but I don't know what they are.
Stack 'em High — 3 Play
| Game | Pay Table | Bonus Games* | Return |
|---|---|---|---|
| Triple Triple Bonus | 9-6 | 3,2 | 99.35% |
| Double Double Bonus | 10-8-6 | 3,5 | 99.14% |
| Triple Double Bonus | 9-7 | 3,2 | 99.28% |
| Double Bonus | 11-7-5 | 4,8 | 99.12% |
| Bonus Poker | 10-8-6 | 6,9 | 99.41% |
| White Hot Aces | 10-7-5 | 3,6 | 99.38% |
| Triple Bonus | 10-7-5 | 3,6 | 99.51% |
| Super Double Double Bonus | 8-6-5 | 3,5 | 99.14% |
| Super Double Bonus | 9-6-5 | 4,8 | 99.14% |
| Deuces Wild | 15-12-5-5-4 | 3,6 | 99.08% |
| Deuces Wild Bonus | 13-4-3-3 | 3,7 | 98.25% |
| Double Bonus Deuces Wild | 12-4-3 | 3,7 | 98.82% |
| Loose Deuces Wild | 15-10-4-3 | 2,1 | 99.44% |
| Double Deuces | 15-11-5 | 3,6 | 99.38% |
*: The Bonus Games column shows the number of total games for two aces as the first number and the number of games for three aces as the second number.
Analysis
Following is my analysis of 5-play 10-7 Bonus Poker. As a reminder, the game awards 12 bonus hands for two dealt aces and 13 for three. When the player invokes the feature, there is a pay table boost from 8-5 to 10-5.
The following table shows the probability of all possible outcomes of the 12 bonus hands after two dealt aces, assuming the player discards three singletons.
Bonus Hand Probabilities for Two Aces (Discarding Three Singletons)
| Hand | Two Aces | Two Pair | Three Aces | Full House (two aces) |
Full House (three aces) |
Four Aces |
|---|---|---|---|---|---|---|
| 1 | 0.712858 | 0.159852 | 0.114339 | 0.002405 | 0.007771 | 0.002775 |
| 2 | 0.623834 | 0.139889 | 0.100059 | 0.002105 | 0.006800 | 0.002429 |
| 3 | 0.545927 | 0.122419 | 0.087564 | 0.001842 | 0.005951 | 0.002125 |
| 4 | 0.477749 | 0.107131 | 0.076628 | 0.001612 | 0.005208 | 0.001860 |
| 5 | 0.418085 | 0.093752 | 0.067059 | 0.001411 | 0.004557 | 0.001628 |
| 6 | 0.365873 | 0.082044 | 0.058684 | 0.001234 | 0.003988 | 0.001424 |
| 7 | 0.320181 | 0.071798 | 0.051355 | 0.001080 | 0.003490 | 0.001246 |
| 8 | 0.280196 | 0.062831 | 0.044942 | 0.000945 | 0.003054 | 0.001091 |
| 9 | 0.245204 | 0.054985 | 0.039329 | 0.000827 | 0.002673 | 0.000955 |
| 10 | 0.214582 | 0.048118 | 0.034418 | 0.000724 | 0.002339 | 0.000835 |
| 11 | 0.187784 | 0.042109 | 0.030119 | 0.000634 | 0.002047 | 0.000731 |
| 12 | 0.164332 | 0.036850 | 0.026358 | 0.000554 | 0.001791 | 0.000640 |
By the end of the bonus, the player can expect to have won 4.556604 high pairs, 1.021777 two pairs, 4.917541 three of a kinds, 0.349576 full houses, and 1.154503 four aces. The average bonus win for getting two aces and three singletons is 1×4.556604 + 2×1.021777 + 3×4.917541 + 10×0.349576 + 80×1.154503 = 117.208750.
The following table shows the probability of all possible outcomes of the 12 bonus hands after two dealt aces, assuming the player discards another pair and a singleton.
Bonus Hand Probabilities for Two Aces (Discarding a Pair and a Singleton)
| Hand | Two Aces | Two Pair | Three Aces | Full House (two aces) |
Full House (three aces) |
Four Aces |
|---|---|---|---|---|---|---|
| 1 | 0.710453 | 0.162134 | 0.114215 | 0.002529 | 0.007894 | 0.002775 |
| 2 | 0.621729 | 0.141886 | 0.099952 | 0.002213 | 0.006908 | 0.002429 |
| 3 | 0.544085 | 0.124167 | 0.087469 | 0.001936 | 0.006045 | 0.002125 |
| 4 | 0.476137 | 0.108660 | 0.076546 | 0.001695 | 0.005290 | 0.001860 |
| 5 | 0.416675 | 0.095090 | 0.066986 | 0.001483 | 0.004630 | 0.001628 |
| 6 | 0.364639 | 0.083215 | 0.058621 | 0.001298 | 0.004052 | 0.001424 |
| 7 | 0.319101 | 0.072823 | 0.051300 | 0.001136 | 0.003546 | 0.001246 |
| 8 | 0.279250 | 0.063728 | 0.044893 | 0.000994 | 0.003103 | 0.001091 |
| 9 | 0.244376 | 0.055770 | 0.039287 | 0.000870 | 0.002715 | 0.000955 |
| 10 | 0.213858 | 0.048805 | 0.034381 | 0.000761 | 0.002376 | 0.000835 |
| 11 | 0.187150 | 0.042710 | 0.030087 | 0.000666 | 0.002079 | 0.000731 |
| 12 | 0.163778 | 0.037376 | 0.026330 | 0.000583 | 0.001820 | 0.000640 |
By the end of the bonus, the player can expect to have won 4.541230 high pairs, 1.036362 two pairs, 4.912236 three of a kinds, 0.355669 full houses, and 1.154503 four aces. The average bonus win for getting two aces and three singletons is 1×4.541230 + 2×1.036362 + 3×4.912236 + 10×0.355669 + 80×1.154503 = 117.267565.
The following table shows the probability of all possible outcomes of the 12 bonus hands after two dealt aces, assuming the player discards a three of a kind.
Bonus Hand Probabilities for Two Aces (Discarding a Three of a Kind)
| Hand | Two Aces | Two Pair | Three Aces | Full House (two aces) |
Full House (three aces) |
Four Aces |
|---|---|---|---|---|---|---|
| 1 | 0.705520 | 0.166883 | 0.113969 | 0.002714 | 0.008141 | 0.002775 |
| 2 | 0.617411 | 0.146041 | 0.099736 | 0.002375 | 0.007124 | 0.002429 |
| 3 | 0.540306 | 0.127803 | 0.087280 | 0.002078 | 0.006234 | 0.002125 |
| 4 | 0.472830 | 0.111843 | 0.076380 | 0.001819 | 0.005456 | 0.001860 |
| 5 | 0.413781 | 0.097875 | 0.066842 | 0.001591 | 0.004774 | 0.001628 |
| 6 | 0.362106 | 0.085652 | 0.058494 | 0.001393 | 0.004178 | 0.001424 |
| 7 | 0.316885 | 0.074955 | 0.051189 | 0.001219 | 0.003656 | 0.001246 |
| 8 | 0.277311 | 0.065595 | 0.044796 | 0.001067 | 0.003200 | 0.001091 |
| 9 | 0.242679 | 0.057403 | 0.039202 | 0.000933 | 0.002800 | 0.000955 |
| 10 | 0.212372 | 0.050234 | 0.034306 | 0.000817 | 0.002450 | 0.000835 |
| 11 | 0.185850 | 0.043961 | 0.030022 | 0.000715 | 0.002144 | 0.000731 |
| 12 | 0.162641 | 0.038471 | 0.026273 | 0.000626 | 0.001877 | 0.000640 |
By the end of the bonus, starting with two aces and a discarded three of a kind, the player can expect to have won 4.509694 high pairs, 1.066716 two pairs, 4.901626 three of a kinds, 0.367461 full houses, and 1.154503 four aces. The average bonus win for getting two aces and three singletons is 1×4.509694 + 2×1.066716 + 3×4.901626 + 10×0.367461 + 80×1.154503 = 117.2200063.
The following table shows the probability of all possible outcomes of the 13 bonus hands after three dealt aces, assuming the player discards two singletons.
Bonus Hand Probabilities for Three Aces (Discarding Two Singletons)
| Hand | Three Aces | Full House | Four Aces |
|---|---|---|---|
| 1 | 0.896392 | 0.061055 | 0.042553 |
| 2 | 0.858248 | 0.058457 | 0.083296 |
| 3 | 0.821727 | 0.055969 | 0.122304 |
| 4 | 0.786760 | 0.053587 | 0.159653 |
| 5 | 0.753280 | 0.051307 | 0.195413 |
| 6 | 0.721226 | 0.049124 | 0.229650 |
| 7 | 0.690536 | 0.047033 | 0.262431 |
| 8 | 0.661151 | 0.045032 | 0.293817 |
| 9 | 0.633017 | 0.043116 | 0.323867 |
| 10 | 0.606080 | 0.041281 | 0.352639 |
| 11 | 0.580289 | 0.039524 | 0.380186 |
| 12 | 0.555596 | 0.037842 | 0.406561 |
| 13 | 0.531954 | 0.036232 | 0.431814 |
By the end of the bonus, starting with three aces and two singletons, the player can expect to have won 9.096256 three of a kinds, 0.619559 full houses, and 3.284185 four aces. The average bonus win for getting two aces and three singletons is 3×9.096256 + 10×0.619559 + 80×3.284185 = 296.219154.
The following table shows the probability of all possible outcomes of the 13 bonus hands after three dealt aces, assuming the player discards a pair.
Bonus Hand Probabilities for Three Aces (Discarding a Pair)
| Hand | Three Aces | Full House | Four Aces |
|---|---|---|---|
| 1 | 0.895467 | 0.061980 | 0.042553 |
| 2 | 0.857362 | 0.059342 | 0.083296 |
| 3 | 0.820879 | 0.056817 | 0.122304 |
| 4 | 0.785948 | 0.054399 | 0.159653 |
| 5 | 0.752503 | 0.052084 | 0.195413 |
| 6 | 0.720482 | 0.049868 | 0.229650 |
| 7 | 0.689823 | 0.047746 | 0.262431 |
| 8 | 0.660469 | 0.045714 | 0.293817 |
| 9 | 0.632364 | 0.043769 | 0.323867 |
| 10 | 0.605455 | 0.041906 | 0.352639 |
| 11 | 0.579691 | 0.040123 | 0.380186 |
| 12 | 0.555023 | 0.038416 | 0.406561 |
| 13 | 0.531405 | 0.036781 | 0.431814 |
By the end of the bonus, starting with three aces and discarded pair, the player can expect to have won 9.086869 three of a kinds, 0.619559 0.628946, and 3.284185 four aces. The average bonus win for getting two aces and three singletons is 1×4.509694 + 2×1.066716 + 3×9.086869 + 10×0.628946 + 80×3.284185 = 296.2233478.
The next table shows the expected return after the draw in 10-5 Bonus Poker when the player has 0, 1, or 4 aces on the deal. The lower right cell shows that when the player has 0, 1 or 4 aces on the deal, he can expect a return of 94.53%.
10-7 Bonus Poker with 0, 1, or 4 Aces on the Deal
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | 800 | 407,220,072 | 0.000021 | 0.017054 |
| Straight flush | 50 | 2,165,260,068 | 0.000113 | 0.005667 |
| Four aces | 80 | 664,739,580 | 0.000035 | 0.002784 |
| Four 2-4 | 40 | 10,499,553,552 | 0.000550 | 0.021985 |
| Four 5-K | 25 | 32,463,889,224 | 0.001699 | 0.042486 |
| Full house | 10 | 202,070,667,924 | 0.010578 | 0.105781 |
| Flush | 7 | 290,934,586,020 | 0.015230 | 0.106610 |
| Straight | 4 | 217,043,262,036 | 0.011362 | 0.045448 |
| Three of a kind | 3 | 1,363,205,170,488 | 0.071362 | 0.214086 |
| Two pair | 2 | 2,305,997,183,808 | 0.120716 | 0.241432 |
| Jacks or better | 1 | 3,581,309,420,208 | 0.187477 | 0.187477 |
| Nothing | 0 | 11,095,933,632,060 | 0.580857 | 0.000000 |
| Total | 19,102,694,585,040 | 1.000000 | 0.990810 |
The final table in this analysis of 10-7 Bonus Poker brings everything together by the hand on the deal. Wins are expressed based on five hands bet. The return column is the product of the win, probability, and 0.1. The reason for dividing by 10 is because the player must bet 10 coins per hand. The lower right cell shows an overall return of the game of 99.42%.
10-7 Bonus Poker Return with Feature
| Deal | Combinations | Probability | Avg. Win | Exp. Win |
|---|---|---|---|---|
| 0, 1, or 4 aces on deal | 2,490,672 | 0.958334 | 4.954049 | 0.474763 |
| Two aces and three singletons on deal | 84,480 | 0.032505 | 117.208750 | 0.380991 |
| Two aces another pair and a singleton on deal | 19,008 | 0.007314 | 117.267565 | 0.085766 |
| Two aces and three of a kind on deal | 288 | 0.000111 | 117.382829 | 0.001301 |
| Three aces and two singletons on deal | 4,224 | 0.001625 | 296.219154 | 0.048143 |
| Three aces and pair on deal | 288 | 0.000111 | 296.284864 | 0.003283 |
| Total | 2,598,960 | 1.000000 | 0.994248 |
Acknowledgements
I would like to thanks VideoPoker.com for letting me use screenshots from their web site and the return tables seen in this page.