On this page
Extreme X Poker
Introduction
Extreme X Poker is a video poker variant by IGT that features a multiplier-based bonus after any full house or better on the draw. Once in the bonus, the player has five "Fever Games" to accept the multiplier. It makes for interesting strategy whether to accept it on a marginal win or try for a bigger win to apply it before the five Fever Games are over.
Rules
- Extreme X Poker plays like conventional single-line video poker for one to five coins bet.
- For an optional sixth coin bet, the player enables the bonus feature. This sixth coin is generally a fee and does not directly increase the wins. However, on some games, it does bump up some wins a little.
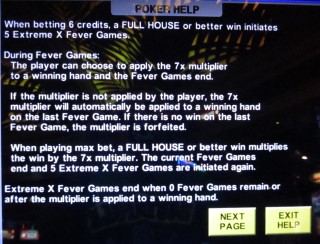
- If the player bets six coins and gets a full house or better on the draw, then he will earn five Fever Games.
- After the draw in every Fever Game, if there was a win less than a full house, then the player will have two options:
- Accept a multiplier (for example 6x or 7x) on the win and end the current set of Fever Games.
- Decline it to resume the remaining Fever Games, hoping for an even greater win.
- If the player gets a full house or better in a Fever Game, then the game will automatically apply the multiplier, end that current set of Fever Games, and start the player over with another five Fever Games, to begin the next game.
- The player must still make a six-coin bet during Fever Games.
Example
In the picture above, I got a full house on the draw, activating the Fever Games feature.
On the first Fever Game, I got a two pair on the draw and was faced with a tough choice — apply the 7x multiplier to the 10-coin win, to make it 70, or try for a higher win with my remaining four Fever Games. I chose to decline the multiplier and play on.
My second and third Fever Games were losers, so I was getting nervous about wasting the feature without getting another win to apply the multiplier to. Then a high pair came along on the fourth hand seen above. With only one hand left, I played it safe and accepted the multiplier, increasing a win of 5 to 35. This ended the feature.
Analysis
I'll use 9-5 Jacks or Better as the subject of my analysis. In this game, the Fever Games multiplier is 7x.
To analyze this game, I'll start at the end and work my way forward, as I usually do in games of multiple decision points. Due to the nature of betting six coins for a win based on five coins, I thought it would be easier to understand if I kept all the wins based on total coins won.
That said, the table below shows the return table for the 5th Fever Game. Wins for a full house and above are the sum of the multiplied win and a value of 76.56 coins for the value of the subsequent set of Fever Games. All Fever Game tables show the net win. In other words, the gross win less the six coins bet to play the game. The lower right cell shows a net expected win of the fifth Fever Game of 29.53 coins.
The astute reader may wonder how I knew the value of the Fever Game feature to do the analysis, when I would need to do the analysis itself to calculate it. In other words, it led to a circular logic error. The answer is I at first used an estimate and kept refining my analysis, step by step, until the estimated bonus value equaled the actual value.
Fever Game #5
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 28070.56 | 41,358,824 | 0.000025 | 0.698913 |
| Straight Flush | 1820.56 | 178,631,032 | 0.000108 | 0.195779 |
| Four of a Kind | 945.56 | 3,925,043,913 | 0.002363 | 2.234279 |
| Full House | 385.56 | 19,125,682,137 | 0.011514 | 4.439286 |
| Flush | 169.00 | 18,101,068,854 | 0.010897 | 1.841597 |
| Straight | 134.00 | 18,661,830,328 | 0.011235 | 1.505437 |
| Three of a Kind | 99.00 | 123,692,729,493 | 0.074464 | 7.371959 |
| Two Pair | 64.00 | 214,782,459,021 | 0.129301 | 8.275273 |
| Jacks Or Better | 29.00 | 357,280,539,372 | 0.215086 | 6.237505 |
| Nothing | -6.00 | 905,313,200,126 | 0.545007 | -3.270044 |
| Total | 1,661,102,543,100 | 1.000000 | 29.529983 |
The next table shows the return table for the fourth Fever Game. This is based on a strategy of accepting any win, since the extra 30 coins due to the multiplier are worth more than the expected 29.53 coins in the fifth Fever Game. The lower right cell shows that the expected value of the fourth Fever Game is 46.18 coins.
Fever Game #4
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 28070.56 | 1,077,328 | 0.000028 | 0.782836 |
| Straight Flush | 1820.56 | 4,845,031 | 0.000125 | 0.228336 |
| Four of a Kind | 945.56 | 89,474,142 | 0.002316 | 2.190075 |
| Full House | 385.56 | 434,042,298 | 0.011236 | 4.332082 |
| Flush | 169.00 | 633,110,761 | 0.016389 | 2.769736 |
| Straight | 134.00 | 613,780,761 | 0.015889 | 2.129071 |
| Three of a Kind | 99.00 | 2,760,961,551 | 0.071471 | 7.075670 |
| Two Pair | 64.00 | 4,767,292,881 | 0.123408 | 7.898122 |
| Jacks Or Better | 29.00 | 6,454,150,587 | 0.167075 | 4.845171 |
| Nothing | 23.53 | 22,871,556,360 | 0.592063 | 13.931226 |
| Total | 38,630,291,700 | 1.000000 | 46.182324 |
The next table shows the return table for the third Fever Game. This is based on a strategy of accepting a win of a two pair or greater. This is because the value of the fourth fever game of 46.18 is between the additional win of 30 and 60 for a high pair and two pair respectively. The lower right cell shows that the expected value of the third Fever Game is 58.75 coins.
Fever Game #3
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 28070.56 | 1,069,830 | 0.000028 | 0.777388 |
| Straight Flush | 1820.56 | 4,957,775 | 0.000128 | 0.233649 |
| Four of a Kind | 945.56 | 89,332,829 | 0.002313 | 2.186616 |
| Full House | 385.56 | 433,346,241 | 0.011218 | 4.325135 |
| Flush | 169.00 | 636,947,365 | 0.016488 | 2.786521 |
| Straight | 134.00 | 622,539,027 | 0.016115 | 2.159451 |
| Three of a Kind | 99.00 | 2,754,294,401 | 0.071299 | 7.058584 |
| Two Pair | 64.00 | 4,756,618,089 | 0.123132 | 7.880436 |
| Jacks Or Better | 45.18 | 6,407,187,438 | 0.165859 | 7.493902 |
| Nothing | 40.18 | 22,923,998,705 | 0.593420 | 23.845006 |
| Total | 38,630,291,700 | 1.000000 | 58.746688 |
The next table shows the return table for the second Fever Game. This is based on a strategy of accepting a win of a two pair or greater. This is because the value of the third fever game of 58.75 is between the additional win of 30 and 60 for a high pair and two pair respectively. The lower right cell shows that the expected value of the second Fever Game is 68.29 coins.
Fever Game #2
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 28070.56 | 1,069,458 | 0.000028 | 0.777118 |
| Straight Flush | 1820.56 | 5,201,830 | 0.000135 | 0.245151 |
| Four of a Kind | 945.56 | 88,644,741 | 0.002295 | 2.169773 |
| Full House | 385.56 | 430,779,849 | 0.011151 | 4.299520 |
| Flush | 169.00 | 640,259,267 | 0.016574 | 2.801010 |
| Straight | 134.00 | 654,362,888 | 0.016939 | 2.269841 |
| Three of a Kind | 99.00 | 2,726,326,584 | 0.070575 | 6.986909 |
| Two Pair | 64.00 | 4,718,128,446 | 0.122135 | 7.816669 |
| Jacks Or Better | 57.75 | 6,404,232,504 | 0.165783 | 9.573400 |
| Nothing | 52.75 | 22,961,286,133 | 0.594386 | 31.351868 |
| Total | 38,630,291,700 | 1.000000 | 68.291258 |
The next table shows the return table for the first Fever Game. This is based on a strategy of accepting a win of a three of a kind or greater. This is because the value of the second fever game of 68.29 is between the additional win of 60 and 90 for a two pair and three of a kind respectively. The lower right cell shows that the expected value of the first Fever Game is 76.56 coins.
Fever Game #1
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 28070.56 | 46,701,766 | 0.000028 | 0.789202 |
| Straight Flush | 1820.56 | 223,759,290 | 0.000135 | 0.245239 |
| Four of a Kind | 945.56 | 3,817,072,117 | 0.002298 | 2.172818 |
| Full House | 385.56 | 18,548,010,213 | 0.011166 | 4.305202 |
| Flush | 169.00 | 27,239,042,009 | 0.016398 | 2.771291 |
| Straight | 134.00 | 27,616,237,984 | 0.016625 | 2.227783 |
| Three of a Kind | 99.00 | 117,515,224,354 | 0.070745 | 7.003786 |
| Two Pair | 72.29 | 203,312,993,400 | 0.122396 | 8.848191 |
| Jacks Or Better | 67.29 | 279,983,746,599 | 0.168553 | 11.342141 |
| Nothing | 62.29 | 982,799,755,368 | 0.591655 | 36.854939 |
| Total | 1,661,102,543,100 | 1.000000 | 76.560590 |
Now that we know the value of the Fever Games feature is 76.56, we can analyze an initial spin. Unlike the other tables, this table shows the gross win, to be consistent with other pages on video poker. The return column is the product of the win, probability, and (1/6). The reason for dividing by six is that the player must bet six coins. So the table shows the relative return to a full bet. The lower right cell shows a return of 99.93%.
Extreme X Poker — Initial Spin
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 4076.56 | 41,307,611 | 0.000025 | 0.016896 |
| Straight Flush | 326.56 | 178,805,612 | 0.000108 | 0.005859 |
| Four of a Kind | 201.56 | 3,939,849,603 | 0.002372 | 0.079678 |
| Full House | 121.56 | 19,177,532,010 | 0.011545 | 0.233904 |
| Flush | 25.00 | 17,496,396,017 | 0.010533 | 0.043888 |
| Straight | 20.00 | 18,558,047,033 | 0.011172 | 0.037240 |
| Three of a Kind | 15.00 | 124,275,525,048 | 0.074815 | 0.187038 |
| Two Pair | 10.00 | 215,553,668,364 | 0.129765 | 0.216276 |
| Jacks Or Better | 5.00 | 355,927,380,069 | 0.214272 | 0.178560 |
| Nothing | 0.00 | 905,954,031,706 | 0.545393 | 0.000000 |
| Total | 1,661,102,543,073 | 1.000000 | 0.999337 |
It should be noted that IGT states the return for this game is 99.94%. This is 0.01% higher than what I get. If my return were just 0.0013% higher, I would round up to 99.94%. Although I tend to be a perfectionist when it comes to combinatorial-based analysis, I'll reluctantly accept a 0.0013% difference in this case, due to the complex recursive nature of the analysis.
Strategy
Speaking only for 9-5 Jacks or Better (a game nobody is ever likely to actually see in a casino) in a Fever Game the accept/reject strategy should be:
- On the first Fever Game, accept a three of a kind or better.
- On the second Fever Game, accept a two pair or better.
- On the third Fever Game, accept a two pair or better.
- On the fourth Fever Game, accept any win.
As far as when to hold 'em and when to throw 'em, it gets quite complicated. You can use my amazing video poker strategy maker but you have to be careful to put in the best value for each hand. Before you can do that, you have to go through a process of what I just went through above to get the average value of each state in the game. You can use my video poker analyzer to get the probability of each event, which is critical to getting the value of each stage of the game. The strategy maker doesn't allow a win for nothing, so you have to subtract the value of rejecting an offer, which is a win for nothing, from every other hand, to trick the calculator.
I wrote out a much longer explanation of how to do this, but it got very difficult to explain and would have been a major ordeal to do the math, so I erased it and left it as an exercise for the reader (I hate it when math books say that). However, to make up for it, I created direct links to the six strategies for 9-5 Jacks or Better Extreme X. Please be patient in waiting for the strategy maker to create the strategies.
Other Games and Pay Tables
IGT was kind enough for provide the games, pay tables, and returns available in Extreme X Poker. For their ongoing cooperation, the Wizard of Odds is always grateful. As usual, the returns assume optimal player strategy.
Bonus Poker
| Hand | 99.48% | 98.25% | 97.04% | 95.86% |
|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 |
| FOUR ACES | 80 | 80 | 80 | 80 |
| FOUR 2's, 3's, 4's | 40 | 40 | 40 | 40 |
| FOUR 5's THROUGH K's | 25 | 25 | 25 | 25 |
| FULL HOUSE | 7 | 6 | 6 | 6 |
| FLUSH | 5 | 5 | 5 | 4 |
| STRAIGHT | 4 | 4 | 3 | 3 |
| THREE OF A KIND | 3 | 3 | 3 | 3 |
| TWO PAIR | 2 | 2 | 2 | 2 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 |
Bonus Poker Deluxe
| Hand | 98.81% | 97.52% | 96.31% | 95.59% |
|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 |
| FOUR OF A KIND | 80 | 80 | 80 | 80 |
| FULL HOUSE | 8 | 8 | 7 | 6 |
| FLUSH | 6 | 5 | 5 | 5 |
| STRAIGHT | 4 | 4 | 4 | 4 |
| THREE OF A KIND | 3 | 3 | 3 | 3 |
| TWO PAIR | 1 | 1 | 1 | 1 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 |
Deuces Wild
| Hand | 99.88% | 98.96% | 97.83% | 97.60% | 96.06% | 95.00% |
|---|---|---|---|---|---|---|
| ROYAL FLUSH NO DEUCES | 800 | 800 | 800 | 800 | 800 | 800 |
| FOUR DEUCES | 200 | 200 | 200 | 200 | 200 | 200 |
| ROYAL FLUSH WITH DEUCE | 25 | 25 | 25 | 20 | 20 | 25 |
| FIVE OF A KIND | 16 | 15 | 16 | 12 | 10 | 15 |
| STRAIGHT FLUSH | 11 | 10 | 14 | 11 | 10 | 11 |
| FOUR OF A KIND | 4 | 4 | 4 | 4 | 4 | 4 |
| FULL HOUSE | 4 | 4 | 3 | 4 | 4 | 3 |
| FLUSH | 3 | 3 | 2 | 3 | 3 | 2 |
| STRAIGHT | 2 | 2 | 2 | 2 | 2 | 2 |
| THREE OF A KIND | 1 | 1 | 1 | 1 | 1 | 1 |
Deuces Wild Bonus Poker
| Hand | 99.53% | 99.52% | 97.41% | 96.64% | 95.42% |
|---|---|---|---|---|---|
| ROYAL FLUSH NO DEUCES | 800 | 800 | 800 | 800 | 800 |
| FOUR DEUCES + ONE ACE | 400 | 400 | 400 | 400 | 400 |
| FOUR DEUCES | 200 | 200 | 200 | 200 | 200 |
| ROYAL FLUSH WITH DEUCE | 25 | 25 | 25 | 25 | 25 |
| FIVE ACES | 80 | 80 | 80 | 80 | 80 |
| FIVE 3's, 4's, 5's | 40 | 40 | 40 | 40 | 40 |
| FIVE 6's THROUGH K's | 20 | 20 | 20 | 20 | 20 |
| STRAIGHT FLUSH | 13 | 9 | 10 | 12 | 10 |
| FOUR OF A KIND | 4 | 4 | 4 | 4 | 4 |
| FULL HOUSE | 3 | 4 | 3 | 3 | 3 |
| FLUSH | 3 | 3 | 3 | 2 | 2 |
| STRAIGHT | 1 | 1 | 1 | 1 | 1 |
| THREE OF A KIND | 1 | 1 | 1 | 1 | 1 |
Double Bonus Poker
| Hand | 99.35% | 98.01% | 96.54% | 94.28% |
|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 |
| FOUR ACES | 160 | 160 | 160 | 160 |
| FOUR 2's, 3's, 4's | 80 | 80 | 80 | 80 |
| FOUR 5's THROUGH K's | 50 | 50 | 50 | 50 |
| FULL HOUSE | 9 | 9 | 9 | 8 |
| FLUSH | 7 | 6 | 6 | 5 |
| STRAIGHT | 5 | 5 | 4 | 4 |
| THREE OF A KIND | 3 | 3 | 3 | 3 |
| TWO PAIR | 1 | 1 | 1 | 1 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 |
Double Double Bonus Poker
| Hand | 99.48% | 98.25% | 97.04% | 95.86% | |
|---|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 | 50 |
| FOUR A's + ANY 2, 3 OR 4 | 400 | 400 | 400 | 400 | 400 |
| FOUR 2's,3's,4's + ANY A,2,3,4 | 160 | 160 | 160 | 160 | 160 |
| FOUR ACES | 160 | 160 | 160 | 160 | 160 |
| FOUR 2's, 3's, 4's | 80 | 80 | 80 | 80 | 80 |
| FOUR 5's THROUGH K's | 50 | 50 | 50 | 50 | 50 |
| FULL HOUSE | 9 | 9 | 8 | 7 | 6 |
| FLUSH | 6 | 5 | 5 | 5 | 5 |
| STRAIGHT | 4 | 4 | 4 | 4 | 4 |
| THREE OF A KIND | 3 | 3 | 3 | 3 | 3 |
| TWO PAIR | 1 | 1 | 1 | 1 | 1 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 | 1 |
Jacks or Better
| Hand | 99.94% | 98.71% | 97.49% | 96.26% |
|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 |
| FOUR OF A KIND | 25 | 25 | 25 | 25 |
| FULL HOUSE | 9 | 8 | 7 | 6 |
| FLUSH | 5 | 5 | 5 | 5 |
| STRAIGHT | 4 | 4 | 4 | 4 |
| THREE OF A KIND | 3 | 3 | 3 | 3 |
| TWO PAIR | 2 | 2 | 2 | 2 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 |
Triple Double Bonus Poker
| Hand | 99.73% | 98.25% | 97.19% | 95.98% | 95.02% |
|---|---|---|---|---|---|
| ROYAL FLUSH | 800 | 800 | 800 | 800 | 800 |
| STRAIGHT FLUSH | 50 | 50 | 50 | 50 | 50 |
| FOUR A's + ANY 2, 3 OR 4 | 800 | 800 | 800 | 800 | 800 |
| FOUR 2's,3's,4's + ANY A,2,3,4 | 400 | 400 | 400 | 400 | 400 |
| FOUR ACES | 160 | 160 | 160 | 160 | 160 |
| FOUR 2's, 3's, 4's | 80 | 80 | 80 | 80 | 80 |
| FOUR 5's THROUGH K's | 50 | 50 | 50 | 50 | 50 |
| FULL HOUSE | 9 | 9 | 9 | 8 | 7 |
| FLUSH | 7 | 6 | 5 | 5 | 5 |
| STRAIGHT | 4 | 4 | 4 | 4 | 4 |
| THREE OF A KIND | 2 | 2 | 2 | 2 | 2 |
| TWO PAIR | 1 | 1 | 1 | 1 | 1 |
| JACKS OR BETTER | 1 | 1 | 1 | 1 | 1 |