On this page
Hot Numbers in Roulette -- Myths and Facts
Introduction
The Gambler's Fallacy is the mistaken belief that if an independent event has not happened in a long time, then it becomes overdue and more likely. It is also equally incorrect that if an outcome has happened a disproportionate number of times lately, compared to statistical expectations, then it becomes overheated and less likely to occur the next time. An example of this fallacious thinking might be that if the number 23 hasn't been drawn in a 6-49 lottery the last 100 games, then it becomes more likely to be drawn during the next drawing.
Many worthless betting strategies and systems are based on belief in the Gambler's Fallacy. I got the idea for writing about this after reading an 888 online roulette article by Frank Scoblete entitled How to Take Advantage of Roulette Hot Spots. In that article, Scoblete recommends taking a count of each outcome for 3,700 spins in single-zero roulette and 3,800 spins in double-zero roulette in the hunt for "hot numbers." Never mind that this would take about 100 hours to make this many observations, assuming the industry standard of 38 spins per hour.
Before going further, let me say that I strongly believe modern roulette wheels made by top brands like Cammegh are extremely precise and any bias would be minuscule compared to the house advantage. Thus, testing a modern roulette for bias would be a total waste of time. Now, testing a 30-year-old hand-me-down wheel in a banana republic might be another story. However, you're on your own if you win a lot of money from said casino and try to leave with it.
That said, if you track 3,800 outcomes in single-zero roulette, the average number of times any number will hit is 3800/38=100. I ran a simulation of over 1.3 trillion spins, counting how many times each number was hit, sorting the outcomes to find the most frequent number and how many times it was observed, and keeping a count of how many times the most frequent number in each simulation was seen.
Hottest Number in 3,800 Spins of Double-Zero Roulette
As a former actuary, I hate to use a layman's term like the "hottest number," but that is how gamblers talk so will go with that. That said, following are the results of the count of the hottest number in millions of 3800-spin simulations.
Count of the Hottest Number in 3,800 Spins on Double-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 122.02 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
Here is what the table above means in plain simple English.
- The mean, or average, count of the hottest number is 122.02.
- The median count of the most frequent number is 121. This means that over 50% of time the most frequent number appeared 121 times or less, as well as 121 times or more. This is possible because the probability of 121 observations is in both groups.
- The mode, or most count of the hottest number is 120, which happens 8.29% of the time.
- The 90th percentile is the smallest number such that the probability the count of the hottest number is at least 90% .
- The 95th percentile is the smallest number such that the probability the count of the hottest number is at least 95%.
- The 99th percentile is the smallest number such that the probability the count of the hottest number is at least 99%.
- The 99.9th percentile is the smallest number such that the probability the count of the hottest number is at least 99.9%.
Hottest Number in 3,700 Spins of Single-Zero Roulette
The results are very similar with 3,700 spins tracked on a single-zero wheel. Following is a summary of the results.
Count of the Hottest Number in 3,700 Spins on Single-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 121.90 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
The following table shows the full results of the simulation on both wheels. The two commulative columns show the probability that the count of the hottest number is the number on the left column or more. For example, the probability the hottest number in 3,700 spins of single-zero roulette is 130 or more is 0.072044.
Summary of the Count of the Hottest Number in 3,700 Spins of Single-Zero Roulette and 3,800 spins of Double-Zero Roulette
| Count | Probability Single Zero |
Cummulative Single Zero |
Probability Double Zero |
Cummulative Double Zero |
|---|---|---|---|---|
| 160 or More | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 159 | 0.000000 | 0.000001 | 0.000000 | 0.000001 |
| 158 | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 157 | 0.000001 | 0.000002 | 0.000001 | 0.000002 |
| 156 | 0.000001 | 0.000003 | 0.000001 | 0.000003 |
| 155 | 0.000002 | 0.000005 | 0.000002 | 0.000005 |
| 154 | 0.000003 | 0.000009 | 0.000003 | 0.000008 |
| 153 | 0.000005 | 0.000013 | 0.000005 | 0.000013 |
| 152 | 0.000007 | 0.000020 | 0.000008 | 0.000021 |
| 151 | 0.000012 | 0.000032 | 0.000012 | 0.000033 |
| 150 | 0.000017 | 0.000049 | 0.000018 | 0.000051 |
| 149 | 0.000026 | 0.000075 | 0.000027 | 0.000077 |
| 148 | 0.000038 | 0.000114 | 0.000041 | 0.000118 |
| 147 | 0.000060 | 0.000174 | 0.000062 | 0.000180 |
| 146 | 0.000091 | 0.000265 | 0.000092 | 0.000273 |
| 145 | 0.000132 | 0.000397 | 0.000137 | 0.000409 |
| 144 | 0.000195 | 0.000592 | 0.000199 | 0.000608 |
| 143 | 0.000282 | 0.000874 | 0.000289 | 0.000898 |
| 142 | 0.000409 | 0.001283 | 0.000421 | 0.001319 |
| 141 | 0.000580 | 0.001863 | 0.000606 | 0.001925 |
| 140 | 0.000833 | 0.002696 | 0.000860 | 0.002784 |
| 139 | 0.001186 | 0.003882 | 0.001215 | 0.003999 |
| 138 | 0.001652 | 0.005534 | 0.001704 | 0.005703 |
| 137 | 0.002315 | 0.007849 | 0.002374 | 0.008077 |
| 136 | 0.003175 | 0.011023 | 0.003286 | 0.011363 |
| 135 | 0.004355 | 0.015378 | 0.004489 | 0.015852 |
| 134 | 0.005916 | 0.021295 | 0.006088 | 0.021940 |
| 133 | 0.007939 | 0.029233 | 0.008196 | 0.030136 |
| 132 | 0.010601 | 0.039834 | 0.010908 | 0.041044 |
| 131 | 0.013991 | 0.053824 | 0.014384 | 0.055428 |
| 130 | 0.018220 | 0.072044 | 0.018757 | 0.074185 |
| 129 | 0.023498 | 0.095542 | 0.024114 | 0.098299 |
| 128 | 0.029866 | 0.125408 | 0.030603 | 0.128901 |
| 127 | 0.037288 | 0.162696 | 0.038228 | 0.167130 |
| 126 | 0.045771 | 0.208467 | 0.046898 | 0.214027 |
| 125 | 0.055165 | 0.263632 | 0.056310 | 0.270337 |
| 124 | 0.064853 | 0.328485 | 0.066020 | 0.336357 |
| 123 | 0.074178 | 0.402662 | 0.075236 | 0.411593 |
| 122 | 0.081929 | 0.484591 | 0.082885 | 0.494479 |
| 121 | 0.087158 | 0.571750 | 0.087696 | 0.582174 |
| 120 | 0.088520 | 0.660269 | 0.088559 | 0.670734 |
| 119 | 0.084982 | 0.745252 | 0.084406 | 0.755140 |
| 118 | 0.076454 | 0.821705 | 0.075245 | 0.830385 |
| 117 | 0.063606 | 0.885312 | 0.061851 | 0.892236 |
| 116 | 0.048069 | 0.933381 | 0.046111 | 0.938347 |
| 115 | 0.032432 | 0.965813 | 0.030604 | 0.968952 |
| 114 | 0.019117 | 0.984930 | 0.017664 | 0.986616 |
| 113 | 0.009567 | 0.994496 | 0.008614 | 0.995230 |
| 112 | 0.003894 | 0.998390 | 0.003420 | 0.998650 |
| 111 | 0.001257 | 0.999647 | 0.001065 | 0.999715 |
| 110 | 0.000297 | 0.999944 | 0.000243 | 0.999958 |
| 109 | 0.000050 | 0.999994 | 0.000038 | 0.999996 |
| 108 or Less | 0.000006 | 1.000000 | 0.000004 | 1.000000 |
Count of the Hottest Numbers in 300 Spins in Double-Zero Roulette
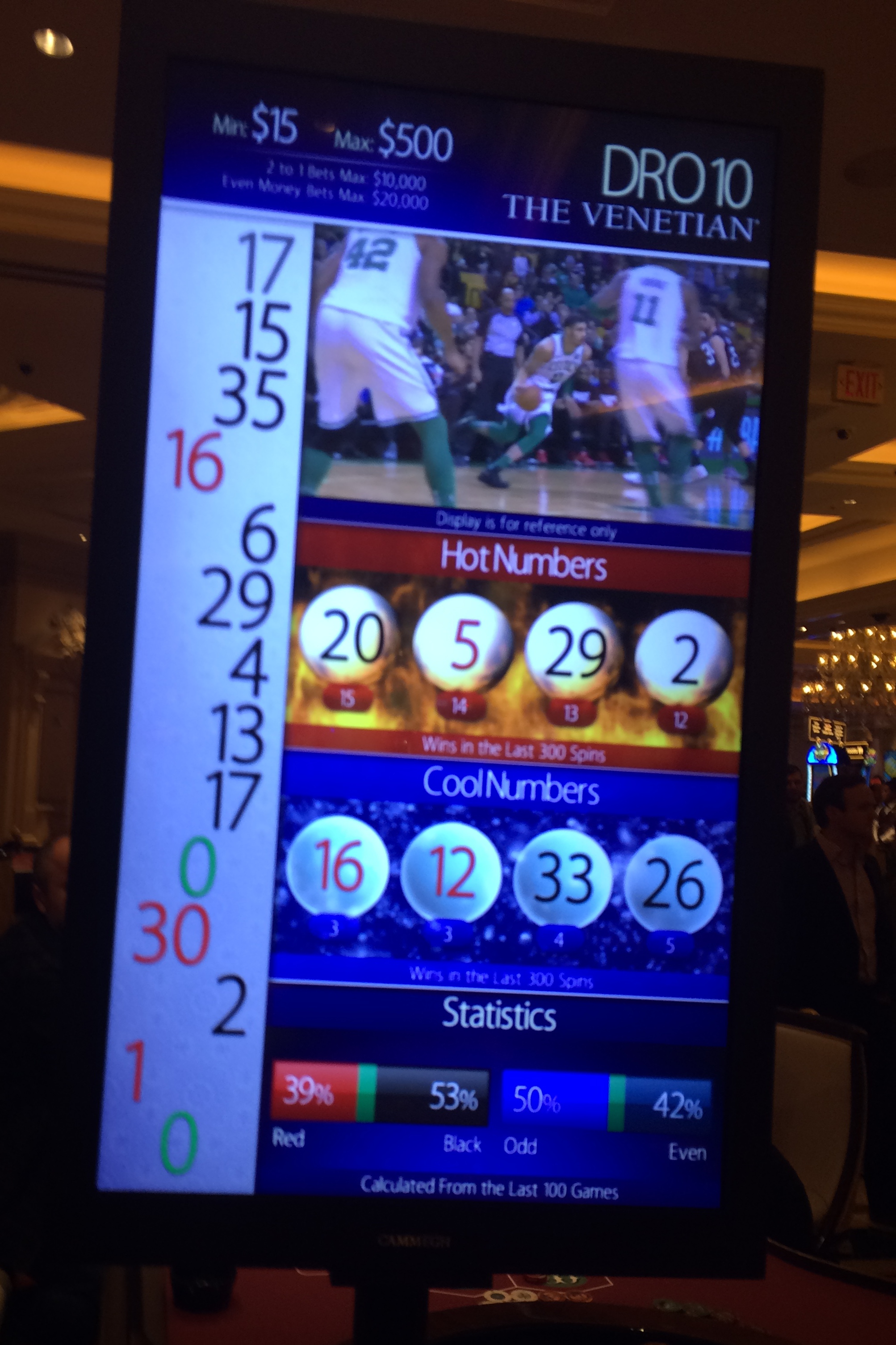
What if you don't want to spend 100 hours gathering data on a single wheel? Some casinos are kind enough to give you, on a silver platter, the number of times in the last 300 spins the four "hottest" and "coolest" numbers occurred. The image at the top of the page shows an example taken on a double-zero wheel at the Venetian.
In 300 spins, the average number of wins on a double-zero wheel for any number is 300/38=7.9. As you can see from the image above, the four hottest numbers were 20, 5, 29, and 2, which occurred 15, 14, 13, and 12 times respectively. Is this unusual? No. In a simulation of over 80 billion spins, the most frequent number, in 300-spin experiments, appeared most frequently at 14 times with a probability of 27.4%. The most likely total of the second, third, and fourth most frequent numbers was 13, 12, and 12 times respectively, with probabilities of 37.9%, 46.5%, and 45.8%. So the results of the "hottest" numbers in the image above were a little more flat than average.
The following table shows the probabilities of the four hottest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.009210.
Count of the Hottest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Most Frequent |
Probability Second Most Frequent |
Probability Third Most Frequent |
Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000022 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000051 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000166 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000509 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.001494 | 0.000001 | 0.000000 | 0.000000 |
| 20 | 0.004120 | 0.000009 | 0.000000 | 0.000000 |
| 19 | 0.010806 | 0.000075 | 0.000000 | 0.000000 |
| 18 | 0.026599 | 0.000532 | 0.000003 | 0.000000 |
| 17 | 0.060526 | 0.003263 | 0.000060 | 0.000001 |
| 16 | 0.123564 | 0.016988 | 0.000852 | 0.000020 |
| 15 | 0.212699 | 0.071262 | 0.009210 | 0.000598 |
| 14 | 0.274118 | 0.215025 | 0.068242 | 0.011476 |
| 13 | 0.212781 | 0.379097 | 0.283768 | 0.117786 |
| 12 | 0.067913 | 0.270747 | 0.464748 | 0.457655 |
| 11 | 0.004615 | 0.042552 | 0.168285 | 0.383900 |
| 10 | 0.000017 | 0.000448 | 0.004830 | 0.028544 |
| 9 | 0.000000 | 0.000000 | 0.000001 | 0.000020 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary of the Count of the Four Most Frequent Numbers in 300 Spins of Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.48 | 14 | 14 |
| Second | 13.07 | 13 | 13 |
| Third | 12.27 | 12 | 12 |
| Fourth | 11.70 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Double-Zero Roulette
The next table shows the probability of each count of the four collest numbers in 300 spins of double-zero roulette.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent |
Probability Second Least Frequent |
Probability Third Least Frequent |
Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.012679 | 0.000063 | 0.000000 | 0.000000 |
| 1 | 0.098030 | 0.005175 | 0.000135 | 0.000002 |
| 2 | 0.315884 | 0.088509 | 0.012041 | 0.001006 |
| 3 | 0.416254 | 0.420491 | 0.205303 | 0.063065 |
| 4 | 0.150220 | 0.432638 | 0.595139 | 0.522489 |
| 5 | 0.006924 | 0.052945 | 0.185505 | 0.401903 |
| 6 | 0.000008 | 0.000180 | 0.001878 | 0.011534 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of double-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.61 | 3 | 3 |
| Second Least | 3.44 | 3 | 4 |
| Third Least | 3.96 | 4 | 4 |
| Fourth Least | 4.36 | 4 | 4 |
Count of the Hottest Numbers in 300 Spins of Single-Zero Roulette
In 300 spins, the average number of wins on a single-zero wheel for any number is 300/37=8.11. The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.015727.
Count of the Hottest Four Numbers in 300 Spins on a Single-Zero Wheel
| Observations | Probability Most Frequent |
Probability Second Most Frequent |
Probability Third Most Frequent |
Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000034 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000078 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000245 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000728 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.002069 | 0.000002 | 0.000000 | 0.000000 |
| 20 | 0.005570 | 0.000018 | 0.000000 | 0.000000 |
| 19 | 0.014191 | 0.000135 | 0.000000 | 0.000000 |
| 18 | 0.033833 | 0.000905 | 0.000008 | 0.000000 |
| 17 | 0.074235 | 0.005202 | 0.000125 | 0.000001 |
| 16 | 0.144490 | 0.025286 | 0.001624 | 0.000050 |
| 15 | 0.232429 | 0.097046 | 0.015727 | 0.001286 |
| 14 | 0.269735 | 0.259360 | 0.101259 | 0.021054 |
| 13 | 0.177216 | 0.382432 | 0.347102 | 0.175177 |
| 12 | 0.043266 | 0.208137 | 0.429715 | 0.508292 |
| 11 | 0.001879 | 0.021373 | 0.102979 | 0.283088 |
| 10 | 0.000003 | 0.000103 | 0.001461 | 0.011049 |
| 9 | 0.000000 | 0.000000 | 0.000000 | 0.000002 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary — Count of the Four Hottest Numbers — Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.74 | 15 | 14 |
| Second | 13.30 | 13 | 13 |
| Third | 12.50 | 12 | 12 |
| Fourth | 11.92 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Single-Zero Roulette
The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third coolest numbers will be observed five times is 0.287435.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent |
Probability Second Least Frequent |
Probability Third Least Frequent |
Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.009926 | 0.000038 | 0.000000 | 0.000000 |
| 1 | 0.079654 | 0.003324 | 0.000068 | 0.000001 |
| 2 | 0.275226 | 0.062392 | 0.006791 | 0.000448 |
| 3 | 0.419384 | 0.350408 | 0.140173 | 0.034850 |
| 4 | 0.200196 | 0.484357 | 0.557907 | 0.406702 |
| 5 | 0.015563 | 0.098547 | 0.287435 | 0.521238 |
| 6 | 0.000050 | 0.000933 | 0.007626 | 0.036748 |
| 7 | 0.000000 | 0.000000 | 0.000001 | 0.000013 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of single-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Single-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.77 | 3 | 3 |
| Second Least | 3.62 | 4 | 4 |
| Third Least | 4.15 | 4 | 4 |
| Fourth Least | 4.56 | 5 | 5 |
The least I hope you have learned from this article is it is to be expected that certain numbers will come up more than others. To put it in other words, it is natural that some numbers will be "hot" and some "cool." In fact, such differences from the mean are highly predictable. Unfortunately, for roulette players, we don't know which numbers will be "hot," just that some of them almost certainly will be. I would also like to emphasize, contrary to the Gambler's Fallacy, that on a fair roulette wheel that every number is equally likely every spin and it makes no difference what has happened in the past.
Finally, it should not be interpreted that we give an endorsement to the 888 Casino, which we linked to earlier. I am very bothered by this rule in their rule 6.2.B. Before getting to that, let me preface with a quote from rule 6.1, which I'm fine with.
"If we reasonably determine that you are engaging in or have engaged in fraudulent or unlawful activity or conducted any prohibited transaction (including money laundering) under the laws of any jurisdiction that applies to you (examples of which are set out at section 6.2 below), any such act will be considered as a material breach of this User Agreement by you. In such case we may close your account and terminate the User Agreement in accordance with section 14 below and we are under no obligation to refund to you any deposits, winnings or funds in your account." -- Rule 6.1
Let's go further now:
The following are some examples of "fraudulent or unlawful activity" -- Rule 6.2
Next, here is one of many examples listed as rule 6.2.B
"Unfair Betting Techniques: Utilising any recognised betting techniques to circumvent the standard house edge in our games, which includes but is not limited to martingale betting strategies, card counting as well as low risk betting in roulette such as betting on red/black in equal amounts." -- Rule 6.2.B
Let me make it perfectly clear that all betting systems, including the Martingale, not only can't circumvent the house edge, they can't even dent it. It is very mathematically ignorant on the part of the casino to fear any betting system. Why would any player trust this casino when the casino can seize all their money under the reason that the player was using a betting system? Any form of betting could be called a betting system, including flat betting. Casino 888 normally has a pretty good reputation, so I'm surprised they would lower themselves to this kind of rogue rule.