Probability - General Questions
Are you saying that in the long run you will lose at every casino game no matter what you do?
With the exception of rare positive expectation opportunities in blackjack and video poker, yes, that is what I'm saying.
How can I convert your probabilities into the x to y format?
Saying the odds of something happening are x to y means that the event in question will happen x times for every y times it doesn't happen. To make the conversion let p be the probability of some event. The odds could also be expressed as (1/p)-1 to 1. Lets look at an example. The probability of drawing a full house in five-card stud is 0.00144058. This could also be represented as 693.165 to 1.
I was recently looking at a football pool that was taking place. This was one of those where there is a grid of 100 boxes and the numbers 0-9 run along the X and Y axises and correspond to the last number of the score. I am not a football fan and did not bet on this pool but I am a gambler and don't think it is such a great bet.
I am taking for granted that you know the type of pool that I am referring to. Each box costs $5 and pay outs are each quarter. If your box wins you win $125 and it is possible to win all 4 quarters if the last numbers remain the same winning $500 for a payout of 100 to 1.
The person soliciting the bet was trying to tell me that the odds of winning the $500 are 100 to 1. I disagree. First the box that has 0 + 7 stands a much better chance of winning than the 2 + 9 box. However, the odds of 0 + 7 remaining the last 2 numbers throughout the game must be high. If the boxes are chosen for you through a random process, can you tell me the approximate odds of winning the $500 prize?
Assuming the cells in the grid are chosen at random, then the odds of winning any one quarter would be 1/100. Assuming each quarter was an independent event, which they aren't, the odds of winning all four quarters would be (1/100)4 = 1 in 100 million.
I'd really like to know how to read odds like 12 to 1, or 3 to 2. Which one shows the best chances of winning? 12 to 1 or 3 to 2?
I don't like using probabilities in that form but they are generally used in this kind of syntax, "The odds against drawing a royal flush are 649,739 to 1." That means there are 649,739 ways you can't draw a royal flush and 1 way you can. In your examples 12 to 1 is a probability of 1/13, or 7.69%, and 3 to 2 is 2/5, or 40.00%, so the 3 to 2 is the better chance of winning.
In a St. Louis Post-Dispatch article, the reporter says, "A 500-year flood is one that has a 1-in-500 chance of happening in any given year. Stated another way, that would be a 1-in-10 chance of happening over 50 years, or a 1-in-5 chance of happening over a century." After reading through all your gambling pages, I believe this is not a correct way to put it, right? Extrapolating their assertion, it would mean that there is a 1-in-1 chance that a flood will occur every 500 years, and that can't possibly be right.
You are right, that article is incorrect. The probability of a 500-year flood in a period of x years is 1-e-x/500. So the probability of at least one 500-year flood in 50 years is 9.52% and in 100 years is 18.13%.
If I determine the fair line of a game to be -160/+160 and I find a rogue line of -145 what is my EV? Any formula you could provide in which I could derive my EV +/- after a fair line has been determined would be greatly appreciated.
Let p be the probability of the favorite winning. If -160 is a fair line then:
100*p - 160*(1-p) = 0
260p = 160
p = 160/260 = 8/13 = 61.54%.
So the expected return on a $145 bet at a -145 line would be (8/13)*100 + (5/13)*-145 = 75/13 = $5.77. So the player advantage would be $5.77/$145 = 3.98%.
Let’s define t as the true money line with no house edge and a as the actual money line. Following are the formulas for the player’s expected return:
A is negative, t is negative: (100*(t-a) / (a*(100-t))
A is positive, t is positive: (a-t)/(100+t)
A is positive, t is negative: (a*t + 10000)/((t-100)*100)
So in your case your expected return is 100*(-160 -(-145))/(-145*(100-(-160))) = 3.98%.
What do you think of the claim below, that God is a Democrat as evidenced by the fact that all the counties that voted for Gore in 2000 were spared by the three hurricanes that hit Florida recently?
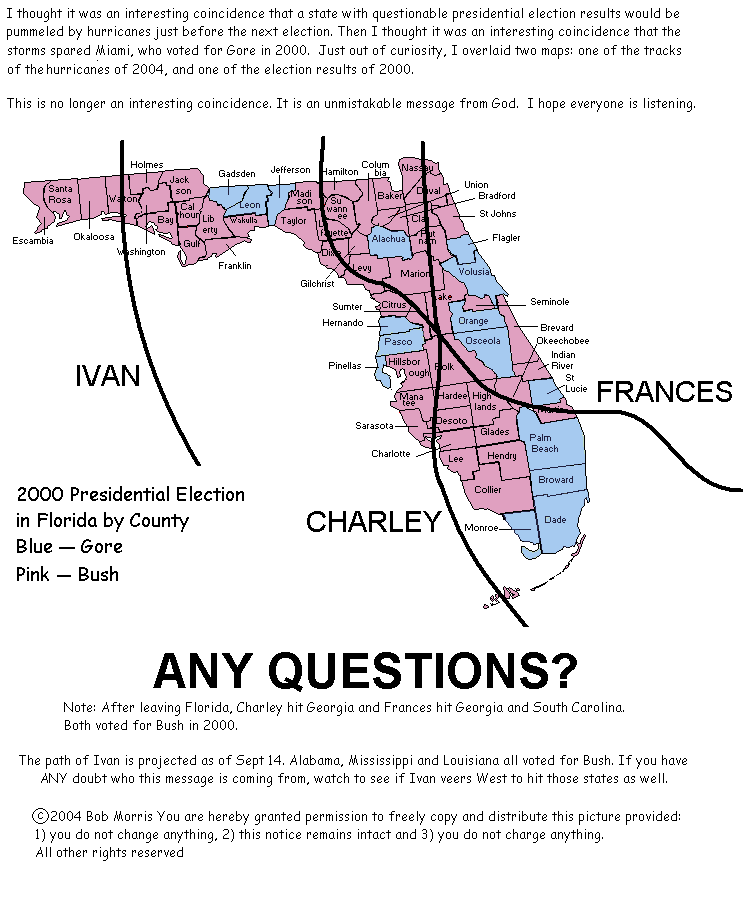
First, I am publishing this because author gives permission to do so at the bottom. This is a good example that correlation does not necessarily mean causation. It is easy to look back in time and find lots of coincidences. To make a case for anything a hypothesis should be stated before any evidence is gathered.
Follow-up (November 13, 2004): Another reader pointed out that this map started out as a joke but turned into an urban legend. As this link points out the hurricane paths in the graphic were simply not accurate and the actual hurricanes hit many Gore counties. It just goes to show you shouldn’t believe everything you read, especially on the Internet.
Just thought you might find this interesting. At Bodog they offer the following bet, “Will Britney Spears and Kevin Federline's second baby be a Boy or Girl?” The odds on a boy are +105, and for a girl −145. Last I checked this has been 1:1 since the beginning of mankind. I'd like to know who is taking the -145 side of this one. Love the site, visit often, and click your sponsors in appreciation.
Thanks for the kind words. To be honest nobody cares much about click-through rates any longer. So don't feel obligated to click through the banners if it is just for show. To answer your question, in the United States the probabilities are very close to 50.5% boy and 49.5% girl. Assuming no other information is known by the betting community the player advantage on the boy bet would be .505*1.05 - .495 = 3.53%. It could be that somebody with inside knowledge is betting on a girl. Another theory is that some people incorrectly believe you can tell the gender by the shape of the mother’s belly, and these people are betting on a girl. Personally I’m going to leave this one alone.
In this YouTube video, Matt Damon says John McCain has a 1 in 3 chance of not surviving his first term. Is he right?
No. Using this actuarial table from the CDC (Centers for Disease Control), the probability of a 72 year old white male making it to age 76 is 85.63%. That is about a 1 in 7 chance of death. The survival rate can be found by dividing the birth cohort at age 76 of 57,985, by birth cohort at age 72 of 67,719, from the white male table on page 14. The table used is a called a "period life table," which assumes 2003 rates of mortality will not change in the future, and is the most commonly used kind of actuarial table. A perfectionist might want to use a 1936 cohort life table, but I don’t think it would make much difference.
p.s. After posting this answer I have received several comments that my response did not take into consideration John McCain’s individual health situation. Working against him is being a cancer survivor. Working in his favor is access to the best medical care money can buy, he is obviously still in good shape mentally and physically for a 72-year old, and longevity, as evidenced by the fact that his mother is still alive. However, I never intended to factor in this information. It was Matt Damon who quoted actuarial tables, which is what I was referring to. All I am saying is that for the average 72-year old white male, the probability of surviving four more years is 86%. If forced, I would predict John McCain’s odds are even better than that.
Given an equal amount of paper, which paper cup would hold more water, a cylinder or cone shape? Assume the cylinder is open on one end and optimal dimensions in both cases.
Please see my companion site MathProblems.info, problem number 210, for the answer and solution.
Have you heard the story of Princess, the camel at the Popcorn Park zoo in New Jersey, who has an 88-51 record against the spread in handicapping the NFL? What are the odds of that?
Not counting pushes, the probability of getting at least 88 wins out of 139 picks is 0.00107355, or 1 in 931. This is pretty underwhelming. I'm sure there are 930 other animals out there who did worse that nobody writes about. For more information on Princess, read the article N.J. camel predicts Giants over Patriots at ESPN.com.
On the May 8, 2012 Chelsea Lately show, Chelsea said that red heads are dying out because they don't mate with each other. Is this true?
I hope you're happy; I spent hours on this.
To answer the question it is important to quantify behavior under the Chelsea Handler red head hypothesis. Here are my assumptions.
- A red head will never mate with another red head.
- The female will always choose the male to mate with.
- Everybody will mate and each mating will produce the same number of children.
- The female redheads will get first dibs at a mate, choosing randomly among the non-red heads.
- The female carriers (with one red-haired gene) will choose a mate randomly among the men left over by the red heads.
- The negative females (neither red-haired gene) will chose randomly among the men left over by the red heads and the carriers.
I start with a red-haired probability of 4%, according to Today I Found It. I then assume that prior to now there was no bias against red heads.
Assuming the bias against red heads starts with the next generation, and continues, what will be the trend of the total population to have red hair? After a lot of work in a spreadsheet, which I won't get into, here are the first eight generations, starting from this one.
Red Hair Proportion
| Generation | Proportion |
|---|---|
| 1 | 4.000000% |
| 2 | 3.888889% |
| 3 | 3.895219% |
| 4 | 3.894863% |
| 5 | 3.894883% |
| 6 | 3.894882% |
| 7 | 3.894882% |
| 8 | 3.894882% |
What we see is that by the third generation the proportion of the population with red hair will converge to 3.90%. So, despite what Chelsea may say, I think the red heads have nothing to worry about.
This question was raised and discussed in my forum at Wizard of Vegas.
According to CardPlayer.com, Amir Lehavot, who is one of the nine players to make the 2013 final table in the World Series of Poker, is selling any winnings above the minimum $733,224 for ninth place at a price of $29,248 for each 1% share. Is that a fair price?
First, let's review the chip stacks.
2013 WSOP Final Table Chip Stacks
| Player | Chips |
|---|---|
| JC Tran | 38,000,000 |
| Amir Lehavot | 29,700,000 |
| Marc McLaughlin | 26,525,000 |
| Jay Farber | 25,975,000 |
| Ryan Riess | 25,875,000 |
| Sylvain Loosli | 19,600,000 |
| Michiel Brummelhuis | 11,275,000 |
| Mark Newhouse | 7,350,000 |
| David Benefield | 6,375,000 |
The next table shows the win for each final outcome in the tournament.
2013 WSOP Final Table Prize Money
| Place | Win |
|---|---|
| 1st | $8,359,531 |
| 2nd | $5,173,170 |
| 3rd | $3,727,023 |
| 4th | $2,791,983 |
| 5th | $2,106,526 |
| 6th | $1,600,792 |
| 7th | $1,225,224 |
| 8th | $944,593 |
| 9th | $733,224 |
Assuming each player is of equal skill, the probability of winning could be estimated as the share of the total chip stack. However, it gets more complicated for every position after that. To help answer the question, I developed my poker tournament calculator.
After putting in the information above, you'll see that Amir has an expected win of $ 3,658,046. Then subtract out the minimum prize of $733,224 for 9th place and you get $2,924,822 in expected non-guaranteed winnings. Each 1% share has a value of $29,248.22. This is conveniently the price quoted in the cardplayer.com article.
By the way, Lehavot finished third, for $3,727,023 in prize money. Subtracting the $733,224 guaranteed money for 9th place and dividing by 100, each 1% share returned $29,938. The original cost per share was $29,248, so each share would have seen a 2.36% profit.
This question is discussed in my forum at Wizard of Vegas.
For casino promotions that still use regular tickets in a real drum (not the electronic ones) where you print your tickets at the players desk and put them into the drum -- do you bend / crease your tickets before you put them into the drum? Do you think that the bent ones have a better chance of being picked?
I hope you're happy. To answer this question, I bought a big roll of tickets at the Office Depot. Then I put 500 of them in a paper bag, half folded in half, at about a 90-degree angle, and the other half unfolded. Then I had six volunteers each draw 40 to 60 of them one at a time, with replacement, as I recorded the results. Here are the results.
Drawing Ticket Experiment
| Subject | Folded | Unfolded | Total |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| Total | 175 | 125 | 300 |
So, 58.3% of the tickets drawn were folded!
If it's assumed that folding had no effect, then these results would be 2.89 standard deviations away from expectations. The probability of getting this many folded tickets, or more, assuming folding didn't affect the odds, is 0.19%, or 1 in 514.
I might add the subjects who drew tickets hastily were much more likely to draw folded ones. Those who carefully took their time with each draw were at or near a 50/50 split.
So, my conclusion is definitely to fold them.
For discussion about this question, please visit my forum at Wizard of Vegas.
Two players each are dealt a random number in (0,1). First player decides to either stand pat or discard and draw a new number. Second player then does the same. High number wins. What is the optimal strategy for each player? Assuming optimal strategy, what is the probability each player wins?
Suppose you were offered the opportunity to play a coin flipping game. If the first flip is heads, then you get back $2 and the game is over. Otherwise, you flip again. If the second flip is heads, then you get back $4. If the second flip is also tails, you keep flipping until you do get heads. For each flip, the prize doubles. In other words, you get back 2^n, where n is the number of flips (including the ending flip on heads). How much would you pay to play this game? I hear the mathematical answer is an infinite amount of money, but this doesn't make sense, because you must win a finite amount of money at some point.
This is known as the Saint Petersburg Paradox.
It is indeed true that the expected win of the game is ∞, while at the same time the probability is that the coin will eventually land on tails, leading to a finite amount of money. The calculation of the expected win is:
Expected win = pr(1 flip)×2 +
pr(2 flips)×4 +
pr(3 flips)×8 +
pr(4 flips)×16 +
pr(5 flips)×32 +
pr(6 flips)×64 + ... =
(1/2)1 × 21 +
(1/2)2 × 22 +
(1/2)3 × 23 +
(1/2)4 × 24 +
(1/2)5 × 25 +
(1/2)6 × 26 + ...
= ((1/2)*(2/1)) 1 +
((1/2)*(2/1)) 2 +
((1/2)*(2/1)) 3 +
((1/2)*(2/1)) 4 +
((1/2)*(2/1)) 5 +
((1/2)*(2/1)) 6 + ...
= 11 + 12 +
13 +
14 +
15 +
16 + ...
= 1 + 1 + 1 + 1 + 1 + 1 + ...
= ∞
Where this is paradoxical is the player must win a finite amount of money, but the expected win is infinite. How can that be?
This is probably not a very satisfying answer, but there are lots of paradoxes when it comes to ∞. This may cause me to get some angry emails, but what lets me sleep at night, despite such infinity paradoxes, is that I believe that ∞ is a mathematical or philosophical concept that is unproven to exist in the real physical universe. This concept or theory of infinity carries with it built-in paradoxes.
For those who disagree with this, please tell me anything that is proven to have infinite quantity or measurement. Please don't say a black hole has infinite density unless you have evidence of its size.
To answer the initial question of how much should one pay to play this game, we should keep in mind that happiness is not proportional to the amount of money. Personally, I was taught in economics classes, and believe, that the utility, or happiness, from money is proportional to the logarithm of the amount of the money.
Under this assumption, if you increase or decrease any two people's wealth by the same percentage, other than an initial wealth of zero, then they both experience the same change in happiness. For example, if Jim's wealth suddenly increases from $1,000 to $1,100 and John's wealth suddenly increases from $10,000,000 to $11,000,000 they both experience the same increase in happiness, because in both cases their wealth increased by 10%.
Assuming that the happiness from money is indeed proportional to the log of the amount, then the following table shows the most somebody should be willing to pay according to his wealth before paying to play.
Indifference Amount to Play
| Wealth | Indifference Amount |
|---|---|
| $ 10 | $ 4.97 |
| $ 100 | $ 7.79 |
| $ 1,000 | $ 10.96 |
| $ 10,000 | $ 14.26 |
| $ 100,000 | $ 17.78 |
| $ 1,000,000 | $ 20.88 |
| $ 10,000,000 | $ 24.19 |
| $ 100,000,000 | $ 27.51 |
| $ 1,000,000,000 | $ 30.84 |
As you can see, under realistic conditions, the amount you should pay is much less than $∞. For example, if your wealth is one million dollars, then you should be indifferent to playing at a cost of $20.88.
This question is raised and discussed on my forum at Wizard of Vegas.
The Michigan Lottery has a three-player game with the following rules: Is there any positional advantage to going last in this game? What is the optimal strategy for each player? Here is a YouTube video showing the game.
First, there is no positional advantage to acting last. Since the players are kept in a sound-proof booth while any previous players play, order doesn't matter.
Second, there must be a Nash Equilibrium to the game where a strategy to stand with a score of at least x points will be superior to any other strategy. The question is finding x.
What I did was ask myself what would be the strategy if instead of a card numbered 1 to 100, each player got a random number uniformly distributed between 0 and 1 and look for the point x where a perfect logician would be indifferent between standing and switching. With that answer, it is easy to apply the answer to a discrete distribution from 1 to 100.
I'll stop talking at this point and let my readers enjoy the problem. See the links below for the answer and solution.
Answer for a continuous distribution from 0 to 1.
Answer for a discrete distribution from 1 to 100.
For my solution, please click here (PDF).
This question was raised and discussed in my forum at Wizard of Vegas.
Suppose you have a deck of ten red cards and ten black cards. After a random shuffle, you draw cards without replacement. What is the probability of drawing all ten black cards before five red cards?
That is the same as asking what is the probability that 14 random cards contain all 10 black cards. There are combin(10,4)=210 ways to choose 4 red cards out of the 10 in the deck. There is of course only one way to choose all ten black cards. There are combin(20,14)=38,760 ways to choose 14 cards out of 20. So the answer is 210/38,760=0.005418, or 1 in 184.57.
I know of a promotion that pays a bonus after achieving a four of a kind in all 13 ranks. How many hands will this take on average?
Let's look at the gold standard of video poker, 9-6 Jacks or Better to answer your question.
The first step is to modify my calculator to include a line item for all 13 four of a kinds. Here is that modified return table:
Modified Jacks or Better Return Table
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | 800 | 493,512,264 | 0.000025 | 0.019807 |
| Straight flush | 50 | 2,178,883,296 | 0.000109 | 0.005465 |
| Four A | 25 | 3,900,253,596 | 0.000196 | 0.004892 |
| Four K | 25 | 3,904,533,816 | 0.000196 | 0.004897 |
| Four Q | 25 | 3,898,370,196 | 0.000196 | 0.004889 |
| Four J | 25 | 3,886,872,684 | 0.000195 | 0.004875 |
| Four 10 | 25 | 3,471,687,732 | 0.000174 | 0.004354 |
| Four 9 | 25 | 3,503,226,684 | 0.000176 | 0.004394 |
| Four 8 | 25 | 3,504,128,652 | 0.000176 | 0.004395 |
| Four 7 | 25 | 3,504,825,252 | 0.000176 | 0.004396 |
| Four 6 | 25 | 3,504,861,888 | 0.000176 | 0.004396 |
| Four 5 | 25 | 3,504,895,944 | 0.000176 | 0.004396 |
| Four 4 | 25 | 3,504,032,676 | 0.000176 | 0.004395 |
| Four 3 | 25 | 3,503,177,148 | 0.000176 | 0.004394 |
| Four 2 | 25 | 3,502,301,496 | 0.000176 | 0.004393 |
| Full house | 9 | 229,475,482,596 | 0.011512 | 0.103610 |
| Flush | 6 | 219,554,786,160 | 0.011015 | 0.066087 |
| Straight | 4 | 223,837,565,784 | 0.011229 | 0.044917 |
| Three of a kind | 3 | 1,484,003,070,324 | 0.074449 | 0.223346 |
| Two pair | 2 | 2,576,946,164,148 | 0.129279 | 0.258558 |
| Jacks or better | 1 | 4,277,372,890,968 | 0.214585 | 0.214585 |
| Nothing | 0 | 10,872,274,993,896 | 0.545435 | 0.000000 |
| Total | 19,933,230,517,200 | 1.000000 | 0.995439 |
The probability of getting any four of a kind is 0.002363.
The next question to be answered is how many four of a kinds will take on average to get all 13 kinds? To answer that question, I created my Expected Trials Calculator. To use it, enter the number of combinations of each four of a kind in the first 13 cells. The calculator will tell you that it will take an expected 41.532646 four of a kinds to get all 13 kinds.
So, the expected number of hands played to get all 13 four of a kinds is 41.341739/0.002363 = 17,580.
A field of grass can feed exactly:
One cow and one llama for 21 days.
One llama and one sheep for 42 days.
One sheep and one cow for 28 days.
The cow eats as much grass as the llama and the sheep together.
The grass grows at a constant rate.
How long will it take the three animals together to totally devour the field of grass?
c = rate cow eats grass
l = rate llama eats grass
s = rate sheep eats grass
g = rate grass grows
At the end of a period of time, grass consumed must equal the initial amount of grass plus the amount of grass grown in that time. So...
(1) 21*(c+l) = 1 + 21g
(2) 42*(l+s) = 1+42g
(3) 28*(s+c) = 1+28g
Where the 1 represents one field of grass.
We are also given:
(4) c=s+l
First, substitute equation (4) into (2):
(5) 42c = 1 + 42g
Express that in terms of g:
(6) g = (42c-1)/42
Next, substitute equation (6) into (1)...
(7) 21(c+l) = 1 + 21*(42c-1)/42
After a little algebra we get...
(8) l = 1/42.
Next, substitute equation (4) into (3)...
(9) 28*(2s + l) = 1+28g
We know l=1/42, so...
28*(2s + 1/42) = 1+28g
56s + 28/42 = 1 + 28g
2352s + 28 = 42 + 1176g
(10) g = (2352s - 14)/1176
Next, substitute equation (8) and (10) into (2) ...
42*(1/42 + s) = 1 + 42*(2352s - 14)/1176
After some easy algebra we get:
(11) s = 14/1176 = 1/84
From equation (4)
(12) c = (1/84) + (1/42) = 3/84 = 1/28
So, if the grass didn't grow, then it would take the cow 28 days to eat the field, the llama 42, and the sheep 84.
Next, let's solve for g. Substitute (11) into (10):
g = [2352*(1/84)- 14]/1176
(13) g = 14/1176 = 1/84.
This is coincidentally the same rate the sheep eats the grass.
Let t be the final answer. We know that in t days the amount of grass eaten must equal the amount of grass in the field (1) plus the grass grown in that time. So...
(13) t*(s+l+c) = 1 + tg
Solving for t...
t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14) t = 84/5 = 16.8 days = 16 days, 19 hours, 12 minutes
This question was raised and discussed in my forum at Wizard of Vegas.
What is the mean distance between two random points in a unit square?
For a question so easy to ask, the solution is rather involved. The way I did it, you will need to know this integral.
Here is the answer and my solution (PDF).
What was the math problem on the chalkboard in the movie Good Will Hunting?
It was actually rather easy, especially for a course in combinatorial mathematics at MIT. Here is the wording of the problem:
"Draw all homeomorphically irreducible trees of size n=10."
Here is my attempt to put it in plain and simple English.
Using only straight lines, draw all figures where the sum of intersections and dead ends equals 10. You may not have any closed loops. You may also not have two equivalent figures. Any intersection must have at least three paths leading from it.
What do I mean by "equivalent," you might ask? It means you can move the pieces, while leaving the intersections alone, any way you wish and it won't create any new figures.
Here is an example:
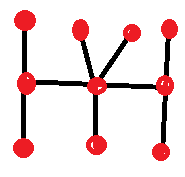
I'll give you a hint. Unlike the answer in the movie, there are ten of them. Will got only eight of them. See if you can match or beat Will Hunting.
- MATHEMATICS IN GOOD WILL HUNTING II: PROBLEMS FROM THE STUDENTS PERSPECTIVE -- Academic paper on the problem.
- THE GOOD WILL HUNTING MATH PROBLEM -- Discussion about the problem in my forum.
Consider a game with the following rules:
- A random number generator provides random numbers between 0 and 1 uniformly distributed.
- Two players each get a separate number. Each player can see his own number only.
- Player 1 may keep his initial number or swap for a new random number.
- Player 2, knowing player 1's action, has the same option to keep his original number or swap for a new one.
- Player with the higher number wins.
I have four questions about the game:
- Answer the following questions about the game:
- At what number is player 1 indifferent to standing and switching?
- Assuming player 1 switches, at what number should player 2 be indifferent to standing and switching?
- Assuming player 1 stands, at what number should player 2 be indifferent to standing and switching?
- Assuming optimal strategy by both players, what is the probability player 1 will win?
The answer and solution can be found in my page of Math Problems, problem 225.
I'm participating in a 2018 "dead pool." Here are the rules:
- Each player must submit a list of ten living celebrities under age 100.
- If any celebrity dies, as evidenced by a mention by the Associated Press, in 2018, then anyone with the celebrity's name on his list will receive 100-x points, where x is the age at death.
- Player with the most points on 1/1/2019 wins.
Going off of averages, what is the optimal strategy for this game?
As a former actuary, you asked the right person. Hopefully the Society of Actuaries will not consider my answer an abuse of the profession. That said, to answer your question I consulted a 2014 Period Life Table from my former place of work, the Office of the Chief Actuary of the Social Security Administration.
A period life table shows, among other things, the probability of death for a person of any given age and gender in 2014. Using that information I created the following table, which shows both the probability of death and expected points for all ages from 0 to 100 and both genders.
2014 Period Life Table Death Pool
| Age | Probability of Death — Male |
Probability of Death — Female |
Expected Points — Male |
Expected Points — Female |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
The table shows that the maximum expected points is for a 90 year-old-man at 1.645220.
This question is raised and discussed in my non-gambling forum, Diversity Tomorrow.
If you want to enclose 355 milliliters in a can, what should the dimensions be to minimize the surface area?
Good question! I was just wondering this when I saw some skinny soda cans at a gaming show, which held the usual 355 milliliters that the standard size does. Surely both can't be right (and don't call me Shirley).
r = radius of the can
h = height of the can
v = volume of the can
s= surface area of can
We know from simple geometry that the surface area = 2*pi*r^2 + 2*pi*r*h.
Likewise, we also know the volume is pi*r^2*h, which we're given equals 355.
So, 355=pi*r^2*h.
Let's rearrange that to:
(1) h = 355/(pi*r^2)
We know:
(2) s = 2*pi*r^2 + 2*pi*r*h.
Let's get that to a function of just one variable by substitute our expression for h in equation (1) into (2):
s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r.
Let's take the derivative of s and set it equal to zero, to solve for the optimal r.
ds/dr = 4*pi*r - 710/(r^2 ) = 0
4*pi*r = 710/(r^2)
Multiplying both sides by r^2:
4*pi*r^3 = 710
r^3 = 177.5/pi.
r = (177.5/pi)^(1/3) = 3.837215248.
Plug that value into equation (1) to get h = 7.674430496.
This question is raised and discussed in my forum at Wizard of Vegas.
It seems to me that most gambling professionals I know prefer to know a game’s volatility expressed as variance rather than as standard deviation. Of course, the former is just the square of the latter. However, I prefer the standard deviation since it is in the same units as the bet and win/loss. Perhaps they like a bigger number to make a bigger volatility stand out? What is your take – is there a preference for using "variance" by gamblers and, if so, why?
I agree that you hear the variance of a game bandied around more than it's standard deviation, which I have always found a little annoying. The reason I think gamblers should care about the volatility of a game is to associate a win or loss to a probability for a session of plays. For example, what would be a 1% bad loss after 200 hands of blackjack. To answer that, you would use the standard deviation of blackjack, which is about 1.15, depending on the rules.
The specific answer to that question is 1.15 × 200^0.5 × -2.32635 (which is the 1% point on the Gaussian curve) = -37.83 units south of expectations. Don't forget that due to the house edge you can expect to lose something. If we assume a house edge of 0.3%, then after 200 hands you could expect to lose 0.003*200 = 0.6 hands. So a 1% bad loss would be 0.6 + 37.83 = 38.43 hands.
I've heard the probability of a marriage ending in divorce, generally quoted as 50% in the United States, is calculated as the number of divorces to the number of marriages in the same period of time. Is that true? Do you think that is fair way to calculate the statistic? I question it because you're looking at divorces over a short time compared to marriages performed over a long time.
If the population and age distribution were stable, then if the divorce probability was truly 50%, then we would expect to see a ratio of one divorce to two marriages in any given period of time, given a large sample size.
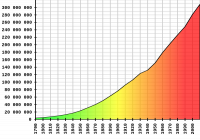
However, the population isn't stable. From this graph, it looks like the U.S. population is growing by 10.71% per decade. That comes to 1.02% per year. Let's just say 1% to keep it simple.
Map source: U.S. Census
According to fatherly.com, the average length of an unsuccessful marriage is 8 years.
If you were observing a 1 to 2 ratio of divorces to marriages in the present, what would be the average probability that any given marriage ends in divorce?
The divorces we're seeing now were from marriages 8 years ago, when the population was 92.35% what it is now. Simple math suggests the true probability of divorce is 54.14%.
Let's check that.
First, according to the CDC, there are 6.9 marriages to 1000 in population per year. This figure is not relevant to the question at hand, but I think helps see the numbers involved.
Suppose the population 8 years ago was 300,000,000. That would be 0.69% * 300 million = 2,070,000 marriages in that year.
If 54.14% of them end in divorce eight years later, then we would be seeing 2,070,000 * 54.14% = 1,120,698 divorces in the present.
1,120,698 / 2,070,000 = 50% observed ratio of divorces to marriages in the present.
Lest anyone say it, yes, I know that not all divorces end in exactly eight years. However, all things considered, I say that the bottom line won't be far from my 54.14% true divorce rate.
This question is raised and discussed in my forum at Wizard of Vegas.
Your office of 100 workers does a Secret Santa gift exchange. This where you write down everybody's name on individual pieces of paper, put them in a hat, and everybody draws a name at random to give a gift to.
The question is, how many closed loops will there be, on average? For example of a closed loop, Gordon gives to Don, who gives to Jon, who gives to Nathan, who gives to Gordon. Or drawing your own name.
Consider everybody choosing one at a time. As each person picks, there will be two types of situations:
- The name of the one picking has already been picked.
- The name of the one picking is still in the bin of names.
For any given picker, let's say there are n people left to pick.
If the name of the one picking has already been picked, there is a 1/n chance that the picker will choose close a loop involving his name. For example, let's say Amy is picking. Amy's name is already held by Bob, Bob's name is already held by Charlie, and Charlie's name is still in the bin. With n names still in the bin, there is a 1/n chance that Amy picks Charlie's name, closing a loop.
If the name of the one picking has not already been picked, there is a 1/n chance Amy picks her own name, closing a loop.
Either way, if the picker doesn't close a loop, she is joining part of another chain, which will eventually be closed by somebody else. Each chain should be counted once only, when it gets closed.
Thus the answer is 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
An estimate for any sufficiently large number of players, n, is ln(n).
The question is asked and discussed in my forum at Wizard of Vegas.
In honor of Ask the Wizard column #314, what are your favorite infinite series that sum to some function of pi?
It is easy to choose these two, as probably the two most famous:
- 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
- 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6
I've heard that with 23 random people, the probability of at least one common birthday to two or more people is over 50%? This this true? What is the probability of a common birthday for other group sizes? The same question also for a common birthday to 3, 4, and 5 people.
That is true, with 23 random people, the probability of at least one pair of people have a common birthday is 50.73%. This ignores leap day and assumes everybody has an equal chance of being born on each of the other 365 days (which is not actually the case, spring and fall birthdays are slightly more common).
The tables in answer to your question are quote long, so I'll put them in spoiler tags. Click on the buttons for the answers.
Common Birthday to 2+ People
| Group Size | Probability |
|---|---|
| 2 | 0.002740 |
| 3 | 0.008204 |
| 4 | 0.016356 |
| 5 | 0.027136 |
| 6 | 0.040462 |
| 7 | 0.056236 |
| 8 | 0.074335 |
| 9 | 0.094624 |
| 10 | 0.116948 |
| 11 | 0.141141 |
| 12 | 0.167025 |
| 13 | 0.194410 |
| 14 | 0.223103 |
| 15 | 0.252901 |
| 16 | 0.283604 |
| 17 | 0.315008 |
| 18 | 0.346911 |
| 19 | 0.379119 |
| 20 | 0.411438 |
| 21 | 0.443688 |
| 22 | 0.475695 |
| 23 | 0.507297 |
| 24 | 0.538344 |
| 25 | 0.568700 |
| 26 | 0.598241 |
| 27 | 0.626859 |
| 28 | 0.654461 |
| 29 | 0.680969 |
| 30 | 0.706316 |
| 31 | 0.730455 |
| 32 | 0.753348 |
| 33 | 0.774972 |
| 34 | 0.795317 |
| 35 | 0.814383 |
| 36 | 0.832182 |
| 37 | 0.848734 |
| 38 | 0.864068 |
| 39 | 0.878220 |
| 40 | 0.891232 |
| 41 | 0.903152 |
| 42 | 0.914030 |
| 43 | 0.923923 |
| 44 | 0.932885 |
| 45 | 0.940976 |
| 46 | 0.948253 |
| 47 | 0.954774 |
| 48 | 0.960598 |
| 49 | 0.965780 |
| 50 | 0.970374 |
| 51 | 0.974432 |
| 52 | 0.978005 |
| 53 | 0.981138 |
| 54 | 0.983877 |
| 55 | 0.986262 |
| 56 | 0.988332 |
| 57 | 0.990122 |
| 58 | 0.991665 |
| 59 | 0.992989 |
| 60 | 0.994123 |
| 61 | 0.995089 |
| 62 | 0.995910 |
| 63 | 0.996604 |
| 64 | 0.997190 |
| 65 | 0.997683 |
| 66 | 0.998096 |
| 67 | 0.998440 |
| 68 | 0.998726 |
| 69 | 0.998964 |
| 70 | 0.999160 |
| 71 | 0.999321 |
| 72 | 0.999453 |
| 73 | 0.999561 |
| 74 | 0.999649 |
| 75 | 0.999720 |
| 76 | 0.999777 |
| 77 | 0.999824 |
| 78 | 0.999861 |
| 79 | 0.999891 |
| 80 | 0.999914 |
| 81 | 0.999933 |
| 82 | 0.999948 |
| 83 | 0.999960 |
| 84 | 0.999969 |
Common Birthday to 3+ People
| Group Size | Probability |
|---|---|
| 3 | 0.000008 |
| 4 | 0.000030 |
| 5 | 0.000075 |
| 6 | 0.000149 |
| 7 | 0.000261 |
| 8 | 0.000416 |
| 9 | 0.000623 |
| 10 | 0.000888 |
| 11 | 0.001218 |
| 12 | 0.001621 |
| 13 | 0.002102 |
| 14 | 0.002670 |
| 15 | 0.003329 |
| 16 | 0.004088 |
| 17 | 0.004953 |
| 18 | 0.005929 |
| 19 | 0.007024 |
| 20 | 0.008243 |
| 21 | 0.009592 |
| 22 | 0.011078 |
| 23 | 0.012705 |
| 24 | 0.014481 |
| 25 | 0.016409 |
| 26 | 0.018497 |
| 27 | 0.020747 |
| 28 | 0.023167 |
| 29 | 0.025760 |
| 30 | 0.028531 |
| 31 | 0.031484 |
| 32 | 0.034624 |
| 33 | 0.037954 |
| 34 | 0.041479 |
| 35 | 0.045202 |
| 36 | 0.049126 |
| 37 | 0.053254 |
| 38 | 0.057589 |
| 39 | 0.062133 |
| 40 | 0.066889 |
| 41 | 0.071859 |
| 42 | 0.077044 |
| 43 | 0.082446 |
| 44 | 0.088065 |
| 45 | 0.093903 |
| 46 | 0.099960 |
| 47 | 0.106236 |
| 48 | 0.112731 |
| 49 | 0.119444 |
| 50 | 0.126375 |
| 51 | 0.133522 |
| 52 | 0.140885 |
| 53 | 0.148460 |
| 54 | 0.156246 |
| 55 | 0.164241 |
| 56 | 0.172441 |
| 57 | 0.180844 |
| 58 | 0.189445 |
| 59 | 0.198242 |
| 60 | 0.207230 |
| 61 | 0.216405 |
| 62 | 0.225761 |
| 63 | 0.235294 |
| 64 | 0.244999 |
| 65 | 0.254869 |
| 66 | 0.264899 |
| 67 | 0.275082 |
| 68 | 0.285413 |
| 69 | 0.295883 |
| 70 | 0.306487 |
| 71 | 0.317217 |
| 72 | 0.328066 |
| 73 | 0.339026 |
| 74 | 0.350088 |
| 75 | 0.361246 |
| 76 | 0.372491 |
| 77 | 0.383814 |
| 78 | 0.395207 |
| 79 | 0.406662 |
| 80 | 0.418169 |
| 81 | 0.429720 |
| 82 | 0.441307 |
| 83 | 0.452920 |
| 84 | 0.464550 |
| 85 | 0.476188 |
| 86 | 0.487826 |
| 87 | 0.499455 |
| 88 | 0.511065 |
| 89 | 0.522648 |
| 90 | 0.534196 |
| 91 | 0.545698 |
| 92 | 0.557148 |
| 93 | 0.568537 |
| 94 | 0.579855 |
| 95 | 0.591096 |
| 96 | 0.602252 |
| 97 | 0.613314 |
| 98 | 0.624275 |
| 99 | 0.635127 |
| 100 | 0.645865 |
| 101 | 0.656480 |
| 102 | 0.666967 |
| 103 | 0.677318 |
| 104 | 0.687529 |
| 105 | 0.697593 |
| 106 | 0.707505 |
| 107 | 0.717260 |
| 108 | 0.726853 |
| 109 | 0.736279 |
| 110 | 0.745536 |
| 111 | 0.754619 |
| 112 | 0.763525 |
| 113 | 0.772251 |
| 114 | 0.780795 |
| 115 | 0.789155 |
| 116 | 0.797330 |
| 117 | 0.805319 |
| 118 | 0.813121 |
| 119 | 0.820580 |
| 120 | 0.827964 |
| 121 | 0.835152 |
| 122 | 0.842144 |
| 123 | 0.848940 |
| 124 | 0.855540 |
| 125 | 0.861945 |
| 126 | 0.868155 |
| 127 | 0.874172 |
| 128 | 0.879996 |
| 129 | 0.885631 |
| 130 | 0.891076 |
| 131 | 0.896335 |
| 132 | 0.901409 |
| 133 | 0.906302 |
| 134 | 0.911015 |
| 135 | 0.915552 |
| 136 | 0.919915 |
| 137 | 0.924108 |
| 138 | 0.928135 |
| 139 | 0.931997 |
| 140 | 0.935700 |
| 141 | 0.939246 |
| 142 | 0.942640 |
| 143 | 0.945885 |
| 144 | 0.948985 |
| 145 | 0.951944 |
| 146 | 0.954766 |
| 147 | 0.957456 |
| 148 | 0.960016 |
| 149 | 0.962452 |
| 150 | 0.964767 |
| 151 | 0.966965 |
| 152 | 0.969050 |
| 153 | 0.971028 |
| 154 | 0.972900 |
| 155 | 0.974672 |
| 156 | 0.976347 |
| 157 | 0.977930 |
| 158 | 0.979423 |
| 159 | 0.980831 |
| 160 | 0.982158 |
| 161 | 0.983407 |
| 162 | 0.984581 |
| 163 | 0.985684 |
| 164 | 0.986719 |
| 165 | 0.987690 |
| 166 | 0.988600 |
| 167 | 0.989452 |
| 168 | 0.990248 |
| 169 | 0.990992 |
| 170 | 0.991687 |
| 171 | 0.992335 |
| 172 | 0.992938 |
| 173 | 0.993500 |
| 174 | 0.994022 |
| 175 | 0.994508 |
| 176 | 0.994958 |
| 177 | 0.995376 |
| 178 | 0.995763 |
| 179 | 0.996121 |
| 180 | 0.996452 |
| 181 | 0.996758 |
| 182 | 0.997040 |
| 183 | 0.997300 |
| 184 | 0.997540 |
| 185 | 0.997760 |
| 186 | 0.997963 |
| 187 | 0.998149 |
| 188 | 0.998319 |
| 189 | 0.998476 |
| 190 | 0.998619 |
| 191 | 0.998750 |
| 192 | 0.998869 |
| 193 | 0.998979 |
| 194 | 0.999078 |
| 195 | 0.999169 |
| 196 | 0.999251 |
| 197 | 0.999326 |
| 198 | 0.999394 |
| 199 | 0.999456 |
| 200 | 0.999512 |
| 201 | 0.999562 |
| 202 | 0.999608 |
| 203 | 0.999650 |
| 204 | 0.999687 |
| 205 | 0.999720 |
| 206 | 0.999751 |
| 207 | 0.999778 |
| 208 | 0.999802 |
| 209 | 0.999824 |
| 210 | 0.999844 |
| 211 | 0.999862 |
| 212 | 0.999877 |
| 213 | 0.999891 |
| 214 | 0.999904 |
| 215 | 0.999915 |
| 216 | 0.999925 |
| 217 | 0.999934 |
| 218 | 0.999942 |
| 219 | 0.999949 |
| 220 | 0.999955 |
| 221 | 0.999961 |
| 222 | 0.999966 |
| 223 | 0.999970 |
| 224 | 0.999974 |
| 225 | 0.999977 |
| 226 | 0.999980 |
| 227 | 0.999982 |
| 228 | 0.999985 |
| 229 | 0.999987 |
| 230 | 0.999988 |
| 231 | 0.999990 |
| 232 | 0.999991 |
| 233 | 0.999992 |
| 234 | 0.999994 |
| 235 | 0.999994 |
| 236 | 0.999995 |
| 237 | 0.999996 |
| 238 | 0.999996 |
| 239 | 0.999997 |
| 240 | 0.999997 |
| 241 | 0.999998 |
| 242 | 0.999998 |
| 243 | 0.999998 |
| 244 | 0.999999 |
Common Birthday to 4+ People
| Group Size | Probability |
|---|---|
| 4 | 0.000000 |
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000001 |
| 8 | 0.000001 |
| 9 | 0.000003 |
| 10 | 0.000004 |
| 11 | 0.000007 |
| 12 | 0.000010 |
| 13 | 0.000014 |
| 14 | 0.000020 |
| 15 | 0.000027 |
| 16 | 0.000036 |
| 17 | 0.000048 |
| 18 | 0.000061 |
| 19 | 0.000077 |
| 20 | 0.000096 |
| 21 | 0.000119 |
| 22 | 0.000145 |
| 23 | 0.000175 |
| 24 | 0.000209 |
| 25 | 0.000248 |
| 26 | 0.000293 |
| 27 | 0.000343 |
| 28 | 0.000399 |
| 29 | 0.000462 |
| 30 | 0.000532 |
| 31 | 0.000610 |
| 32 | 0.000695 |
| 33 | 0.000790 |
| 34 | 0.000893 |
| 35 | 0.001006 |
| 36 | 0.001129 |
| 37 | 0.001263 |
| 38 | 0.001408 |
| 39 | 0.001566 |
| 40 | 0.001736 |
| 41 | 0.001919 |
| 42 | 0.002116 |
| 43 | 0.002328 |
| 44 | 0.002555 |
| 45 | 0.002798 |
| 46 | 0.003058 |
| 47 | 0.003334 |
| 48 | 0.003629 |
| 49 | 0.003943 |
| 50 | 0.004276 |
| 51 | 0.004629 |
| 52 | 0.005003 |
| 53 | 0.005399 |
| 54 | 0.005817 |
| 55 | 0.006258 |
| 56 | 0.006724 |
| 57 | 0.007214 |
| 58 | 0.007730 |
| 59 | 0.008272 |
| 60 | 0.008841 |
| 61 | 0.009439 |
| 62 | 0.010065 |
| 63 | 0.010721 |
| 64 | 0.011408 |
| 65 | 0.012126 |
| 66 | 0.012876 |
| 67 | 0.013659 |
| 68 | 0.014476 |
| 69 | 0.015327 |
| 70 | 0.016215 |
| 71 | 0.017139 |
| 72 | 0.018100 |
| 73 | 0.019099 |
| 74 | 0.020137 |
| 75 | 0.021215 |
| 76 | 0.022334 |
| 77 | 0.023495 |
| 78 | 0.024698 |
| 79 | 0.025944 |
| 80 | 0.027235 |
| 81 | 0.028570 |
| 82 | 0.029951 |
| 83 | 0.031379 |
| 84 | 0.032855 |
| 85 | 0.034379 |
| 86 | 0.035952 |
| 87 | 0.037575 |
| 88 | 0.039249 |
| 89 | 0.040974 |
| 90 | 0.042752 |
| 91 | 0.044583 |
| 92 | 0.046467 |
| 93 | 0.048407 |
| 94 | 0.050402 |
| 95 | 0.052453 |
| 96 | 0.054561 |
| 97 | 0.056726 |
| 98 | 0.058950 |
| 99 | 0.061233 |
| 100 | 0.063576 |
| 101 | 0.065978 |
| 102 | 0.068442 |
| 103 | 0.070967 |
| 104 | 0.073554 |
| 105 | 0.076204 |
| 106 | 0.078917 |
| 107 | 0.081694 |
| 108 | 0.084535 |
| 109 | 0.087441 |
| 110 | 0.090412 |
| 111 | 0.093449 |
| 112 | 0.096552 |
| 113 | 0.099722 |
| 114 | 0.102958 |
| 115 | 0.106262 |
| 116 | 0.109633 |
| 117 | 0.113072 |
| 118 | 0.116579 |
| 119 | 0.120154 |
| 120 | 0.123798 |
| 121 | 0.127510 |
| 122 | 0.131292 |
| 123 | 0.135142 |
| 124 | 0.139061 |
| 125 | 0.143050 |
| 126 | 0.147107 |
| 127 | 0.151234 |
| 128 | 0.155429 |
| 129 | 0.159694 |
| 130 | 0.164027 |
| 131 | 0.168429 |
| 132 | 0.172899 |
| 133 | 0.177438 |
| 134 | 0.182044 |
| 135 | 0.186719 |
| 136 | 0.191460 |
| 137 | 0.196269 |
| 138 | 0.201144 |
| 139 | 0.206085 |
| 140 | 0.211091 |
| 141 | 0.216163 |
| 142 | 0.221299 |
| 143 | 0.226499 |
| 144 | 0.231763 |
| 145 | 0.237089 |
| 146 | 0.242476 |
| 147 | 0.247925 |
| 148 | 0.253434 |
| 149 | 0.259002 |
| 150 | 0.264629 |
| 151 | 0.270314 |
| 152 | 0.276055 |
| 153 | 0.281852 |
| 154 | 0.287703 |
| 155 | 0.293608 |
| 156 | 0.299566 |
| 157 | 0.305575 |
| 158 | 0.311634 |
| 159 | 0.317741 |
| 160 | 0.323897 |
| 161 | 0.330099 |
| 162 | 0.336346 |
| 163 | 0.342637 |
| 164 | 0.348970 |
| 165 | 0.355343 |
| 166 | 0.361757 |
| 167 | 0.368208 |
| 168 | 0.374696 |
| 169 | 0.381218 |
| 170 | 0.387774 |
| 171 | 0.394362 |
| 172 | 0.400980 |
| 173 | 0.407626 |
| 174 | 0.414299 |
| 175 | 0.420997 |
| 176 | 0.427718 |
| 177 | 0.434462 |
| 178 | 0.441224 |
| 179 | 0.448005 |
| 180 | 0.454803 |
| 181 | 0.461615 |
| 182 | 0.468439 |
| 183 | 0.475274 |
| 184 | 0.482118 |
| 185 | 0.488969 |
| 186 | 0.495826 |
| 187 | 0.502685 |
| 188 | 0.509546 |
| 189 | 0.516407 |
| 190 | 0.523265 |
| 191 | 0.530119 |
| 192 | 0.536967 |
| 193 | 0.543807 |
| 194 | 0.550636 |
| 195 | 0.557454 |
| 196 | 0.564258 |
| 197 | 0.571046 |
| 198 | 0.577817 |
| 199 | 0.584568 |
| 200 | 0.591298 |
| 201 | 0.598005 |
| 202 | 0.604687 |
| 203 | 0.611342 |
| 204 | 0.617969 |
| 205 | 0.624565 |
| 206 | 0.631129 |
| 207 | 0.637659 |
| 208 | 0.644154 |
| 209 | 0.650611 |
| 210 | 0.657030 |
| 211 | 0.663407 |
| 212 | 0.669743 |
| 213 | 0.676035 |
| 214 | 0.682281 |
| 215 | 0.688481 |
| 216 | 0.694632 |
| 217 | 0.700734 |
| 218 | 0.706784 |
| 219 | 0.712782 |
| 220 | 0.718726 |
| 221 | 0.724614 |
| 222 | 0.730446 |
| 223 | 0.736220 |
| 224 | 0.741936 |
| 225 | 0.747591 |
| 226 | 0.753185 |
| 227 | 0.758717 |
| 228 | 0.764185 |
| 229 | 0.769590 |
| 230 | 0.774929 |
| 231 | 0.780202 |
| 232 | 0.785409 |
| 233 | 0.790547 |
| 234 | 0.795618 |
| 235 | 0.800619 |
| 236 | 0.805551 |
| 237 | 0.810412 |
| 238 | 0.815202 |
| 239 | 0.819921 |
| 240 | 0.824569 |
| 241 | 0.829144 |
| 242 | 0.833646 |
| 243 | 0.838076 |
| 244 | 0.842432 |
| 245 | 0.846716 |
| 246 | 0.850925 |
| 247 | 0.855061 |
| 248 | 0.859123 |
| 249 | 0.863112 |
| 250 | 0.867027 |
| 251 | 0.870868 |
| 252 | 0.874635 |
| 253 | 0.878329 |
| 254 | 0.881950 |
| 255 | 0.885498 |
| 256 | 0.888973 |
| 257 | 0.892375 |
| 258 | 0.895705 |
| 259 | 0.898964 |
| 260 | 0.902151 |
| 261 | 0.905268 |
| 262 | 0.908314 |
| 263 | 0.911290 |
| 264 | 0.914197 |
| 265 | 0.917036 |
| 266 | 0.919806 |
| 267 | 0.922509 |
| 268 | 0.925145 |
| 269 | 0.927715 |
| 270 | 0.930220 |
| 271 | 0.932661 |
| 272 | 0.935037 |
| 273 | 0.937351 |
| 274 | 0.939603 |
| 275 | 0.941793 |
| 276 | 0.943923 |
| 277 | 0.945993 |
| 278 | 0.948005 |
| 279 | 0.949960 |
| 280 | 0.951857 |
| 281 | 0.953699 |
| 282 | 0.955486 |
| 283 | 0.957218 |
| 284 | 0.958898 |
| 285 | 0.960527 |
| 286 | 0.962104 |
| 287 | 0.963631 |
| 288 | 0.965109 |
| 289 | 0.966540 |
| 290 | 0.967923 |
| 291 | 0.969260 |
| 292 | 0.970553 |
| 293 | 0.971802 |
| 294 | 0.973007 |
| 295 | 0.974171 |
| 296 | 0.975294 |
| 297 | 0.976377 |
| 298 | 0.977421 |
| 299 | 0.978427 |
| 300 | 0.979397 |
| 301 | 0.980330 |
| 302 | 0.981228 |
| 303 | 0.982092 |
| 304 | 0.982923 |
| 305 | 0.983722 |
| 306 | 0.984490 |
| 307 | 0.985227 |
| 308 | 0.985935 |
| 309 | 0.986614 |
| 310 | 0.987266 |
| 311 | 0.987890 |
| 312 | 0.988489 |
| 313 | 0.989063 |
| 314 | 0.989612 |
| 315 | 0.990138 |
| 316 | 0.990641 |
| 317 | 0.991122 |
| 318 | 0.991581 |
| 319 | 0.992021 |
| 320 | 0.992440 |
| 321 | 0.992841 |
| 322 | 0.993223 |
| 323 | 0.993587 |
| 324 | 0.993935 |
| 325 | 0.994266 |
| 326 | 0.994581 |
| 327 | 0.994882 |
| 328 | 0.995167 |
| 329 | 0.995439 |
| 330 | 0.995698 |
| 331 | 0.995943 |
| 332 | 0.996176 |
| 333 | 0.996398 |
| 334 | 0.996608 |
| 335 | 0.996807 |
| 336 | 0.996996 |
| 337 | 0.997175 |
| 338 | 0.997344 |
| 339 | 0.997505 |
| 340 | 0.997657 |
| 341 | 0.997801 |
| 342 | 0.997936 |
| 343 | 0.998065 |
| 344 | 0.998186 |
| 345 | 0.998300 |
| 346 | 0.998408 |
| 347 | 0.998510 |
| 348 | 0.998606 |
| 349 | 0.998696 |
| 350 | 0.998781 |
| 351 | 0.998861 |
| 352 | 0.998937 |
| 353 | 0.999008 |
| 354 | 0.999074 |
| 355 | 0.999137 |
| 356 | 0.999195 |
| 357 | 0.999250 |
| 358 | 0.999302 |
| 359 | 0.999350 |
| 360 | 0.999396 |
| 361 | 0.999438 |
| 362 | 0.999478 |
| 363 | 0.999515 |
| 364 | 0.999550 |
| 365 | 0.999582 |
| 366 | 0.999613 |
| 367 | 0.999641 |
| 368 | 0.999668 |
| 369 | 0.999692 |
| 370 | 0.999715 |
| 371 | 0.999736 |
| 372 | 0.999756 |
| 373 | 0.999775 |
| 374 | 0.999792 |
| 375 | 0.999808 |
| 376 | 0.999823 |
| 377 | 0.999837 |
| 378 | 0.999850 |
| 379 | 0.999861 |
| 380 | 0.999872 |
| 381 | 0.999883 |
| 382 | 0.999892 |
| 383 | 0.999901 |
| 384 | 0.999909 |
| 385 | 0.999916 |
| 386 | 0.999923 |
| 387 | 0.999930 |
| 388 | 0.999935 |
| 389 | 0.999941 |
| 390 | 0.999946 |
| 391 | 0.999950 |
| 392 | 0.999955 |
| 393 | 0.999959 |
| 394 | 0.999962 |
| 395 | 0.999965 |
| 396 | 0.999969 |
| 397 | 0.999971 |
| 398 | 0.999974 |
| 399 | 0.999976 |
| 400 | 0.999978 |
| 401 | 0.999980 |
| 402 | 0.999982 |
| 403 | 0.999984 |
| 404 | 0.999985 |
| 405 | 0.999987 |
| 406 | 0.999988 |
| 407 | 0.999989 |
| 408 | 0.999990 |
| 409 | 0.999991 |
| 410 | 0.999992 |
| 411 | 0.999993 |
| 412 | 0.999993 |
| 413 | 0.999994 |
| 414 | 0.999995 |
| 415 | 0.999995 |
| 416 | 0.999996 |
| 417 | 0.999996 |
| 418 | 0.999996 |
| 419 | 0.999997 |
| 420 | 0.999997 |
| 421 | 0.999997 |
| 422 | 0.999998 |
| 423 | 0.999998 |
| 424 | 0.999998 |
| 425 | 0.999998 |
| 426 | 0.999998 |
| 427 | 0.999999 |
| 428 | 0.999999 |
| 429 | 0.999999 |
Common Birthday to 5+ People
| Group Size | Probability |
|---|---|
| 5 | 0.000000 |
| 6 | 0.000000 |
| 7 | 0.000000 |
| 8 | 0.000000 |
| 9 | 0.000000 |
| 10 | 0.000000 |
| 11 | 0.000000 |
| 12 | 0.000000 |
| 13 | 0.000000 |
| 14 | 0.000000 |
| 15 | 0.000000 |
| 16 | 0.000000 |
| 17 | 0.000000 |
| 18 | 0.000001 |
| 19 | 0.000001 |
| 20 | 0.000001 |
| 21 | 0.000001 |
| 22 | 0.000002 |
| 23 | 0.000002 |
| 24 | 0.000003 |
| 25 | 0.000004 |
| 26 | 0.000004 |
| 27 | 0.000005 |
| 28 | 0.000006 |
| 29 | 0.000008 |
| 30 | 0.000009 |
| 31 | 0.000011 |
| 32 | 0.000013 |
| 33 | 0.000015 |
| 34 | 0.000017 |
| 35 | 0.000020 |
| 36 | 0.000023 |
| 37 | 0.000026 |
| 38 | 0.000030 |
| 39 | 0.000034 |
| 40 | 0.000039 |
| 41 | 0.000044 |
| 42 | 0.000050 |
| 43 | 0.000056 |
| 44 | 0.000063 |
| 45 | 0.000070 |
| 46 | 0.000079 |
| 47 | 0.000087 |
| 48 | 0.000097 |
| 49 | 0.000108 |
| 50 | 0.000119 |
| 51 | 0.000132 |
| 52 | 0.000145 |
| 53 | 0.000159 |
| 54 | 0.000175 |
| 55 | 0.000192 |
| 56 | 0.000209 |
| 57 | 0.000229 |
| 58 | 0.000249 |
| 59 | 0.000271 |
| 60 | 0.000295 |
| 61 | 0.000320 |
| 62 | 0.000347 |
| 63 | 0.000375 |
| 64 | 0.000406 |
| 65 | 0.000438 |
| 66 | 0.000472 |
| 67 | 0.000509 |
| 68 | 0.000547 |
| 69 | 0.000588 |
| 70 | 0.000631 |
| 71 | 0.000676 |
| 72 | 0.000725 |
| 73 | 0.000775 |
| 74 | 0.000829 |
| 75 | 0.000885 |
| 76 | 0.000944 |
| 77 | 0.001007 |
| 78 | 0.001072 |
| 79 | 0.001141 |
| 80 | 0.001213 |
| 81 | 0.001289 |
| 82 | 0.001369 |
| 83 | 0.001452 |
| 84 | 0.001539 |
| 85 | 0.001630 |
| 86 | 0.001726 |
| 87 | 0.001825 |
| 88 | 0.001930 |
| 89 | 0.002038 |
| 90 | 0.002152 |
| 91 | 0.002270 |
| 92 | 0.002394 |
| 93 | 0.002522 |
| 94 | 0.002656 |
| 95 | 0.002796 |
| 96 | 0.002941 |
| 97 | 0.003092 |
| 98 | 0.003249 |
| 99 | 0.003412 |
| 100 | 0.003581 |
| 101 | 0.003757 |
| 102 | 0.003939 |
| 103 | 0.004128 |
| 104 | 0.004325 |
| 105 | 0.004528 |
| 106 | 0.004739 |
| 107 | 0.004957 |
| 108 | 0.005183 |
| 109 | 0.005417 |
| 110 | 0.005659 |
| 111 | 0.005909 |
| 112 | 0.006168 |
| 113 | 0.006436 |
| 114 | 0.006712 |
| 115 | 0.006998 |
| 116 | 0.007293 |
| 117 | 0.007597 |
| 118 | 0.007912 |
| 119 | 0.008236 |
| 120 | 0.008570 |
| 121 | 0.008915 |
| 122 | 0.009270 |
| 123 | 0.009636 |
| 124 | 0.010013 |
| 125 | 0.010402 |
| 126 | 0.010801 |
| 127 | 0.011213 |
| 128 | 0.011637 |
| 129 | 0.012072 |
| 130 | 0.012521 |
| 131 | 0.012981 |
| 132 | 0.013455 |
| 133 | 0.013942 |
| 134 | 0.014442 |
| 135 | 0.014956 |
| 136 | 0.015484 |
| 137 | 0.016026 |
| 138 | 0.016582 |
| 139 | 0.017153 |
| 140 | 0.017739 |
| 141 | 0.018340 |
| 142 | 0.018956 |
| 143 | 0.019588 |
| 144 | 0.020235 |
| 145 | 0.020899 |
| 146 | 0.021580 |
| 147 | 0.022277 |
| 148 | 0.022991 |
| 149 | 0.023722 |
| 150 | 0.024470 |
| 151 | 0.025237 |
| 152 | 0.026021 |
| 153 | 0.026824 |
| 154 | 0.027645 |
| 155 | 0.028485 |
| 156 | 0.029344 |
| 157 | 0.030222 |
| 158 | 0.031120 |
| 159 | 0.032037 |
| 160 | 0.032975 |
| 161 | 0.033934 |
| 162 | 0.034913 |
| 163 | 0.035912 |
| 164 | 0.036934 |
| 165 | 0.037976 |
| 166 | 0.039040 |
| 167 | 0.040127 |
| 168 | 0.041235 |
| 169 | 0.042367 |
| 170 | 0.043521 |
| 171 | 0.044698 |
| 172 | 0.045898 |
| 173 | 0.047122 |
| 174 | 0.048370 |
| 175 | 0.049642 |
| 176 | 0.050939 |
| 177 | 0.052260 |
| 178 | 0.053606 |
| 179 | 0.054977 |
| 180 | 0.056374 |
| 181 | 0.057796 |
| 182 | 0.059245 |
| 183 | 0.060719 |
| 184 | 0.062220 |
| 185 | 0.063748 |
| 186 | 0.065302 |
| 187 | 0.066884 |
| 188 | 0.068493 |
| 189 | 0.070130 |
| 190 | 0.071795 |
| 191 | 0.073487 |
| 192 | 0.075209 |
| 193 | 0.076958 |
| 194 | 0.078737 |
| 195 | 0.080544 |
| 196 | 0.082381 |
| 197 | 0.084247 |
| 198 | 0.086143 |
| 199 | 0.088068 |
| 200 | 0.090024 |
| 201 | 0.092009 |
| 202 | 0.094026 |
| 203 | 0.096072 |
| 204 | 0.098150 |
| 205 | 0.100259 |
| 206 | 0.102398 |
| 207 | 0.104569 |
| 208 | 0.106772 |
| 209 | 0.109006 |
| 210 | 0.111272 |
| 211 | 0.113570 |
| 212 | 0.115899 |
| 213 | 0.118262 |
| 214 | 0.120656 |
| 215 | 0.123083 |
| 216 | 0.125542 |
| 217 | 0.128035 |
| 218 | 0.130559 |
| 219 | 0.133117 |
| 220 | 0.135708 |
| 221 | 0.138332 |
| 222 | 0.140989 |
| 223 | 0.143679 |
| 224 | 0.146403 |
| 225 | 0.149160 |
| 226 | 0.151950 |
| 227 | 0.154774 |
| 228 | 0.157632 |
| 229 | 0.160522 |
| 230 | 0.163447 |
| 231 | 0.166405 |
| 232 | 0.169396 |
| 233 | 0.172421 |
| 234 | 0.175480 |
| 235 | 0.178572 |
| 236 | 0.181698 |
| 237 | 0.184857 |
| 238 | 0.188049 |
| 239 | 0.191275 |
| 240 | 0.194534 |
| 241 | 0.197827 |
| 242 | 0.201152 |
| 243 | 0.204511 |
| 244 | 0.207902 |
| 245 | 0.211327 |
| 246 | 0.214784 |
| 247 | 0.218274 |
| 248 | 0.221796 |
| 249 | 0.225351 |
| 250 | 0.228937 |
| 251 | 0.232556 |
| 252 | 0.236207 |
| 253 | 0.239889 |
| 254 | 0.243603 |
| 255 | 0.247348 |
| 256 | 0.251124 |
| 257 | 0.254931 |
| 258 | 0.258768 |
| 259 | 0.262636 |
| 260 | 0.266534 |
| 261 | 0.270462 |
| 262 | 0.274419 |
| 263 | 0.278406 |
| 264 | 0.282422 |
| 265 | 0.286466 |
| 266 | 0.290539 |
| 267 | 0.294639 |
| 268 | 0.298768 |
| 269 | 0.302924 |
| 270 | 0.307106 |
| 271 | 0.311316 |
| 272 | 0.315551 |
| 273 | 0.319813 |
| 274 | 0.324100 |
| 275 | 0.328412 |
| 276 | 0.332749 |
| 277 | 0.337110 |
| 278 | 0.341495 |
| 279 | 0.345903 |
| 280 | 0.350334 |
| 281 | 0.354788 |
| 282 | 0.359264 |
| 283 | 0.363761 |
| 284 | 0.368279 |
| 285 | 0.372818 |
| 286 | 0.377376 |
| 287 | 0.381955 |
| 288 | 0.386552 |
| 289 | 0.391167 |
| 290 | 0.395801 |
| 291 | 0.400452 |
| 292 | 0.405119 |
| 293 | 0.409803 |
| 294 | 0.414503 |
| 295 | 0.419217 |
| 296 | 0.423946 |
| 297 | 0.428689 |
| 298 | 0.433445 |
| 299 | 0.438214 |
| 300 | 0.442995 |
| 301 | 0.447787 |
| 302 | 0.452590 |
| 303 | 0.457403 |
| 304 | 0.462226 |
| 305 | 0.467057 |
| 306 | 0.471897 |
| 307 | 0.476744 |
| 308 | 0.481599 |
| 309 | 0.486459 |
| 310 | 0.491325 |
| 311 | 0.496196 |
| 312 | 0.501070 |
| 313 | 0.505949 |
| 314 | 0.510830 |
| 315 | 0.515713 |
| 316 | 0.520598 |
| 317 | 0.525483 |
| 318 | 0.530369 |
| 319 | 0.535253 |
| 320 | 0.540137 |
| 321 | 0.545018 |
| 322 | 0.549896 |
| 323 | 0.554771 |
| 324 | 0.559642 |
| 325 | 0.564507 |
| 326 | 0.569367 |
| 327 | 0.574221 |
| 328 | 0.579067 |
| 329 | 0.583906 |
| 330 | 0.588736 |
| 331 | 0.593557 |
| 332 | 0.598368 |
| 333 | 0.603169 |
| 334 | 0.607958 |
| 335 | 0.612735 |
| 336 | 0.617500 |
| 337 | 0.622251 |
| 338 | 0.626988 |
| 339 | 0.631710 |
| 340 | 0.636417 |
| 341 | 0.641107 |
| 342 | 0.645781 |
| 343 | 0.650437 |
| 344 | 0.655075 |
| 345 | 0.659695 |
| 346 | 0.664295 |
| 347 | 0.668875 |
| 348 | 0.673434 |
| 349 | 0.677972 |
| 350 | 0.682488 |
| 351 | 0.686981 |
| 352 | 0.691451 |
| 353 | 0.695897 |
| 354 | 0.700319 |
| 355 | 0.704716 |
| 356 | 0.709088 |
| 357 | 0.713433 |
| 358 | 0.717752 |
| 359 | 0.722043 |
| 360 | 0.726307 |
| 361 | 0.730543 |
| 362 | 0.734750 |
| 363 | 0.738927 |
| 364 | 0.743075 |
| 365 | 0.747193 |
| 366 | 0.751279 |
| 367 | 0.755335 |
| 368 | 0.759359 |
| 369 | 0.763351 |
| 370 | 0.767310 |
| 371 | 0.771237 |
| 372 | 0.775130 |
| 373 | 0.778990 |
| 374 | 0.782815 |
| 375 | 0.786606 |
| 376 | 0.790363 |
| 377 | 0.794084 |
| 378 | 0.797770 |
| 379 | 0.801420 |
| 380 | 0.805034 |
| 381 | 0.808611 |
| 382 | 0.812152 |
| 383 | 0.815656 |
| 384 | 0.819123 |
| 385 | 0.822553 |
| 386 | 0.825945 |
| 387 | 0.829300 |
| 388 | 0.832616 |
| 389 | 0.835895 |
| 390 | 0.839135 |
| 391 | 0.842336 |
| 392 | 0.845499 |
| 393 | 0.848624 |
| 394 | 0.851709 |
| 395 | 0.854756 |
| 396 | 0.857764 |
| 397 | 0.860733 |
| 398 | 0.863663 |
| 399 | 0.866553 |
| 400 | 0.869405 |
| 401 | 0.872217 |
| 402 | 0.874990 |
| 403 | 0.877724 |
| 404 | 0.880419 |
| 405 | 0.883075 |
| 406 | 0.885692 |
| 407 | 0.888269 |
| 408 | 0.890808 |
| 409 | 0.893309 |
| 410 | 0.895770 |
| 411 | 0.898193 |
| 412 | 0.900578 |
| 413 | 0.902924 |
| 414 | 0.905232 |
| 415 | 0.907502 |
| 416 | 0.909734 |
| 417 | 0.911929 |
| 418 | 0.914086 |
| 419 | 0.916205 |
| 420 | 0.918288 |
| 421 | 0.920334 |
| 422 | 0.922344 |
| 423 | 0.924317 |
| 424 | 0.926254 |
| 425 | 0.928155 |
| 426 | 0.930020 |
| 427 | 0.931851 |
| 428 | 0.933646 |
| 429 | 0.935406 |
| 430 | 0.937133 |
| 431 | 0.938825 |
| 432 | 0.940483 |
| 433 | 0.942108 |
| 434 | 0.943699 |
| 435 | 0.945258 |
| 436 | 0.946785 |
| 437 | 0.948279 |
| 438 | 0.949741 |
| 439 | 0.951173 |
| 440 | 0.952573 |
| 441 | 0.953942 |
| 442 | 0.955281 |
| 443 | 0.956590 |
| 444 | 0.957870 |
| 445 | 0.959120 |
| 446 | 0.960342 |
| 447 | 0.961535 |
| 448 | 0.962701 |
| 449 | 0.963838 |
| 450 | 0.964949 |
| 451 | 0.966032 |
| 452 | 0.967090 |
| 453 | 0.968121 |
| 454 | 0.969127 |
| 455 | 0.970107 |
| 456 | 0.971063 |
| 457 | 0.971994 |
| 458 | 0.972902 |
| 459 | 0.973785 |
| 460 | 0.974646 |
| 461 | 0.975484 |
| 462 | 0.976299 |
| 463 | 0.977093 |
| 464 | 0.977865 |
| 465 | 0.978616 |
| 466 | 0.979346 |
| 467 | 0.980056 |
| 468 | 0.980746 |
| 469 | 0.981416 |
| 470 | 0.982067 |
| 471 | 0.982699 |
| 472 | 0.983313 |
| 473 | 0.983909 |
| 474 | 0.984488 |
| 475 | 0.985049 |
| 476 | 0.985593 |
| 477 | 0.986121 |
| 478 | 0.986633 |
| 479 | 0.987128 |
| 480 | 0.987609 |
| 481 | 0.988074 |
| 482 | 0.988525 |
| 483 | 0.988962 |
| 484 | 0.989384 |
| 485 | 0.989793 |
| 486 | 0.990189 |
| 487 | 0.990571 |
| 488 | 0.990941 |
| 489 | 0.991299 |
| 490 | 0.991644 |
| 491 | 0.991978 |
| 492 | 0.992301 |
| 493 | 0.992612 |
| 494 | 0.992913 |
| 495 | 0.993203 |
| 496 | 0.993483 |
| 497 | 0.993753 |
| 498 | 0.994013 |
| 499 | 0.994264 |
| 500 | 0.994506 |
| 501 | 0.994740 |
| 502 | 0.994964 |
| 503 | 0.995180 |
| 504 | 0.995389 |
| 505 | 0.995589 |
| 506 | 0.995782 |
| 507 | 0.995967 |
| 508 | 0.996146 |
| 509 | 0.996317 |
| 510 | 0.996482 |
| 511 | 0.996640 |
| 512 | 0.996793 |
| 513 | 0.996939 |
| 514 | 0.997079 |
| 515 | 0.997213 |
| 516 | 0.997343 |
| 517 | 0.997466 |
| 518 | 0.997585 |
| 519 | 0.997699 |
| 520 | 0.997808 |
| 521 | 0.997913 |
| 522 | 0.998013 |
| 523 | 0.998109 |
| 524 | 0.998200 |
| 525 | 0.998288 |
| 526 | 0.998372 |
| 527 | 0.998452 |
| 528 | 0.998529 |
| 529 | 0.998602 |
| 530 | 0.998673 |
| 531 | 0.998739 |
| 532 | 0.998803 |
| 533 | 0.998864 |
| 534 | 0.998923 |
| 535 | 0.998978 |
| 536 | 0.999031 |
| 537 | 0.999082 |
| 538 | 0.999130 |
| 539 | 0.999176 |
| 540 | 0.999219 |
| 541 | 0.999261 |
| 542 | 0.999301 |
| 543 | 0.999338 |
| 544 | 0.999374 |
| 545 | 0.999408 |
| 546 | 0.999441 |
| 547 | 0.999471 |
| 548 | 0.999501 |
| 549 | 0.999528 |
| 550 | 0.999555 |
| 551 | 0.999580 |
| 552 | 0.999604 |
| 553 | 0.999626 |
| 554 | 0.999648 |
| 555 | 0.999668 |
| 556 | 0.999687 |
| 557 | 0.999705 |
| 558 | 0.999722 |
| 559 | 0.999739 |
| 560 | 0.999754 |
| 561 | 0.999769 |
| 562 | 0.999782 |
| 563 | 0.999795 |
| 564 | 0.999808 |
| 565 | 0.999819 |
| 566 | 0.999830 |
| 567 | 0.999841 |
| 568 | 0.999851 |
| 569 | 0.999860 |
| 570 | 0.999868 |
| 571 | 0.999877 |
| 572 | 0.999884 |
| 573 | 0.999892 |
| 574 | 0.999899 |
| 575 | 0.999905 |
| 576 | 0.999911 |
| 577 | 0.999917 |
| 578 | 0.999922 |
| 579 | 0.999927 |
| 580 | 0.999932 |
| 581 | 0.999936 |
| 582 | 0.999941 |
| 583 | 0.999945 |
| 584 | 0.999948 |
| 585 | 0.999952 |
| 586 | 0.999955 |
| 587 | 0.999958 |
| 588 | 0.999961 |
| 589 | 0.999964 |
| 590 | 0.999966 |
| 591 | 0.999968 |
| 592 | 0.999971 |
| 593 | 0.999973 |
| 594 | 0.999975 |
| 595 | 0.999976 |
| 596 | 0.999978 |
| 597 | 0.999980 |
| 598 | 0.999981 |
| 599 | 0.999982 |
| 600 | 0.999984 |
| 601 | 0.999985 |
| 602 | 0.999986 |
| 603 | 0.999987 |
| 604 | 0.999988 |
| 605 | 0.999989 |
| 606 | 0.999990 |
| 607 | 0.999990 |
| 608 | 0.999991 |
| 609 | 0.999992 |
| 610 | 0.999992 |
| 611 | 0.999993 |
| 612 | 0.999994 |
| 613 | 0.999994 |
| 614 | 0.999994 |
| 615 | 0.999995 |
| 616 | 0.999995 |
| 617 | 0.999996 |
| 618 | 0.999996 |
| 619 | 0.999996 |
| 620 | 0.999997 |
| 621 | 0.999997 |
| 622 | 0.999997 |
| 623 | 0.999997 |
| 624 | 0.999998 |
| 625 | 0.999998 |
| 626 | 0.999998 |
| 627 | 0.999998 |
| 628 | 0.999998 |
| 629 | 0.999998 |
| 630 | 0.999999 |
| 631 | 0.999999 |
| 632 | 0.999999 |
| 633 | 0.999999 |
| 634 | 0.999999 |
Let's say a dealer has chips of every denomination evenly divisible by $1. You buy in at the table for $10. How many different ways can the dealer give change for the $10? How about for other buy-in amounts?
There are 42 ways the dealer could break down $10. Here they are:
9,1
8,2
8,1,1
7,3
7,2,1
7,1,1,1
6,4
6,3,1
6,2,2
6,2,1,1
6,1,1,1,1
5,5
5,4,1
5,3,2
5,3,1,1
5,2,2,1
5,2,1,1,1
5,1,1,1,1,1
4,4,2
4,4,1,1
4,3,3
4,3,2,1
4,3,1,1,1
4,2,2,2
4,2,2,1,1
4,2,1,1,1,1
4,1,1,1,1,1,1
3,3,3,1
3,3,2,2
3,3,2,1,1
3,3,1,1,1,1
3,2,2,2,1
3,2,2,1,1,1
3,2,1,1,1,1,1
3,1,1,1,1,1,1,1
2,2,2,2,2
2,2,2,2,1,1
2,2,2,1,1,1,1
2,2,1,1,1,1,1,1
2,1,1,1,1,1,1,1,1
1,1,1,1,1,1,1,1,1,1
Mathematicians call these partitions. Here are the number of partitions for starting quantities up to 405, which is as high as my computer can calculate (2^64).
Common Birthday to 2+ People
| Initial Quantity |
Total Partitions |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 11 |
| 7 | 15 |
| 8 | 22 |
| 9 | 30 |
| 10 | 42 |
| 11 | 56 |
| 12 | 77 |
| 13 | 101 |
| 14 | 135 |
| 15 | 176 |
| 16 | 231 |
| 17 | 297 |
| 18 | 385 |
| 19 | 490 |
| 20 | 627 |
| 21 | 792 |
| 22 | 1002 |
| 23 | 1255 |
| 24 | 1575 |
| 25 | 1958 |
| 26 | 2436 |
| 27 | 3010 |
| 28 | 3718 |
| 29 | 4565 |
| 30 | 5604 |
| 31 | 6842 |
| 32 | 8349 |
| 33 | 10143 |
| 34 | 12310 |
| 35 | 14883 |
| 36 | 17977 |
| 37 | 21637 |
| 38 | 26015 |
| 39 | 31185 |
| 40 | 37338 |
| 41 | 44583 |
| 42 | 53174 |
| 43 | 63261 |
| 44 | 75175 |
| 45 | 89134 |
| 46 | 105558 |
| 47 | 124754 |
| 48 | 147273 |
| 49 | 173525 |
| 50 | 204226 |
| 51 | 239943 |
| 52 | 281589 |
| 53 | 329931 |
| 54 | 386155 |
| 55 | 451276 |
| 56 | 526823 |
| 57 | 614154 |
| 58 | 715220 |
| 59 | 831820 |
| 60 | 966467 |
| 61 | 1121505 |
| 62 | 1300156 |
| 63 | 1505499 |
| 64 | 1741630 |
| 65 | 2012558 |
| 66 | 2323520 |
| 67 | 2679689 |
| 68 | 3087735 |
| 69 | 3554345 |
| 70 | 4087968 |
| 71 | 4697205 |
| 72 | 5392783 |
| 73 | 6185689 |
| 74 | 7089500 |
| 75 | 8118264 |
| 76 | 9289091 |
| 77 | 10619863 |
| 78 | 12132164 |
| 79 | 13848650 |
| 80 | 15796476 |
| 81 | 18004327 |
| 82 | 20506255 |
| 83 | 23338469 |
| 84 | 26543660 |
| 85 | 30167357 |
| 86 | 34262962 |
| 87 | 38887673 |
| 88 | 44108109 |
| 89 | 49995925 |
| 90 | 56634173 |
| 91 | 64112359 |
| 92 | 72533807 |
| 93 | 82010177 |
| 94 | 92669720 |
| 95 | 104651419 |
| 96 | 118114304 |
| 97 | 133230930 |
| 98 | 150198136 |
| 99 | 169229875 |
| 100 | 190569292 |
| 101 | 214481126 |
| 102 | 241265379 |
| 103 | 271248950 |
| 104 | 304801365 |
| 105 | 342325709 |
| 106 | 384276336 |
| 107 | 431149389 |
| 108 | 483502844 |
| 109 | 541946240 |
| 110 | 607163746 |
| 111 | 679903203 |
| 112 | 761002156 |
| 113 | 851376628 |
| 114 | 952050665 |
| 115 | 1064144451 |
| 116 | 1188908248 |
| 117 | 1327710076 |
| 118 | 1482074143 |
| 119 | 1653668665 |
| 120 | 1844349560 |
| 121 | 2056148051 |
| 122 | 2291320912 |
| 123 | 2552338241 |
| 124 | 2841940500 |
| 125 | 3163127352 |
| 126 | 3519222692 |
| 127 | 3913864295 |
| 128 | 4351078600 |
| 129 | 4835271870 |
| 130 | 5371315400 |
| 131 | 5964539504 |
| 132 | 6620830889 |
| 133 | 7346629512 |
| 134 | 8149040695 |
| 135 | 9035836076 |
| 136 | 10015581680 |
| 137 | 11097645016 |
| 138 | 12292341831 |
| 139 | 13610949895 |
| 140 | 15065878135 |
| 141 | 16670689208 |
| 142 | 18440293320 |
| 143 | 20390982757 |
| 144 | 22540654445 |
| 145 | 24908858009 |
| 146 | 27517052599 |
| 147 | 30388671978 |
| 148 | 33549419497 |
| 149 | 37027355200 |
| 150 | 40853235313 |
| 151 | 45060624582 |
| 152 | 49686288421 |
| 153 | 54770336324 |
| 154 | 60356673280 |
| 155 | 66493182097 |
| 156 | 73232243759 |
| 157 | 80630964769 |
| 158 | 88751778802 |
| 159 | 97662728555 |
| 160 | 107438159466 |
| 161 | 118159068427 |
| 162 | 129913904637 |
| 163 | 142798995930 |
| 164 | 156919475295 |
| 165 | 172389800255 |
| 166 | 189334822579 |
| 167 | 207890420102 |
| 168 | 228204732751 |
| 169 | 250438925115 |
| 170 | 274768617130 |
| 171 | 301384802048 |
| 172 | 330495499613 |
| 173 | 362326859895 |
| 174 | 397125074750 |
| 175 | 435157697830 |
| 176 | 476715857290 |
| 177 | 522115831195 |
| 178 | 571701605655 |
| 179 | 625846753120 |
| 180 | 684957390936 |
| 181 | 749474411781 |
| 182 | 819876908323 |
| 183 | 896684817527 |
| 184 | 980462880430 |
| 185 | 1071823774337 |
| 186 | 1171432692373 |
| 187 | 1280011042268 |
| 188 | 1398341745571 |
| 189 | 1527273599625 |
| 190 | 1667727404093 |
| 191 | 1820701100652 |
| 192 | 1987276856363 |
| 193 | 2168627105469 |
| 194 | 2366022741845 |
| 195 | 2580840212973 |
| 196 | 2814570987591 |
| 197 | 3068829878530 |
| 198 | 3345365983698 |
| 199 | 3646072432125 |
| 200 | 3972999029388 |
| 201 | 4328363658647 |
| 202 | 4714566886083 |
| 203 | 5134205287973 |
| 204 | 5590088317495 |
| 205 | 6085253859260 |
| 206 | 6622987708040 |
| 207 | 7206841706490 |
| 208 | 7840656226137 |
| 209 | 8528581302375 |
| 210 | 9275102575355 |
| 211 | 10085065885767 |
| 212 | 10963707205259 |
| 213 | 11916681236278 |
| 214 | 12950095925895 |
| 215 | 14070545699287 |
| 216 | 15285151248481 |
| 217 | 16601598107914 |
| 218 | 18028182516671 |
| 219 | 19573856161145 |
| 220 | 21248279009367 |
| 221 | 23061871173849 |
| 222 | 25025873760111 |
| 223 | 27152408925615 |
| 224 | 29454549941750 |
| 225 | 31946390696157 |
| 226 | 34643126322519 |
| 227 | 37561133582570 |
| 228 | 40718063627362 |
| 229 | 44132934884255 |
| 230 | 47826239745920 |
| 231 | 51820051838712 |
| 232 | 56138148670947 |
| 233 | 60806135438329 |
| 234 | 65851585970275 |
| 235 | 71304185514919 |
| 236 | 77195892663512 |
| 237 | 83561103925871 |
| 238 | 90436839668817 |
| 239 | 97862933703585 |
| 240 | 105882246722733 |
| 241 | 114540884553038 |
| 242 | 123888443077259 |
| 243 | 133978259344888 |
| 244 | 144867692496445 |
| 245 | 156618412527946 |
| 246 | 169296722391554 |
| 247 | 182973889854026 |
| 248 | 197726516681672 |
| 249 | 213636919820625 |
| 250 | 230793554364681 |
| 251 | 249291451168559 |
| 252 | 269232701252579 |
| 253 | 290726957916112 |
| 254 | 313891991306665 |
| 255 | 338854264248680 |
| 256 | 365749566870782 |
| 257 | 394723676655357 |
| 258 | 425933084409356 |
| 259 | 459545750448675 |
| 260 | 495741934760846 |
| 261 | 534715062908609 |
| 262 | 576672674947168 |
| 263 | 621837416509615 |
| 264 | 670448123060170 |
| 265 | 722760953690372 |
| 266 | 779050629562167 |
| 267 | 839611730366814 |
| 268 | 904760108316360 |
| 269 | 974834369944625 |
| 270 | 1050197489931117 |
| 271 | 1131238503938606 |
| 272 | 1218374349844333 |
| 273 | 1312051800816215 |
| 274 | 1412749565173450 |
| 275 | 1520980492851175 |
| 276 | 1637293969337171 |
| 277 | 1762278433057269 |
| 278 | 1896564103591584 |
| 279 | 2040825852575075 |
| 280 | 2195786311682516 |
| 281 | 2362219145337711 |
| 282 | 2540952590045698 |
| 283 | 2732873183547535 |
| 284 | 2938929793929555 |
| 285 | 3160137867148997 |
| 286 | 3397584011986773 |
| 287 | 3652430836071053 |
| 288 | 3925922161489422 |
| 289 | 4219388528587095 |
| 290 | 4534253126900886 |
| 291 | 4872038056472084 |
| 292 | 5234371069753672 |
| 293 | 5622992691950605 |
| 294 | 6039763882095515 |
| 295 | 6486674127079088 |
| 296 | 6965850144195831 |
| 297 | 7479565078510584 |
| 298 | 8030248384943040 |
| 299 | 8620496275465025 |
| 300 | 9253082936723602 |
| 301 | 9930972392403501 |
| 302 | 10657331232548839 |
| 303 | 11435542077822104 |
| 304 | 12269218019229465 |
| 305 | 13162217895057704 |
| 306 | 14118662665280005 |
| 307 | 15142952738857194 |
| 308 | 16239786535829663 |
| 309 | 17414180133147295 |
| 310 | 18671488299600364 |
| 311 | 20017426762576945 |
| 312 | 21458096037352891 |
| 313 | 23000006655487337 |
| 314 | 24650106150830490 |
| 315 | 26415807633566326 |
| 316 | 28305020340996003 |
| 317 | 30326181989842964 |
| 318 | 32488293351466654 |
| 319 | 34800954869440830 |
| 320 | 37274405776748077 |
| 321 | 39919565526999991 |
| 322 | 42748078035954696 |
| 323 | 45772358543578028 |
| 324 | 49005643635237875 |
| 325 | 52462044228828641 |
| 326 | 56156602112874289 |
| 327 | 60105349839666544 |
| 328 | 64325374609114550 |
| 329 | 68834885946073850 |
| 330 | 73653287861850339 |
| 331 | 78801255302666615 |
| 332 | 84300815636225119 |
| 333 | 90175434980549623 |
| 334 | 96450110192202760 |
| 335 | 103151466321735325 |
| 336 | 110307860425292772 |
| 337 | 117949491546113972 |
| 338 | 126108517833796355 |
| 339 | 134819180623301520 |
| 340 | 144117936527873832 |
| 341 | 154043597379576030 |
| 342 | 164637479165761044 |
| 343 | 175943559810422753 |
| 344 | 188008647052292980 |
| 345 | 200882556287683159 |
| 346 | 214618299743286299 |
| 347 | 229272286871217150 |
| 348 | 244904537455382406 |
| 349 | 261578907351144125 |
| 350 | 279363328483702152 |
| 351 | 298330063062758076 |
| 352 | 318555973788329084 |
| 353 | 340122810048577428 |
| 354 | 363117512048110005 |
| 355 | 387632532919029223 |
| 356 | 413766180933342362 |
| 357 | 441622981929358437 |
| 358 | 471314064268398780 |
| 359 | 502957566506000020 |
| 360 | 536679070310691121 |
| 361 | 572612058898037559 |
| 362 | 610898403751884101 |
| 363 | 651688879997206959 |
| 364 | 695143713458946040 |
| 365 | 741433159884081684 |
| 366 | 790738119649411319 |
| 367 | 843250788562528427 |
| 368 | 899175348396088349 |
| 369 | 958728697912338045 |
| 370 | 1022141228367345362 |
| 371 | 1089657644424399782 |
| 372 | 1161537834849962850 |
| 373 | 1238057794119125085 |
| 374 | 1319510599727473500 |
| 375 | 1406207446561484054 |
| 376 | 1498478743590581081 |
| 377 | 1596675274490756791 |
| 378 | 1701169427975813525 |
| 379 | 1812356499739472950 |
| 380 | 1930656072350465812 |
| 381 | 2056513475336633805 |
| 382 | 2190401332423765131 |
| 383 | 2332821198543892336 |
| 384 | 2484305294265418180 |
| 385 | 2645418340688763701 |
| 386 | 2816759503217942792 |
| 387 | 2998964447736452194 |
| 388 | 3192707518433532826 |
| 389 | 3398704041358160275 |
| 390 | 3617712763867604423 |
| 391 | 3850538434667429186 |
| 392 | 4098034535626594791 |
| 393 | 4361106170762284114 |
| 394 | 4640713124699623515 |
| 395 | 4937873096788191655 |
| 396 | 5253665124416975163 |
| 397 | 5589233202595404488 |
| 398 | 5945790114707874597 |
| 399 | 6324621482504294325 |
| 400 | 6727090051741041926 |
| 401 | 7154640222653942321 |
| 402 | 7608802843339879269 |
| 403 | 8091200276484465581 |
| 404 | 8603551759348655060 |
| 405 | 9147679068859117602 |
This question is raised and discussed in my forum at Wizard of Vegas.
As asked in the movie Mean Girls, what is:
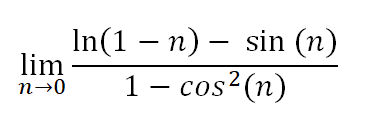
Let's start by looking at a graph of n (x-axis) by f(n) (y-axis).
As you can see, the limit approaches ∞ from the left and -∞ from the right. Since it doesn't converse to the same place from both sides, there is no limit.
However, let's answer the question without graphing. L'Hôpital's rule says that if the limit of f(x)/g(x) = 0/0, then lim f(x)/g(x) = lim f'(x)/g'(x). So, let's solve for f'(x) and g'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos2(n)) d/dn = sin2(n) d/dn
Let's use the product rule to solve for sin2(n) d/dn
sin2(n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n).
Next, let's solve for f'(n) and g'(n) at n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sin(0)cos(0) = 0
So, f'(0)/g'(0) = -2/0 = -∞. Thus, the limit of the original function doesn't exist.

I would like to compliment the writers of Mean Girls for getting the math in this movie perfect. Even serious mathematical movies, like Good Will Hunting, often completely blow the math.
In the season 3 episode 4 of Young Sheldon, titled Hobbitses, Physicses and a Ball With Zip, Sheldon asks himself the number of possible combinations on a bingo card. What is the answer and are the formulas shown on the show correct?
First, I'll go over the number of permutations. This means that not only do the numbers matter but also their order on the card. There are permut(15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360,360 possible permutations for the B, I, G, and O columns. For the N column, the number of permutations is permut(14,4) = 15!/(15-4)! = 15*14*13*12 = 32,760. Thus, the total number of permutations of bingo cards is 360,3604 × 32,760 = 552446474061128648601600000.
Second, I'll go over the number of combinations. This means that the numbers matter but not their order on the card. There are combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3,003 possible combinations for the B, I, G, and O columns. For the N column, the number of permutations is combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1,365. Thus, the total number of permutations of bingo cards is 3,0034 × 1,365 = 111007923832370565.
On the show, Sheldon asks himself how may UNIQUE bingo cards exist. Based on the later incorrect formulas, I assume he means permutations. In other words, two cards with the same numbers but in different positions would both be unique.
The image above shows Sheldon's formula for the B, I, G, and O columns. He initially gets the formula right at 5! × combin(15,5). However, he incorrectly simplifies it to 15!/(15!-5)!. The second exclamation point shouldn't be there. It should read 15!/(15-10)!. However, he then gets back to the correct answer at 360,360.

We have exactly the same problem with the N column. The formula should be 15!/(15-4)!, not 15!/(15!-4)!. The second exclamation point ruins it.
The ironic thing is later in the Episode, Sheldon become obsesses with errors in the chronology of the Lord of the Rings, much as I'm obsessing with this.

There’s a full 100-liter tank containing a water and 10 kg salt. If we add 10 liters pure water per minute, while simultaneously draining 10 liters of the solution per minute, how much salt will be left in the tank after 30 minutes?
Let's start by defining a couple variables:
- s = kg of salt in the tank
- t = minutes since the salt was dumped in the tank
We're given that 10% of the salt is drained away per minute. To put that in mathematical language:
ds/dt = (-10/100) × s
Let rearrange that to:
ds = (-10/100) × s dt
-10/s ds = dt
Integrating both sides:
(1) -10×ln(s) = t + c
Next, let's find the dreaded constant of integration. To do that, we're given that s = 10 when t = 0. Plugging that into formula (1) above gives us:
-10 × ln(10) = 0 + c
So c = -10×ln(10)
Putting that into equation (1) gives us:
(2) -10×ln(s) = t -10×ln(10)
The question at hand is how much salt will be in the tank at t=30. Solving for s when t=30:
-10×ln(s) = 30 -10×ln(10). Next divide both sides by -10...
ln(s) = -3 + ln(10)
s = exp(-3 + ln(10))
s = exp(-3) × exp(ln(10))
s = exp(-3) × 10
s =~ 0.4979 kg of salt.
This question is asked and discussed in my forum at Wizard of Vegas.
Given the larger figure is a square, what is the area of x?
The key to problems like this is in setting them up. I recommend trying to boil the problem down to as few unknowns as possible. In this case, we can express the unknown distances on the square to just three, as follows:
It's easier to deal with rectangles than triangles. Given we know the area of three triangles, we can double the size and double the areas. That gives us:
- ab=10
- ac=16
- (a-b)(a-c)=14
Let's factor (a-b)(a-c):
a2 - ab- ac + bc = 14
a2 - 10 - 16 + bc = 14
(1) a2 + bc = 40
Let's express b and c in terms of a, to get this down to a single variable:
b = 10/a
c = 16/a
Substituting those values for b and c in equation (1):
a2 + (10/a)*(16/a) = 40
a2 + 160/a2 = 18
Next, let's get rid of that a2 in the denominator by multiplying everything by a2.
a4 + 160 = 40*a2
a4 - 40*a2 + 160 = 0
Let's define a new variable y = a2
y2 - 18y + 32 = 0
Next, let's solve for y using the quadratic formula:
y = (40 +/- sqrt(1600-640))/2
y = (40 +/- sqrt(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
The area of the entire square is a2, which conveniently is equal to y. From the equation above, if the +/- is negative, then y = apx 4.5081, which is obviously wrong, since we know the area is at least 20, not even including x. So that area of the square must be 20 + 4*sqrt(15).
The three triangles we're given have an area of 5+7+8=20. Subtracting that from the total area of the square leaves us the area of x: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = apx 15.4919.
This question is raised and discussed in my forum at Wizard of Vegas.

Note my t-shirt in this picture. The movie theater cashier complimented it when I went to see Uncut Gems. I thanked her by torturing her with this problem, only with triangles of areas 2, 3 and 4. After the movie, I checked on her and she still hadn't solved it, but seemed to be trying. So I wrote out the following solution at the Suncoast bar for her. She actually seemed to appreciate it. I think that young woman will go far in life.
There is a square dartboard of dimensions 1 by 1. A dart is thrown at it such that it can land anywhere with equal probability. Let the coordinates of where is lands be (x,y), where both x and y are uniformly and independently distributed from 0 to 1.
Let z = round(x/y). In other words, z = x/y, rounded to the nearest integer. What is the probability that z is even?
It will be very useful to know the infinite series in the following hint.
The Leibniz formula for π states:
1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
For the answer only, click the following button.
Click the button below for the solution.
If x/y < 0.5, then the ratio will round dow n to 0, and even number. Any point on the dartboard on the left of the line formed by (0,0) and (0.5) will round down to 0. That area is a right triangle with side of 1 and 1/2. Remember the area of a triangle is (1/2)*base*height. Thus the area of those points rounding down 0 to is (1/2)*(1/2) = 1/4.
The next area on the graph that will round to the next even number, 2, is when 1.5 < x/y < 2.5. This area will be a triangle with base 2/3 - 2/5 and height 1. Note these are the inverses of the bounds of x/y, because x equals 1, so we need to invert y. So, the area that rounds to 2 is (1/2)*(2/3 - 2/5).
The next area on the graph that will round to the next even number, 4, is when 3.5 < x/y < 4.5. This area will be a triangle with base 2/7 - 2/9 and height 1. So, the area that rounds to 2 is (1/2)*(2/7 - 2/9).
The next area on the graph that will round to the next even number, 6, is when 5.5 < x/y < 6.5. This area will be a triangle with base 2/11 - 2/13 and height 1. So, the area that rounds to 2 is (1/2)*(2/11 - 2/13).
Starting to see a pattern? It goes:
1/4 + 1/2*(2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =
1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
Let's move a -1 inside those parenthesis.
5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ... ) =
5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ... ) =
Next, recall our hint above:
1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11
Getting back to the question at hand ...
5/4 - π/4 =
(5 - π) / 4 = apx. 0.464601836602552.
Interesting how π and e keep popping up all over the place in math.
This question is asked and discussed in my forum at Wizard of Vegas.
Let 9x + 12x = 16x
What is x?
Click the button below for the answer.
Click the button below for the solution.
9x + 12x = 16x =
Divide both sides by 9x
1 + (12/9)x = (16/9)x
1 + (4/3)x = ((4/3)x)2
(1) Let u = (4/3)x
1 + u = u2
By the quadratic formula...
u = (1+sqrt(5)) / 2 (The Golden Ratio)
Putting that back in equation (1):
(4/3)x = (1+sqrt(5)) / 2
Take the log of both sides:
x ln(4/3) = ln[(1+sqrt(5)) / 2]
x = ln[(1+sqrt(5)) / 2] / ln(4/3)
x = [ln(1+sqrt(5) - ln(2)] / [ln(4) - ln(3)] = apx. 1.67272093446233.
This question is raised and discussed in my forum at Wizard of Vegas.
Acknowledgement: I got a variation of this problem from Presh Talwalkar of Mind Your Decisions.
A farmer plants 5 apple seeds. Each day, each seed will have a 1/3 chance of sprouting. What is the average time until all five trees sprout?
A farmer plants 5 apple seeds. Each day, each seed will have a 1/3 chance of sprouting. What is the average time until all five trees sprout?
Let's work out way backwards. If there is one seed left that hasn't sprouted, it will take on average 1/p days to sprout, where p is the probability of sprouting any given day. Since p = 1/3, it will take on average 3 days to sprout. Let's call that t1 = 3.
What if there are two seeds left? There is a p2 = 1/9 chance both will sprout in the next day and we're done. The chance one will sprout the next day is 2×p×q, where q is the chance of not sprouting. Thus, the chance of one seed sprouting is 2×(1/3)(2/3) = 4/9. The chance of neither seed sprouting is q2 = (2/3)2 = 4/9. Let's call the expected number of days with two seeds t2.
t2 = 1 + (4/9)×t1 + (4/9)t2
t2 = (1 - (4/9)) = 1 + (4/9)×t1
t2 = (1 + (4/9)×3) / (1 - (4/9))
t2 = (21/9) / (5/9)
t2 = (21/9) × (9/5) = 21/5 = 4.2
What if there are three seeds left? There is a p3 = 1/27 chance all will sprout in the next day and we're done. The chance one will sprout the next day is 3×p×q2 = 3×(1/3)(2/3)2 = 12/27. The chance two will sprout the next day is 3×p2×q = 3×(1/3)2×(2/3) = 6/27. The chance of no seeds sprouting is q3 = (2/3)3 = 8/27. Let's call the expected number of days with three seeds t3.
t3 = 1 + (6/27)t1 + (12/27)×t2 + (8/27)×t3
t3 = 1 + (6/27)×3 + (12/27)×4.2 + (8/27)×t3
t3 × (1 - 8/27) = (1 + 18/27 + 28/15)
t3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = apx. 5.02105263
What if there are four seeds left? There is a p4 = 1/81 chance all four will sprout in the next day and we're done. The chance one will sprout the next day is 4×p×q3 = 4×(1/3)(2/3)3 = 32/81. The chance two will sprout the next day is combin(4,2)×p2×q2 = 6×(1/3)2×(2/3)2 = 24/81. The chance three will sprout the next day is combin(4,3)×p3×q = 4×(1/3)3×(2/3) = 8/81. The chance of no seeds sprouting is q4 = (2/3)4 = 16/81. Let's call the expected number of days with three seeds t4.
t4 = 1 + (8/81)×t1 + (24/81)×t2 + (32/81)×t3 + (16/81)×t4
t4 = 1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263 + (16/81)×t4
t4 = (1 + (8/81)×3 + (24/81)×4.2 + (32/81)×5.02105263) / (1 - (16/81))
t4 = apx. 5.638056680161943319838056680.
What if there are all five seeds left? There is a p5 = 1/243 chance all 5 will sprout in the next day and we're done. The chance one will sprout the next day is 5×p×q4 = 5×(1/3)(2/3)4 = 80/243. The chance two will sprout the next day is combin(5,2)×p2×q3 = 10×(1/3)2×(2/3)3 = 80/243. The chance three will sprout the next day is combin(5,3)×p3×q = 10×(1/3)3×(2/3)2 = 40/243. The chance four will sprout the next day is combin(5,4)×p4×q = 5×(1/3)4×(2/3) = 10/243. The chance of no seeds sprouting is q5 = (2/3)5 = 32/243. Let's call the expected number of days with three seeds t5.
t5 = 1 + (10/243)×t1 + (40/243)×t2 + (80/81)×t3 + (80/243)×t4 + (32/243)×t5
t5 = (1 + (10/243)×t1 + (40/243)×t2 + (80/81)×t3 + (80/243)×t4) / (1 - (32/243))
t5 = (1 + (10/243)×3 + (40/243)×4.2 + (80/243)×(477/95) + (80/243)×5.63805668) / (1 - (32/243))
t5 = apx. 6.131415853.
This problem is adapted from a similar problem by Presh Talwalkar of Mind Your Decisions.
I have a two-part question.
For part 1, given:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
What is x^4 + y^4 + z^4 ?
For the second part, what is the answer to the general case when:
- x + y + z = a
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
Question 1: 97/6 = apx. 16.166666
Question 2: a4/6 + (4/3)ac - a2b + b2/2
For see my solution (PDF)
This question is raised and discussed in my forum at Wizard of Vegas.
A microbe, let’s call it Covid-20 can spawn a new microbe at any time. The probability of a particular microbe spawning at any given time, from a specific parent microbe, is always the same, regardless of the time since the last spawning. The average time between spawnings from the same microbe is one day. In mathematical terms, the expected time between spawnings from the same microbe follows an exponential distribution with a mean of one day.
Once a microbe enters your lungs, what is the expected number of microbes will you have after seven days?
Click the button below for the answer.
Click the button below for the solution.
This solution will require an ordinary differential equation. If you're not at that point yet in your math education, you won't get it.
Let:
m = Number of Covid-20 microbes
t = time, in days
Since each microbe average a new microbe once per day, m microbes will average m new microbes per day. In other words, the rate of increase in microbes (m) at any given time t can be written as:
dm/dt = m.
I'm not sure the proper way to express this, but separate the dt to the right side:
dm = m dt.
Divide both sides by m:
1/m dm = 1 dt.
Integrate both sides:
ln(m) = t + C, where C is the constant of integration.
We're given that at time 0 there is one microbe. In other words when t = 0, m = 1. We can put those values in the equation above to solve for C:
ln(1) = 0 + C
0 = 0 + C
C = 0.
We now have ln(m) = t.
Take the exp() of both sides:
m = et
So, at time t=7, there will be e7 = apx. 1096.6332 microbes.
This question is asked and discussed in my forum at Wizard of Vegas.
In an old western saloon, an argument over a game of cards escalated into all the cowboys in the vicinity drawing their guns and shooting at each other.
When the smoke finally cleared, 90% of the cowboys had been shot in the leg, 85% had been shot in the arm, 80% had been shot in the gut, and 75% had been shot in the head. Surprisingly, only the cowboys who received all four types of wounds died in the big gunfight.
What is the smallest possible percentage of cowboys who ended up being laid to rest?
First, shoot 90% of the cowboys in the leg.
Next, shoot the 10% left standing in the arm. You have 75% more to shoot in the arm, so take them from those already shot in the leg.
So, now we're at:
Leg only 15% (90% - 75%)
Arm only 10%
Both 75%
Neither 0%
Total leg: 90%
Total arm: 85%
Next, let's go onto the gut injuries (80%). Shoot the 25% with just one injury in the gut. We have 80%-25% = 55% more people to shoot. We will take that 55% from the pool of people with both injuries. So now we're at:
Leg & gut 15%
Arm & gut 10%
Leg & arm 20% (75% - 55%)
All three 55%
One injury 0%
Zero injuries 0%
Finally, consider the 75% with head injuries. First, shoot the 45% with exactly two injuries. We have 30% more to go, so get them from the 55% with all three injuries. That leaves:
Head, Leg & gut 15%
Head, Arm & gut 10%
Head, Leg & arm 20%
Leg, arm & gut: 25% (55% - 30%)
All four 30%
Zero injuries 0%
One injury 0%
Two injuries 0%
Let there be 20 cowboys. We choose this number because all the probabilities involved are evenly divisible by 5% and 5% of 20 is 1.
Line them up in a row. Then, starting with the left, shoot 90% of them, which comes to 18, in the leg. Then make a diagram with the cowboy number along the top row and the total injuries of each along the left column, as follows.
| Injury | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | ||
| 2 | ||||||||||||||||||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| Total | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Next, you'll need to shoot 85%, or 17 in the arm. Start with the two cowboys not shot in the leg. You have 15 more to go. Go back to the cowboy on the left and move down the row, shooting a total of 15 already shot in the leg. Your injury card should look like this:
| Injury | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | A | A |
| 2 | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | |||||
| 3 | ||||||||||||||||||||
| 4 | ||||||||||||||||||||
| Total | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 |
Next, you'll need to shoot 80%, or 16 in the gut. Start with the FIVE cowboys with one injury only. You have 11 more to go. Go back to the cowboy on the left and move down the row, shooting a total of 11 already shot twice. Your injury card should look like this:
| Injury | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | A | A |
| 2 | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | G | G | G | G | G |
| 3 | G | G | G | G | G | G | G | G | G | G | G | |||||||||
| 4 | ||||||||||||||||||||
| Total | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Next, you'll need to shoot 75%, or 15 in the head. Start with the nine cowboys shot twice only. You have 6 more to go. Go back to the cowboy on the left and move down the row, shooting a total of 6 already shot three times. Your injury card should look like this:
| Injury | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | L | A | A |
| 2 | A | A | A | A | A | A | A | A | A | A | A | A | A | A | A | G | G | G | G | G |
| 3 | G | G | G | G | G | G | G | G | G | G | G | H | H | H | H | H | H | H | H | H |
| 4 | H | H | H | H | H | H | ||||||||||||||
| Total | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
As you can see, 6 cowboys have been shot four times and 14 three times. Thus the maximum percentage that can sustain three injuries only is 14/20 = 70%.
For the general case, if the four probabilities are a, b, c, and d, then the maximum ratio that can live is 1-(a+b+c+d), as long as a+b+c+d >=3 and a+b+c+d <=4.
I would like to thank and credit Wizard of Vegas forum member CharliePatrick for this solution.
This question is asked and discussed in my forum, beginning with this post.
A frog can jump one foot or two feet. The frog jumps a total of ten feet exactly over multiple jumps, always forward. How many different ways can this be done, considering both jump distance and order?
- If the frog needs to jump one foot only, there is obviously one way only. Remember, the frog can't overshoot his goal.
- If the frog needs to jump two feet, there are two ways this can be done -- (1) 1 foot and 1 foot, or (2) 2 feet.
If the frog needs to jump three feet, he can be either one foot or two feet away before the final jump. There is one way to be two feet away, as shown from step 1, and two ways to be one foot away, as shown from step 2. Thus, there are three ways to jump three feet away. This is also easily verified as (1) 1+1+1, (2) 1+2, (3) 2+1.
If the frog needs to jump four feet, he can be either two feet or three feet away before the final jump. There are 2 ways to be 2 feet away, as shown from step 2, and 3 ways to be 1 foot away, as shown from step 3. Thus, there are 5 ways to jump four feet away. This is also easily verified as (1) 1+1+1+1, (2) 1+1+2, (3) 1+2+1, (4) 2+1+1, (5) 2+2.
If the frog needs to jump 5 feet, then he can be either 3 feet or 4 feet away before the final jump. There are 3 ways to be 2 feet away, as shown from step 3, and 5 ways to be 1 foot away, as shown from step 4. Thus, there are 3+5=8 ways to jump five feet away. This is also easily verified as (1) 1+1+1+1+1, (2) 1+1+1+2, (3) 1+1+2+1, (4) 1+2+1+1, (5) 2+1+1+1, (6) 2+2+1, (7) 2+1+2, (8) 1+2+2.
Do you start to see a pattern? It is the Fibonacci sequence. Continuing with the same logic, there are 89 ways the frog can jump exactly a total of ten feet.Using the standard U.S. coins of 1, 5, 10, 25, 50 cents and $1, how many ways can one make change for $1?
Let a(x) = number of ways to make x cents, using only pennies and nickles, where x is evening divisible by 5.
a(x) = 1+(x/5)
In other words, the number of ways is the number of possible nickles in the change, which will range from 0 to x/5.
Let b(x) = number of ways to make x cents, using only pennies, nickles, and dimes, where x is evening divisible by 5.
b(0)=1
b(5)=2
b(x) = a(x) + b(x-10), where x>=10.
In simple English, the number of ways to make x cents, is the sum of (1) b(x-10) = number of ways for x-10 cents by adding a dime to each way and (2) a(x) = Number of ways using no dimes.
Let c(x) = number of ways to make x cents, using only pennies, nickles, dimes, and quarters where x is evening divisible by 25.
c(0) = 1
c(x) = b(x) + c(x-25), where x>=25.
In simple English, the number of ways to make x cents, is the sum of (1) c(x-25) = number of ways for x-25 cents by adding a quarter to each way and (2) b(x) = Number of ways using no quarters.
Let d(x) = number of ways to make x cents, using only pennies, nickles, dimes, quarters, and half dollars where x is evening divisible by 50.
d(0) = 1
d(x) = c(x) + d(x-50), where x>=50.
In simple English, the number of ways to make x cents, is the sum of (1) d(x-50) = number of ways for x-50 cents by adding a half dollar to each way and (2) c(x) = Number of ways using no half dollars.
Following is a table showing these values for x = 5 to 100.
Ways to Make Change
| x | a(x) | b(x) | c(x) | d(x) |
|---|---|---|---|---|
| 0 | 1 | 1 | 1 | |
| 5 | 2 | 2 | 0 | |
| 10 | 3 | 4 | 0 | |
| 15 | 4 | 6 | 0 | |
| 20 | 5 | 9 | 0 | |
| 25 | 6 | 12 | 13 | |
| 30 | 7 | 16 | 0 | |
| 35 | 8 | 20 | 0 | |
| 40 | 9 | 25 | 0 | |
| 45 | 10 | 30 | 0 | |
| 50 | 11 | 36 | 49 | 50 |
| 55 | 12 | 42 | 0 | |
| 60 | 13 | 49 | 0 | |
| 65 | 14 | 56 | 0 | |
| 70 | 15 | 64 | 0 | |
| 75 | 16 | 72 | 121 | |
| 80 | 17 | 81 | 0 | |
| 85 | 18 | 90 | 0 | |
| 90 | 19 | 100 | 0 | |
| 95 | 20 | 110 | 0 | |
| 100 | 21 | 121 | 242 | 292 |
Finally, add one for the $1 coin and the answer is 292+1 = 293.
This question is raised and discussed in my forum at Wizard of Vegas.
There are an infinite number of light bulbs, all turned off. The time between light bulbs being turned on has an exponential distribution* with a mean of one day. Once a light bulb is turned on, its life expectancy also follows an exponential distribution with a mean of one day.
What is the mean time until the first light bulb burns out?
*: Random events that follow the exponential distribution have a memory-less property in that the past does not matter. In other words, a single event is never over-due and the probability of it happening is always the same.
On average, it will take one day for the first light bulb to be turned on.
From there, it will take half a day, on average, until the next significant event, either a new bulb being turned on or the first bulb burning out. We add 1/2 a day to the waiting time until that event. So, we're now at 1 + (1/2) = 1.5 days.
There is a 1/2 chance the second event was a second bulb being turned on. In that case, there is a 1/3 day waiting time until the next significant event (either one of the first two bulbs burning out or a new bulb being turned on). So, add the product of 1/2 (the probability of getting this far) and 1/3, which equals 1/6, to the waiting time. So, we're not at 1.5 + 1/6 = 5/3 = 1.66667 days.
There is a (1/2)*(1/3) = 1/6 chance the third signficant event was a third bulb being turned on. In that case, there is a 1/4 day waiting time until the next significant event (either one of the first three bulbs burning out or a new bulb being turned on). So, add the product of 1/6 (the probability of getting this far) and 1/4, which equals 1/24, to the waiting time. So, we're not at 5/3 + 1/24 = 41/24 = 1.7083 days.
Following this pattern, the answer is (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
It should be common knowledge that e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...
The only difference is our answer lacks the 1/0! factor. Thus, the answer is e - 1/0! = e - 1 = apx. 1.7182818...
This question is asked and discussed in my forum at Wizard of Vegas.
A, B, C, and D are all different positive integers.
A < B < C < D
Find the largest D so that
1/A + 1/B + 1/C + 1/D = 1
The answer is 42. A, B, and C are 2, 3, and 7.
1/2 + 1/3 + 1/7 + 1/42 = 1.
This question is asked and discussed in my forum at Wizard of Vegas.
After watching through The Queen's Gambit, I noticed none of the games on the show ended in a draw. I thought chess at high levels had lots of draws. For grandmaster-level chess, what percentage of games end in a draw?
According to the article Has the number of draws in chess increased? at ChessBase.com, author Qiyu Zhou states that in 78,468 rated games between players rated games of 2600 or over (it takes 2500 to be a grandmaster), the following are the results:
- Black wins: 18.0%
- White wins: 28.9%
- Draw: 53.1%
There is a 5x5 pegboard and 3 pegs. What is the probability that three randomly placed pegs form a triangle?
First, there are combin(25,3) = 2,300 possible combinations for the pegs.
How many of those combinations form a triangle? Let’s use this board to help:
First, there are five rows, five columns, and two diagonals. For any one of them there are combin(5,3) = 10 ways to place the pegs in a line. So there are 12*10 = 120 combinations that way.
Second, there are four ways to connect the center square of a row/column to a center square of an adjacent row/column. In other words, these three placements:
- A3, B4, C5
- C5, D4, E3
- E3, D2, C1
- C1, B2, A3
So, now we’re at 120 + 4 = 124
Third, there are four different diagonal lines that are four spaces:
- A2, B3, C4, D5
- B5, C4, D3, E2
- E4, D3, C2, B1
- D1, C2, B3, A4
For each of them there are combin(4,3)=4 ways to place three pegs. So that adds 4*4 = 16 more.
We are now at 124+16 = 140
Fourth, consider the way knights move in chess, in a 2x1 L shape. For each corner there are two ways a knight can move. In all of them the knight may move again in the same line formed the first move. So that is 4*2 = 8 more:
- A1, C2, E3 A1, B3, C5
- A5, B3, C1
- A5, C4, E3
- E5, C4, A3
- E5, D3, C1
- E1, D3, C5
- E1, C2, A3
There are also four such knight lines that go through the center:
- A2, C3, E4
- A4, C3, E2
- B5, C3, D1
- D5, C3, B1
Adding the 12 knight lines, we are at 140+12= 152
If there are 2,300 total combinations and 152 form lines, then 2300-152 = 2,148 don’t form lines and thus form triangles.
Thus, our answer is 2,148/2,300 = 93.39%.
This question is asked and discussed in my forum at Wizard of Vegas.
You are given:
- There is an airplane eight miles directly above a surface to air missile, which is fired at that moment.
- At all times, the airplane travels in a straight direction.
- The airplane travels at 600 miles per hour.
- The missile travels at 2000 miles per hour.
- The missile always travels at an angle that directly faces the airplane.
Questions:
- How far will the plane travel before struck by the missile?
- How long will it take for the missile to strike the plane?
- How long is the flight path of the missile?
- How far will the plane travel before struck by the missile? = 240/91 miles
- How long will it take for the missile to strike the plane? = 2/455 hours
- How long will the missile travel? = 800/91 miles
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
Assume:
- 90% of the public wears masks.
- The probability of getting the coronavirus is 1% for wearers and 3% for non-mask wearers.
Somebody is chosen at random with the coronavirus. What is the probability he is a mask wearer?
This is a classic Bayesian conditional probability question.
The answer is probability(somebody is a mask-wearer and has coronavirus)/probability(somebody has coronavirus) =
(0.9*0.01) / (0.9*0.01 + 0.1*0.03) = 75%.
There is an ant in the middle of a square. He is 17" from the upper-left corner, 20" from the upper-right corner, and 13" from the lower-right corner.
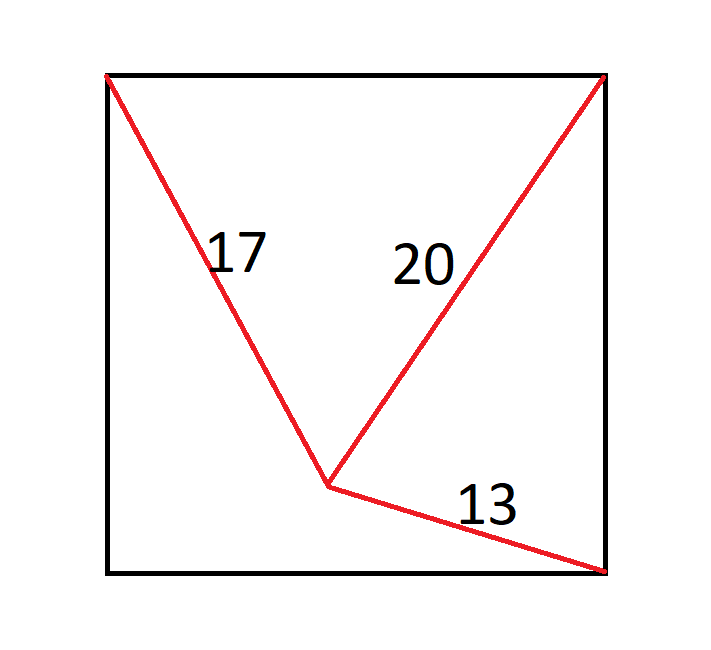
How large is the square?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
First, rotate triangle ABE 90 degrees to form a new triangle BDF.
Since the triangle was rotated 90 degrees, angle EBF=90, by definition. By the Pythagorean formula, EF = 20*sqrt(2).
By the law of cosines: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
Recall, sin^2(x) + cos^2(x) = 1. Let's use that to solve for sin(DEF).
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
Next, consider angle BED.
Angle BED = Angle BEF + Angle FED.
We know EBF is 90 degrees and an isosceles triangle. That would make angle BEF 45 degrees.
So, Angle BED = 45 degrees + Angle FED.
Recall, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Let's apply the law of cosines again, this time to triangle BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD is the side of the square in question, so BD^2 is the area of that square, which we have shown is 369.
This question is asked and discussed in my forum at Wizard of Vegas.
You are a pyrotechnician in charge of the nightly firework display at an amusement park. You've received some new style rockets from Europe and are testing one in order to time it to your show's music soundtrack.
The firework rocket is fired vertically upwards with a constant acceleration of 4 ms^-2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 meters where it detonates.
Assuming no air resistance and taking acceleration due to gravity is 9.8 meters per second per second, how long does it take the rocket to reach its maximum height?
Let:
t = time since rocket fuel runs out.
r = time rocket fuel lasted.
I'm going to express acceleration in terms of an upward direction. So, the acceleration after the rocket fuels burns out is -9.8.
As a reminder, the integral of acceleration is velocity and the integral of velocity is location. Let's make location relative to the ground.
When the rocket is first launched, we're given that the acceleration is 4.
Taking the integral, the velocity of the rocket after r seconds equals 4r.
Taking the integral of the velocity gives us the location of the rocket after r seconds of 2r2.
Now let's look at what happens after the rocket fuel burns out.
We're given that acceleration due to gravity is -9.8.
The velocity due to gravity at time t is -9.8t. However, it also has upward velocity of 4r from the rocket.
Let v(t) = velocity at time t
v(t) = -9.8t + 4r
The rocket will achieve a maximum height when v(t) = 0. Let's solve for that.
v(t) = 0 = -9.8t + 4r
4r = 9.8t
t = 40/98 r = 20r/49.
In other words, whatever time the rocket fuel lasted, the rocket will keep traveling up for 20/49 of that time.
We are also given the distance traveled at the maximum altitude achieved is 138.
Let's take the integral of v(t) to get the formula for distance traveled, which we'll call d(t).
d(t) = -4.9t2 + 4rt + c, were c is a constant of integration.
As we already showed, the rocket traveled 2r2 by the time the fuel burned out, so that must be the constant of integration. That gives us:
d(t) = -4.9t2 + 4rt + 2r2
We know the maximum altitude of 138 was reached at time 20r/49 So let's plug t=20r/49 into the equation to solve for r:
d((20r/49) = -4.9((20r/49)2 + 4r(20r/49) + 2r2 = 138
r2*(-1960/2401 + 80/49 + 2) = 138
r2 = 49
r = 7
So, the rocket fuel lasted for seven seconds.
We already know the rocket kept going up for 20/49 of that time, which is 140/49 = apx. 2.8571 seconds.
Thus, the time from launch to maximum velocity is 7 + 140/49 = 483/49 = apx. 9.8571 seconds
This question is asked and discussed in my forum at Wizard of Vegas.
What is the expected number of rolls of two dice to achieve every total from 2 to 12? Please use calculus for your solution.
Recall the probability of rolling a total of 2 is 1/36. In t rolls the expected rolls with a total of 2 is t/36. Assume the time between rolls is distributed exponentially with a mean of t/36. The Poisson distribution tells us the probability of zero rolls with a total of 2 is exp(-t/36).
Recall the probability of rolling a total of 3 is 2/36 = 1/18. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 3 is exp(-t/18).
Recall the probability of rolling a total of 4 is 3/36 = 1/12. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 4 is exp(-t/12).
Recall the probability of rolling a total of 5 is 4/36 = 1/9. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 5 is exp(-t/9).
Recall the probability of rolling a total of 6 is 5/36. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 6 is exp(-5t/36).
Recall the probability of rolling a total of 7 is 6/36 = 1/6. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 7 is exp(-t/6).
The probabilities for 8 to 12 are the same as for 2 to 6.
Thus, the probability that in t units of every total has been rolled at least once is:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
The probability at least total has NOT been rolled in t units of time is 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
To get the expected time without at least one total we integrate the function above from 0 to infinity.
An integral calculator (I recommend this one) will easily solve this as 769767316159/12574325400 = apx. 61.2173847639572 rolls.
This question is asked and discussed in my forum at Wizard of Vegas.
A cuboid is a three-dimensional block, composed of unit-squares.
An a × b × c cuboid is constructed out of abc identical unit cubes, like a 3x3x3 Rubik's Cube. Divide the cubes into two mutually exclusive types. External cubes are those that constitute the faces of the cuboid; internal cubes are completely enclosed. For example, the cuboid pictured has 74 external and 10 internal cubes.
Give the dimensions of all cuboids such that the number of external cubes equals the number of internal cubes.
- 5 X 13 X 132
- 5 X 14 X 72
- 5 X 15 X 52
- 5 X 16 X 42
- 5 X 17 X 36
- 5 X 18 X 32
- 5 X 20 X 27
- 5 X 22 X 24
- 6 X 9 X 56
- 6 X 10 X 32
- 6 X 11 X 24
- 6 X 12 X 20
- 6 X 14 X 16
- 7 X 7 X 100
- 7 X 8 X 30
- 7 X 9 X 20
- 7 X 10 X 16
- 8 X 8 X 18
- 8 X 9 X 14
- 8 X 10 X 12
This question is asked and discussed in my forum at Wizard of Vegas.
Let 0 < a < b. Which is more a^b or b^a?
The answer depends on a and b specifically, but two rules of thumb will address most situations.
If a > e, then a^b > b^a
If b < e, then a^b < b^a
If a < e and b > e, then there is not enough information to determine.
Here is the solution (PDF).
A grenade is thrown down a bottomless pit. On average, the grenade explodes in six seconds. The time until it explodes has a memoryless property, in that the probability of an explosion at any given moment is always the same and independent of low long it has been since the pin was pulled. In other words, it’s lifetime follows the exponential distribution. Assume acceleration of 32 feet per second.
Here is my full solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
Consider a game show with two contestants who are both selfish and perfect logicians. Here are the rules.
- The host places $1,000,000 on a table between the two contestants.
- Contestant A is asked to make a suggestion on how to divide the money between the two contestants.
- Contestant B will be asked to accept or reject the suggestion.
- If contestant B accepts the suggestion, then they divide the money that way and the game is over.
- If contestant B rejects the suggestion, then the host will remove 10% of the amount currently on the table.
- The host will then ask contestant B to make a suggestion and contestant A will have the same chance to accept or reject it.
- If contestant A accepts the suggestion, they split it that way and the game is over. If he rejects it, then the host rakes another 10% of the remaining amount on the table. Then go back to step 2 and keep repeating until a suggestion is accepted.
The question is how should contestant A suggest dividing the money on his initial turn?
He should suggest keeping 10/19 of the money for himself, less one penny, and offer B 9/19 of the money, plus a penny. In other words:
A: $526,315.78
B: $473,684.22
The key is A should put B as close as possible to an indifference point.
Let's call the ratio of the pot to the other player r. If B accepts the offer, he gets r×$1,000,000.
If B rejects the offer, then the host rakes out 10%. After which, B will have a position advantage and would offer contestant A a share of r and keep 1-r for himself.
Solving for r...
r×$1,000,000 = (1-r)×$900,000.
r×$1,900,000 = $900,000.
r = $900,000/$1,900,000 = 9/19.
A does not want B to be completely indifferent, lest a chose randomly and stand a chance of the host raking the pot. So, A should throw in the extra penny to B and offer him (9/19) × $1,000,000 + $0.01 = $473,684.22.
A: $526,315.78
B: $473,684.22
This question is asked and discussed in my forum at Wizard of Vegas.
Two cities, Fauntleroy and Southworth, lay directly across a channel. Two ferries go back and forth all day long between the two cities. The ferries travel at different speeds. At the same time, they both start out, one from each city.
The first time they cross is 5 miles from Southworth. The second time they cross is 3 miles from Fauntleroy. Assume no time to load and unload, but both make an immediate u-turn. Also assume they go in a straight line.
How far apart are the two cities?
Let t2 = time until second crossing
r = ratio of speed of ferry initially leaving Fauntleroy to the speed of the ferry initially leaving Southworth.
c = Distance of channel between two cities.
We are given that the first time they cross is 5 miles from Southworth. To express this in formulas:
c-5 = r*t1
5 = t1
Equating t1, we get:
c-5 = 5r, or r = (c-5)/5
We are also given that second time they cross is 3 miles from Fauntleroy. To express this in formulas:
3c - 3 = r*t2
c+3 = t2
Equating t2, we get:
2c - 3 = r*(c+3)
Substitute r=(c-5)/5
2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c^2 - 2c - 15
c^2 - 12c = 0
c - 12 = 0
c = 12
So, the channel is 12 miles long.
In the following diagram, what is the area of the blue region?
Click the button below for the answer.
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
In a chess tournament, each contestant plays a match against every other contestant. Each contestant gets 1 point for every match he wins, 0.5 points for every tied match, and 0 for every game he loses.
At the end of the tournament, it is seen that all competitors got a different number of points and the last competitor in the score ranking defeated each of the top three competitors.
Accordingly, what is the minimum number of competitors participating in the tournament?
Let's call the number of players n.
I figure the last place player has only three wins, against the top 3 players, and lost every other game. That gives him 3 points.
I then figure every subsequent player in order of points as 0.5 more points than the previous one, in rank. That would give the highest ranking player 3+(n-1)/2 points.
Taking the sum of 3 to 3+(n-1)/2, by a 1/2 point per step gives us (((n+5)*(n+6)/2)-15)/2.
The total games played with n players is n*(n-1)/2, where everybody players everybody else, once. Each game results in one total point, to that is also the total points earned among all players.
Then solve for n:
(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n-2
n=13
The following table shows a way this can happen. The body of the table shows the winner in all 78 games.
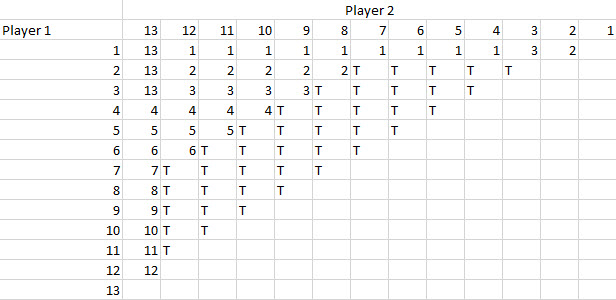
The following table shows the number of points of each player.
Total Points by Player
| Player | Points |
|---|---|
| 13 | 3 |
| 12 | 3.5 |
| 11 | 4 |
| 10 | 4.5 |
| 9 | 5 |
| 8 | 5.5 |
| 7 | 6 |
| 6 | 6.5 |
| 5 | 7 |
| 4 | 7.5 |
| 3 | 8 |
| 2 | 8.5 |
| 1 | 9 |
This question is asked and discussed in my forum at Wizard of Vegas.
Which is the more efficient way to stack cannonballs, in a pyramid with a square base, like the pyramids of Egypt, or triangular, forming a tetrahedron?


Here are a couple formulas the reader may find helpful:
Scroll down for my answer and solution.
By "efficient," I shall assume you mean which has the least wasted space between cannonballs.
To keep things simple, to define the volume of either pyramid, let's use the center of the balls located at the corners of the pyramid. Let's let n be the number of cannonballs in a side of the base of either pyramid.
Let's look at the pyramid with square base first.
The number of cannonballs in the whole pyramid is 12 + 22 + 32 + 42 + 52 + 62 + ... + n2 = n*(n+1)*(2n+1)/6.
Next, let's find the height of this square pyramid where a side of the base is n. As can be seen in the picture, the sides (other than the square base) are equilateral triangles. Thus, the slant height is also n. The distance from one corner of the base to the opposite corner is n*sqrt(2). The distance from a corner of the base to the center of the base is thus n*sqrt(2)/2. Let the height be h. Consider the right triangle formed by the height, distance from a corner of the base to the center of the base, and the slant height.
h2 + (n*sqrt(2)/2)2 = n2
h = n*sqrt(2)/2.
Recall the volume of a pyramid is base*height/3. That makes the volumne of the pyramid:
n2 * n* sqrt(2)/2 * (1/3) = n3*sqrt(2)/6.The ratio of balls to volume is thus [n*(n+1)*(2n+1)/6] / [n3*sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2*n3) = sqrt(2)*(n+1)*(2n+1)/(2*n2)
Next, let's look at the pyramid with a triangular base.
The number of cannonballs in the whole pyramid is 1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6.
Next, let's find the area of the base. Recall, the sides of a 30-60-90 triangle are proportional to 1/2, sqrt(3)/2, and 1. From that, it is not difficult to find the height of an equalateral trinagle of side n is n*sqrt(3)/2. This makes the area of the base n2*sqrt(3)/4.
The distance from a corner of the base to the center of the base is sqrt(3)/3. Given that and the slant height of 1 of the pyramid, we can use Pythagorean to find the height of the pyramid as sqrt(6)/3.
We can now find the volume of the pyramid as base*height/3 = (n2*sqrt(3)/4) * (n*sqrt(6)/3) * (1/3) = n3*sqrt(18)/36 = n3*sqrt(2)/12.
The ratio of balls to volume is thus [n*(n+1)*(n+2)/6] / [n3*sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2*n3) = sqrt(2)*(n+1)*(n+2)/n2
Here is a comparison of the balls to volume ratios:
- Square base: sqrt(2)*(n+1)*(2n+1)/(2*n2)
- Triangle base: sqrt(2)*(n+1)*(n+2)/n2
Let's divide both ratios by sqrt(2)*(n+1)/n2:
- Square base: (2n+1)/2 = n + 0.5
- Triangle base: n+2
As n gets larger, the ratio of balls to volume will approach n for both pyramids. In other words, the large numbers of cannonballs, the more they are equally efficient.
Given the volume of a cannonball, the efficiency in both pyramids, defined as the ratio of cannonball volume to total volume, approaches pi*sqrt(2)/6 =~ apx. 74.05%.
This question is asked and discussed in my forum at Wizard of Vegas.
For any given large number, what is the average distance between primes near that number? Also, how many primes are there less than that number?
A very good estimate for the average distance between primes near any large number n is ln(n). It is remarkable how how good this estimator is.
As evidence, the following table shows the range of the first 15 million primes, in groups of one million. The table shows the average distance in the range between primes and the estimate of the average distance. The estimate is the natural log of the average of the largest and smallest prime in the range. For example, for the 15th group of a million primes, it is ln((256,203,221+275,604,541)/2).
Average Distance Between Primes
| First Prime in Range |
Last Prime in Range |
Primes in Range |
Average Distance | Estimate | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1,000,000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1,000,000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1,000,000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1,000,000 | 19.40132 | 19.39864545 |
Source: The Gaps Between Primes at Prime Pages.
To get the number of primes under any given number, we can start by integrating the average distance estimate of ln(n). This will give us the sum of average distances between primes up to any number n.
What is the integral of f(n)=ln(n)? Recall that integration by parts tells us:
Integral of f(n)*g'(n) dn = f(n)*g(n) - integral of (f'(n)*g(n)) dn
Let f(n)=ln(n) and g'(n)=1. Then f'(n)=1/n and g(n)=n. The integral of ln(n) will thus be ln(n)*n - integral of ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
If we divide n*(ln(n)-1) by n, we get the average distance between primes for the range of numbers from 2 to n. This is ln(n)-1.
If we divide n by this average distance between primes, we get the average number of primes under n, which equals n/(ln(n)-1).
As evidence, the following table shows the number of primes under various large numbers and the estimated value. Please excuse the 15 significant digits of precision, which is all Excel will allow. Somebody, please, make a spreadsheet that can handle more.
Average Distance Between Primes
| n | Primes under n | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 100,000,000 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
Source: How Many Primes are There? at Prime Pages.
The figure above is a nonagon with side length one.
Which is more, AB+AC or AE?
This problem was taken from the March 2021 issue of the Mensa Bulletin.
Here is my solution to this problem. (PDF)
How can I easily find the square root of any three- or four-digit number, assuming the answer is an integer?
The following table shows the numbers 0 to 9, the square of each and the last digit of that square.
Last Digit of Square Numbers
| Original Number |
Square | Last digit of Square |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Note that numbers are even squares always end in 0, 1, 4, 5, 6, or 9. This is true for all squares. This is because the last digit of the original number determines the last digit of the square.
Step 1: Based on the last digit of the square, we can use the following table to narrow down the last digit of the square root. For example, if 2809 is the square, then the last digit of the square root is 3 or 7.
Last Digit of Original Number
| Last digit of Square Root |
Last digit of Square |
|---|---|
| 0 | 0 |
| 1 | 1 or 9 |
| 4 | 2 or 8 |
| 5 | 5 |
| 6 | 4 or 6 |
| 9 | 3 or 7 |
Step 2: Next, take the original number and drop the right two digits. For example, if the original number were 2809, then use 28.
Step 3: Find the smallest square number less than or equal to the result of step 2. Then, take the square root of that square number. For example, the smallest square less then 28 is 25. Take the square root of 25 and you get 5.
If you haven't memorized the squares up to 100, then you may use the following table.
First Portion of Square Root
| Step 2 | Step 3 |
|---|---|
| 1 to 3 | 1 |
| 4 to 8 | 2 |
| 9 to 15 | 3 |
| 16 to 24 | 4 |
| 25 to 35 | 5 |
| 36 to 48 | 6 |
| 49 to 63 | 7 |
| 64 to 80 | 8 |
| 81 to 99 | 9 |
Step 4: If the result from step 1 is a 0 or 5, then put that after the result from step 3 and you're done.
Otherwise, let a = result from step 3. Let b=a×(a+1). For example, if the result from step 3 where 5, then b=5×6=30.
Step 5: If b < a, then the final digit of the square root is the lesser of the possibilities from step 1. Otherwise, if b >= a, then it is the greater of the two possibilities.
Step 6: To get the square root, take the result from step 3 and then follow it with the result from step 5. In other words 10×(step 3)+step 5.
Let's look at some examples:
Find the square root of 256.
- Step 1: The last digit of the square root is 4 or 6.
- Step 2: Dropping the last two digits, we get 2.
- Step 3: The smallest square less than or equal to 2 is 1. The square root of 1 is 1.
- Step 4: 1*(1+1) = 2.
- Step 5: The result from step 4 is equal to that of step 2, so we use the larger of the options from step 1 as the last digit, which is 6.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 1 & 6 = 16.
Find the square root of 1369.
- Step 1: The last digit of the square root is 3 or 7.
- Step 2: Dropping the last two digits, we get 13.
- Step 3: The smallest square less than or equal to 13 is 9. The square root of 9 is 3.
- Step 4: 3*(1+3) = 12.
- Step 5: The result from step 2 is greater than that of step 4, so we use the larger of the options from step 1 as the last digit, which is 7.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 3 & 7 = 37.
Find the square root of 2704.
- Step 1: The last digit of the square root is 2 or 8.
- Step 2: Dropping the last two digits, we get 27.
- Step 3: The smallest square less than or equal to 27 is 25. The square root of 25 is 5.
- Step 4: 5*(1+5) = 60.
- Step 5: The result from step 2 is less than that of step 4, so we use the smaller of the options from step 1 as the last digit, which is 2.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 5 & 2 = 52.
Find the square root of 5625.
- Step 1: The last digit of the square root is 5.
- Step 2: Dropping the last two digits, we get 56.
- Step 3: The smallest square less than or equal to 56 is 49. The square root of 49 is 7.
- Step 4: The result from step 1 is a 0 or 5, so the answer is the result from step 3 appended by that of step 1: 7 & 5 = 75
Find the square root of 6561.
- Step 1: The last digit is 1 or 9.
- Step 2: Dropping the last two digits, we get 65.
- Step 3: The smallest square less than or equal to 65 is 64. The square root of 64 is 8.
- Step 4: 8*(1+8) = 72.
- Step 5: The result from step 2 is less than that of step 4, so we use the lesser of the options from step 1 as the last digit, which is 1.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 8 & 1 = 81.
You may see a demonstration of this method on YouTube.
What is the area of a regular pentagon with side length 1?
Click the box below for the answer.
Click the box below for a hint.
Consider the image above. AC = CD.
Here is my solution (PDF)
On a windless day, Charlie takes his canoe to the river and paddles up upstream. He always paddles at the same rate (in other words if we ignore the current, he would always go the same speed). A mile after launching, his hat falls in the river. Ten minutes after that, he realizes his hat is missing and immediately makes a u-turn to catch up to it downstream. Charlie catches up to his hat at the same place he launched.
How fast is the current?
Click the button below for the answer.
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
The following question refers to a bar bet. A random U.S. serial number for any bill is used. The player selects any three digits from 0 to 9. He must select three different numbers. Wins are based on how many of these three selected digits appear at least once on the serial number.
For example, if the player selections 7-0-2 and the serial number is 22227755, then there are two matches. It does not matter that the 2 and 7 matched multiple times.
Here are the odds offered:
- 3 matches: 5 to 1
- 2 matches: 1 to 1
- 1 match: 9 to 5
- 0 matches: 15 to 1
What is the probability of winning and house edge of each bet?
The following table shows the number of winning combinations, probability of winning, and house edge for each bet. The right column shows the house edge ranges from 7.4% to 8.5%.
Serial Number Bets
| Matches | Pays | Combinations | Probability | House Edge |
|---|---|---|---|---|
| 3 | 5 | 15,426,684 | 0.154267 | 0.074399 |
| 2 | 1 | 45,771,270 | 0.457713 | 0.084575 |
| 1 | 1.8 | 33,037,245 | 0.330372 | 0.074957 |
| 0 | 15 | 5,764,801 | 0.057648 | 0.077632 |
Using each digit from 1 to 9 exactly once each, compose three fractions, each with one digit in the numerator and two digits in the denominator, in which the sum of the three fractions is one.
For example, 8/16 + 9/27 + 3/24 meets every condition, except the sum equals 23/24, not 1.
There are permut(9,3)*permut(6,3)*permut(3,3)/fact(3) = 60,480 possible permutations to sort through to find the answer. I must admit I tried for at least an hour by trial and error and didn't find a solution.
So, I wrote a program to sort through all fact(9) = 362,880 ways to sort the nine digits and tested all of them. The tricky part was to sort through every possible way to order the nine numbers. Here is how to do it, using lexographic sorting.
- Put all nine elements in an array, arranged from lowest to highest.
- Find the last element in the array such that the following element is greater. If none are found, exit the program.
- Starting with the element after that from step 2, find the last element in the array that is greater than that from step 2.
- Swap the elements in the array from steps 2 and 3.
- Reverse the elements in the array from the one after that from step 2 until the end.
- Go back to step 2
Following this process, you'll find the correct answer six times, once for all six ways to order the three fractions.
I wrote the following code, to sort every digit from 1 to 9 in lexographic order and test each one if it was a solution.
void three_fraction(void)
{
int i, x_max, y_max, temp_array[100], hold, pt;
int lex_array[] = { 1,2,3,4,5,6,7,8,9 };
int num_elements = sizeof(lex_array) / sizeof(lex_array[0]);
int count = 0;
bool stop = false;
double tot3;
cerr << "Number of elements =\t" << num_elements << "\n";
do
{
count++;
tot3 = (double)lex_array[0] / (double)(10 * lex_array[1] + lex_array[2]);
tot3 += (double)lex_array[3] / (double)(10 * lex_array[4] + lex_array[5]);
tot3 += (double)lex_array[6] / (double)(10 * lex_array[7] + lex_array[8]);
if (tot3 == 1.0)
{
cerr << count << "\t";
cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
}
x_max = -1;
for (i = 0; i < (num_elements - 1); i++)
{
if (lex_array[i] < lex_array[i + 1])
x_max = i;
}
if (x_max >= 0)
{
y_max = 0;
for (i = x_max + 1; i < num_elements; i++)
{
if (lex_array[x_max] < lex_array[i])
y_max = i;
}
hold = lex_array[x_max];
lex_array[x_max] = lex_array[y_max];
lex_array[y_max] = hold;
if (x_max + 1 < num_elements - 1) // reverse
{
for (i = x_max + 1; i < num_elements; i++)
{
temp_array[i] = lex_array[i];
}
pt = 0;
for (i = x_max + 1; i < num_elements; i++)
{
lex_array[i] = temp_array[num_elements - 1 - pt];
pt++;
}
}
}
else
stop = true;
} while (stop == false);
}
This question is asked and discussed in my forum at Wizard of Vegas.
A man had a 10-gallon keg of wine and a jug. One day, he drew a jug-full of wine and then topped off the keg with water. Later on, when the wine and water had gotten thoroughly mixed, he drew another jug-full and again topped off the keg with water. The keg then contained equal quantities of wine and water.
What was the capacity of the jug?
Let j = volume of jug.
After the first time the jug was filled, there was 10-j gallons of wine left in the jug. After water replaced the wine, the ratio of wine to the entire keg was (10-j)/10.
After the jug scooped out the diluted wine, there was 10-j gallons of diluted wine left in the keg. The amount of pure wine in the diluted wine can be expressed as:
(10-j)*((10-j)/10) = 5
(10-j)^2 = 50
j^2 - 20j + 100 = 50
j^2 - 20j + 50 = 0
j = (20 +/- sqrt(400-200))/2
j = (20 +/- 10*sqrt(2))/2
j = 10 +/- 5*sqrt(2)
The jug can't be bigger than the keg, so we must use the negative sign:
j = 10 - 5*sqrt(2) =~ apx. 2.92893218813452 gallons.
This question is asked and discussed in my forum at Wizard of Vegas.
To celebrate Thanksgiving, you and 19 mathematicians are seated at a circular table. Everyone at the table would like a helping of cranberry sauce, which happens to be in front of you at the moment.
First, you serve yourself. Then, instead of passing the sauce around in a circle, you decide to pass it randomly to the person seated directly to your left or to your right. They then do the same, passing it randomly either to the person to their left or right. This continues until everyone has, at some point, received the cranberry sauce.
Of the 20 people in the circle, who has the greatest chance of being the last to receive the cranberry sauce?
Let's name one of the mathematicians G. In order for G to be last, two things must occur:
- The cranberries must first reach either neighbor of G.
- The cranberries must move 19 positions in the opposite direction without ever reaching G.
To be last, the cranberries must eventually reach either neighbor. So the probability of that is 100%.
Then, whatever the probability is for the second part is, it is the same for each person. Thus, each person has an equal probability of being last.
If that explanation wasn't clear. Gialmere got this problem from fivethirtyeight.com. Here they explain the solution. Scroll down to the part that says "Solution to last week’s Riddler Classic."
This question is asked and discussed in my forum at Wizard of Vegas.
Here is another puzzle from The Riddler.
There are 100 marbles in a bag. Each marble is either red, blue, or green. If three marbles were drawn from the bag, the probability would be 20% of getting one of each color. How many of each color marble are in the bag. Please note I specifically didn't say whether the marbles are drawn with or without replacement.
Let's try to work it out under a "with replacement" assumption. Let r, b, and g be the number of red, blue and green marbles, respectively. Then, the probability of drawing one of each color would be 6*(r/100)*(b/100)*(g/100). Setting that equal to 0.2, we can say:
6*(r/100)*(b/100)*(g/100) = 0.2
6*r*b*g = 200000
6 does not divide into 200,000 evenly. Thus, there are no integer solutions possible for r*b*g = 33333.333... So, we can eliminate the case of drawing with replacement
Next, let's try the "without replacement" assumption. In this case, the probability of drawing one of each color is r*b*g/combin(100,3) = 0.2. Trying to solve for that...
r*b*g/161700 = 0.2
r*b*g = 32340
The prime factorization of 32340 is 2*2*3*5*7*7*11.
We need to distribute those factors between r, b, and g, while maining r+b+g=100. For example, we could try:
r = 2*3*5 = 30
b = 2*11 = 22
g = 7*7 = 49
While these correctly use up all the prime factors, r+b+g = 101, so it's not a valid solution.
I'm afraid I had to write a brute force looping program to get an the solution of r, b, and g having values of 21, 35, and 44, in any order.
The following question comes to us courtesy of the Riddler Express.
Let's assume NFL rules. Consider the following situation:
- The Red team is down 14 points late in the game
- The Red team will have two more possessions
- The Blue team will have zero more possessions
- Let's ignore field goals and safeties, as the Red team must score two touchdowns to have a chance at winning
- If the game goes into overtime, each team will have a 50% chance to win. The game cannot end in a tie.
- The probability of making a one-point kick after a touchdown is 100%.
- The probability of making a two-point conversion is p.
At what value of p should the red team be indifferent to kicking and going for a two-point conversion after a first touchdown (now down by 8)?
Let p = indifference point between going for the two-point conversion and the kick.
If the first two-point conversion attempt is successful, then the red team can kick the ball the second time and win.
If the first two-point conversion attempt is unsuccessful, then the red team must try again after the second touchdown and then win the game in overtime.
The probability of winning, going for the two-point conversion after the first touchdown is p + (1-p)*p/2. We equate this to the 50% chance of winning by kicking after the first touchdown and solve for p.
p + (1-p)*p/2 = 1/2
2p + (1-p)*p = 1
3p - p^2 = 1
p^2 - 3p + 1 = 0
Using the quadratic formula, solve for p:
p = (3 +/- sqrt(5))/2
We take the negative option, to keep p between 0 and 1, to get p = (3-sqrt(2))/2 = apx. 0.381966011250105
This question is asked and discussed in my forum at Wizard of Vegas.
In the previous Ask the Wizard column, you were asked about the expected number of rolls to achieve a total of 12 with two dice twice in a row. On a related note, I see somebody on your forum is claiming to have witnessed 18 consecutive yo's (total of 11) at the craps table. What is the expected rolls required for that to happen?
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
The exact answer found with the aid of WizCalc.
A grassy field is in the shape of a circle of radius 100m and is enclosed by a circular fence. A goat is attached by a chain to a hook, at a fixed point on the fence. To stop the goat getting too fat, the farmer wants to make sure that it can only reach half of the grass in the field. How long should the chain be?
By way of illustration, the circle represents the grassy field. The S represents where the chain is staked on the edge of the field. The yellow portion of the circle is where the goat can reach. The green area is beyond the reach of the chain. The goal is to make the chain the right distance so the green and yellow portions are equal.
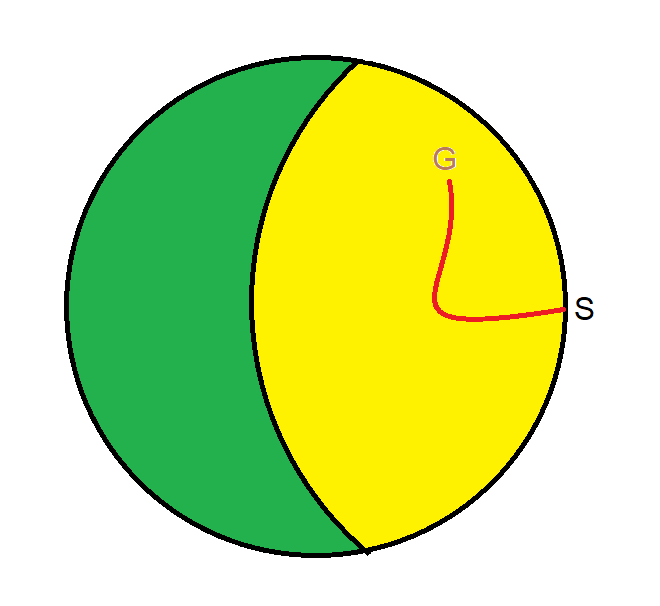
Please refer to the following diagram in solving this problem.
The point Q is the center of the grassy circle. The goat's chain is staked to point R. The goat can reach all the colored regions, including their mirror image below the line PR.
You're given that the radius of the grassy circle is 100, so b+c = d = 100.
The way I'm going to solve this is to define everything in terms of b. Then I'll play around with b until I achieve the desired result where the goat can eat half the grass.
Let's start by solving for e in term of b. Looking at triangle with sides b, d, and e and using the Pythagorean formula:
b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = sqrt(10000 - b^2)
Next, let's solf for f in terms of b. Remember, we already know b+c=100, so c=100-b. Using Pythagoras:
c^2 + e^2 = f^2
(100-b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)
Next, let's find the area of triangle QRS:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
Next, let's find the area of the slice of the grassy as cut out by the angle SQR:
tan(SQR) = e/b = sqrt(10000-b^2)/b.
slice SQR = atan(sqrt(10000-b^2)/b)
The red area equals the slice SQR minus traingle QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).
Next, let's find the blue + green + yellow + purple area. To do this, we need to find the angle QRS.
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
angle QRS = atan(sqrt(10000-b^2)/(100-b)).
Add to that the red area and we have half the total area the goat can eat:
atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).
Double that, for the part below line PR to get the total area:
2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).
The total area of the grassy region is 10,000*pi.
Now, just play around with b until you get an area the goat can eat equal to 5,000*pi. The goalseek function in Excel is great for problems like this. How anyone accomplished anything before spreadsheets, I have no idea.
Using this method, you will find that b = 32.867402.
From there we can get f = length of the chain = 115.8728598 meters.
This question is asked and discussed in my forum at Wizard of Vegas.
What is your recommended starting word in Wordle?
To answer that, I first looked at the frequency of each letter in each position, based on the list of allowed Wordle solutions.
Letter Frequency in Wordle
| Letter | Pos. 1 | Pos. 2 | Pos. 3 | Pos. 4 | Pos. 5 | Total |
|---|---|---|---|---|---|---|
| A | 141 | 304 | 307 | 163 | 64 | 979 |
| B | 173 | 16 | 57 | 24 | 11 | 281 |
| C | 198 | 40 | 56 | 152 | 31 | 477 |
| D | 111 | 20 | 75 | 69 | 118 | 393 |
| E | 72 | 242 | 177 | 318 | 424 | 1233 |
| F | 136 | 8 | 25 | 35 | 26 | 230 |
| G | 115 | 12 | 67 | 76 | 41 | 311 |
| H | 69 | 144 | 9 | 28 | 139 | 389 |
| I | 34 | 202 | 266 | 158 | 11 | 671 |
| J | 20 | 2 | 3 | 2 | 0 | 27 |
| K | 20 | 10 | 12 | 55 | 113 | 210 |
| L | 88 | 201 | 112 | 162 | 156 | 719 |
| M | 107 | 38 | 61 | 68 | 42 | 316 |
| N | 37 | 87 | 139 | 182 | 130 | 575 |
| O | 41 | 279 | 244 | 132 | 58 | 754 |
| P | 142 | 61 | 58 | 50 | 56 | 367 |
| Q | 23 | 5 | 1 | 0 | 0 | 29 |
| R | 105 | 267 | 163 | 152 | 212 | 899 |
| S | 366 | 16 | 80 | 171 | 36 | 669 |
| T | 149 | 77 | 111 | 139 | 253 | 729 |
| U | 33 | 186 | 165 | 82 | 1 | 467 |
| V | 43 | 15 | 49 | 46 | 0 | 153 |
| W | 83 | 44 | 26 | 25 | 17 | 195 |
| X | 0 | 14 | 12 | 3 | 8 | 37 |
| Y | 6 | 23 | 29 | 3 | 364 | 425 |
| Z | 3 | 2 | 11 | 20 | 4 | 40 |
Then I looked at all the words in the Wordle solution list with five distinct letters and scored them according to the letter frequency table above. I awarded two points for a match in the correct position and one point for a match in an incorrect position. Then I sorted the list, which you see below.
Best Starting Words in Wordle
| Rank | Word | Points |
|---|---|---|
| 1 | Stare | 5835 |
| 2 | Arose | 5781 |
| 3 | Slate | 5766 |
| 4 | Raise | 5721 |
| 5 | Arise | 5720 |
| 6 | Saner | 5694 |
| 7 | Snare | 5691 |
| 8 | Irate | 5682 |
| 9 | Stale | 5665 |
| 10 | Crate | 5652 |
| 11 | Trace | 5616 |
| 12 | Later | 5592 |
| 13 | Share | 5562 |
| 14 | Store | 5547 |
| 15 | Scare | 5546 |
| 16 | Alter | 5542 |
| 17 | Crane | 5541 |
| 18 | Alert | 5483 |
| 19 | Teary | 5479 |
| 20 | Saute | 5475 |
| 21 | Cater | 5460 |
| 22 | Spare | 5457 |
| 23 | Alone | 5452 |
| 24 | Trade | 5449 |
| 25 | Snore | 5403 |
| 26 | Grate | 5403 |
| 27 | Shale | 5392 |
| 28 | Least | 5390 |
| 29 | Stole | 5377 |
| 30 | Scale | 5376 |
| 31 | React | 5376 |
| 32 | Blare | 5368 |
| 33 | Parse | 5351 |
| 34 | Glare | 5340 |
| 35 | Atone | 5338 |
| 36 | Learn | 5324 |
| 37 | Early | 5320 |
| 38 | Leant | 5307 |
| 39 | Paler | 5285 |
| 40 | Flare | 5280 |
| 41 | Aisle | 5280 |
| 42 | Shore | 5274 |
| 43 | Steal | 5268 |
| 44 | Trice | 5267 |
| 45 | Score | 5258 |
| 46 | Clear | 5258 |
| 47 | Crone | 5253 |
| 48 | Stone | 5253 |
| 49 | Heart | 5252 |
| 50 | Loser | 5251 |
| 51 | Taper | 5248 |
| 52 | Hater | 5243 |
| 53 | Relay | 5241 |
| 54 | Plate | 5240 |
| 55 | Adore | 5239 |
| 56 | Sauce | 5236 |
| 57 | Safer | 5235 |
| 58 | Alien | 5233 |
| 59 | Caste | 5232 |
| 60 | Shear | 5231 |
| 61 | Baler | 5230 |
| 62 | Siren | 5226 |
| 63 | Canoe | 5215 |
| 64 | Shire | 5213 |
| 65 | Renal | 5210 |
| 66 | Layer | 5206 |
| 67 | Tamer | 5200 |
| 68 | Large | 5196 |
| 69 | Pearl | 5196 |
| 70 | Route | 5194 |
| 71 | Brace | 5192 |
| 72 | Slice | 5178 |
| 73 | Stage | 5171 |
| 74 | Prose | 5170 |
| 75 | Spore | 5169 |
| 76 | Rouse | 5166 |
| 77 | Grace | 5164 |
| 78 | Solar | 5152 |
| 79 | Suite | 5150 |
| 80 | Roast | 5145 |
| 81 | Lager | 5130 |
| 82 | Plane | 5129 |
| 83 | Cleat | 5129 |
| 84 | Dealt | 5128 |
| 85 | Spear | 5126 |
| 86 | Great | 5126 |
| 87 | Aider | 5123 |
| 88 | Trope | 5116 |
| 89 | Spire | 5108 |
| 90 | Tread | 5107 |
| 91 | Slave | 5097 |
| 92 | Close | 5090 |
| 93 | Lance | 5090 |
| 94 | Rinse | 5088 |
| 95 | Cause | 5087 |
| 96 | Prone | 5087 |
| 97 | Drone | 5082 |
| 98 | Noise | 5079 |
| 99 | Crest | 5073 |
| 100 | Sober | 5068 |
So, there you have it, my recommended starting word, which I use, is STARE.
What is i^i
You wish to play a game that requires two ordinary six-sided dice. Unfortunately, you lost the dice. However, you have nine index cards, which you may mark any way you like. The player must choose two index cards randomly from the nine, without replacement, and take the sum of the two cards.
Mark the cards as follows:
1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5
This question is asked and discussed in my forum at Wizard of Vegas.
Is it true the flip of a fair coin is more likely to land face-up on the side that started face up?
The evidence suggests this is true!
Persi Diaconis and Susan Holmes of Stanford University recorded 10,000 coin flips. The coin landed on the same side face-up as it started 50.8% of the time (source: The Fifty-one Percent Solution from the newsletter What’s Happening in the Mathematical Sciences by the American Mathematical Society). The probability of a ratio that high or more is 5.48%.
To prove this mathematically, I assumed the actual number of revolutions of a coin followed the Poisson distribution. To be more specific, if the mean number of revolutions was m, then the probability of exactly n revolutions is exp(-m)*m^n/n!. To illustrate the Poisson distribution, the following graph shows the probability of 0 to 25 revolutions, given a mean of 10.
The reasons I chose the Poisson assumption is it follows a near bell curve shape for sufficiently large means and the actual result can never go below zero.
I then calculated the probability of an even number of half-revolutions (resulting in the same side landing face up as the starting position) for various means of half revolutions. The following table shows the results for 0.5 to 5.0 means.
Probability Even and Odd Number of Revolutions
| Mean Revolutions | Even Total | Odd Total |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
I then got to wondering why the probability of an even number was always greater than 50%. It turns out the probability of an even number, given a mean of m, can be expressed as 0.5 + e^(-2m)/2. e to the power of anything must be positive, thus the probability of an even number of revolutions is also positive.
You can see my proof of this formula here.
Solve for x:
9x + 12x = 16x
Here is my solution (PDF).
This problem was asked and discussed in my forum at Wizard of Odds.
This problem was inspired by the video A Difficult Exponential Question.
Your office of 100 workers does a Secret Santa gift exchange. This where you write down everybody's name on individual pieces of paper, put them all in a hat, and everybody draws a name at random to give a gift to.
The question is, how many closed loops will there be, on average?
Example of a closed loop of size 4: Gordon gives to Don, Don gives to Jon, Jon who gives to Nathan, and Nathan gives to Gordon.
Drawing your own name would be a closed loop of size 1.
Suppose there is just one employee who comes to the Secret Santa party. Obviously he will pick himself, so one closed loop.
Then a second employee arrives late and asks to join. They give her a list of the now two employees. There is a 1/2 chance she picks employee 1 and 1/2 herself. If she picks employee 1, then she can be squeezed into his loop, where she buys for employee 1 and he buys for her. So, now we're at 1 + 0.5*1 = 1.5
Then a third employee arrives late and asks to join. They give her a list of the now 3 employees. There is a 2/3 chance she picks employee 1 or 2 and 1/3 herself. If she picks employee 1 or 2, then she can be squeezed into their loop, where she buys for employee she picks and the one who formally was supposed to buy for that employee now buys for 3. So, now we're at 1.5 + (1/3) = 11/6.
Then a fourth employee arrives late and asks to join. They give her a list of the now 4 employees. There is a 3/4 chance she picks employee 1 to 3 and 1/4 herself. If she picks employee 1 to 3, then she can be squeezed into their loop, where she buys for employee she picks and the one who formally was supposed to buy for that employee now buys for 4. So, now we're at 11/6 + (1/4) = 25/12.
Keep doing this and the final answer is 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518.
This question is asked and discussed in my forum at Wizard of Vegas.
Consider a semicircle, of radius 1, with two stacked rectangles inside. What is the maximum combined area of the two rectangles?
Here is my full solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
Please ignore identical twins and assume every child has a 50/50 chance of being a born a boy or girl. If children are randomly polled from family sizes of a specified size of 2 to 5, what is the probability a boy or girl will have a sister?
Interestingly, the probability is the same for either gender, regardless of family size.
Let's look at family sizes of three, for example. Here are the eight possible ways to arrange boys and girls, with regard to order:
BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG
If you pick any girl at random from the list above, you'll see that of the 12 girls, 9 have sisters. It is the same for the 12 boys, 9 have sisters. So, the probability is 9/12 = 3/4.
The general formula for the probability of any child having a sister, where the number of children is n, is 1-(1/2)n-1.
Here is the probability of having a sister by total number of children in the family:
- 1: 0
- 2: 1/2
- 3: 3/4
- 4: 7/8
- 5: 15/16
- 6: 31/32
Alternatively, it makes sense the probability would be the same for boys and girls. The gender of your siblings is not correlated to your gender. Thus, only family size matters, not your own gender.
This question is asked and discussed in my forum at Wizard of Vegas.
In episode 4 of season 37 of Survivor, there was a challenge in which four puzzles pieces could be arranged into both a square and an equilateral triangle. What would be the exact dimensions of the pieces for this to work?

|

|
First, let's make a proper diagram and label it.
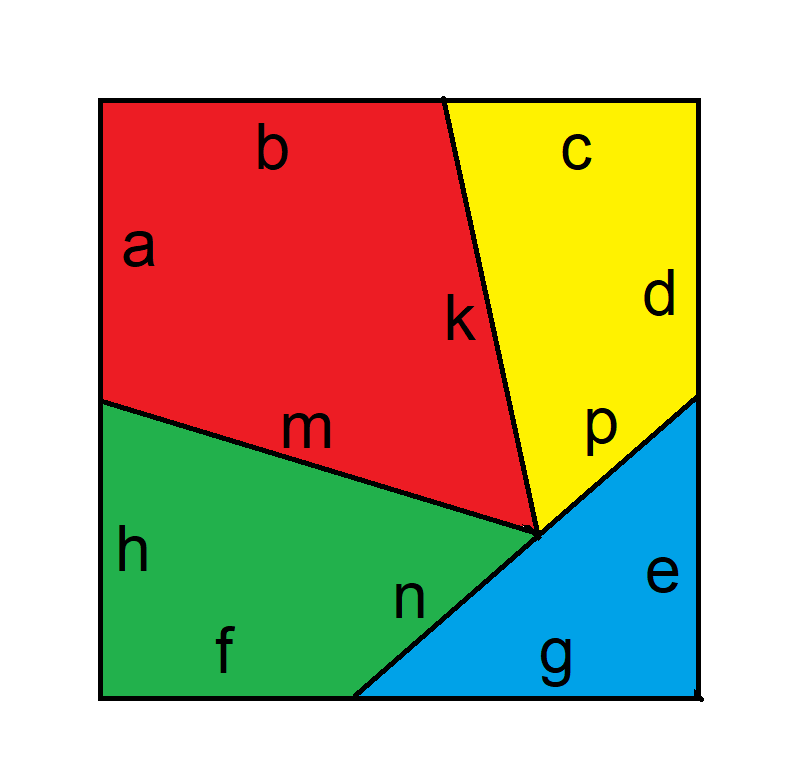
Following is just the diagram of the solved triangle.
Next, assuming the sides of the square are length 1, here is just the length of each letter in the diagram above.
a = d = e = h = 1/2
b = g = SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.572145321740575
c = f = 1-SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0.427854678259425
k = m = 1/SQRT(SQRT(3)) =~ 0.759835685651592
n = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0.386767938902275
p = (SQRT(4*SQRT(3)-3)-1)/(2*SQRT(SQRT(3))) =~ 0.373067746749317
Finally, here is my full solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
I am sure you're a fan of the Big Bang Theory. One of my favorite scenes is the game of Rock Paper Scissors Lizard Spock. It is like a five-symbol game of Rock Paper Scissors, with the following rules:
- Paper covers rock
- Rock crushes lizard
- Lizard poisons Spock
- Spock smashes scissors
- Scissors cuts paper
- Lizard eats paper Spock vaporizes rock
- Scissors decapitates lizard
- Paper disproves Spock
- Rock crushes scissors
My question is can more symbols be added, such that every side has the same chances against a random player?
Yes, I love that scene too! Here is a YouTube video of it.
You need an odd number of symbols. In theory, you could have an even number, but then you would have to make rules where certain pairs of different symbols resulted in a tie. No, we want a decisive game where the only ties are if both players play the same symbol.
A solution is especially elegant and easy to explain with a prime number of symbols. Allow me to explain with seven symbols, as an example. Let's label the symbols A to G and represent them on a circle, in the following diagram.
Next, start with A and then draw an arrow to the next symbol going clockwise. The arrow shall point towards that loses between these two. Think of it like that symbol being shot with an arrow. Keep going clockwise until you get back to A. The diagram will not look like this:
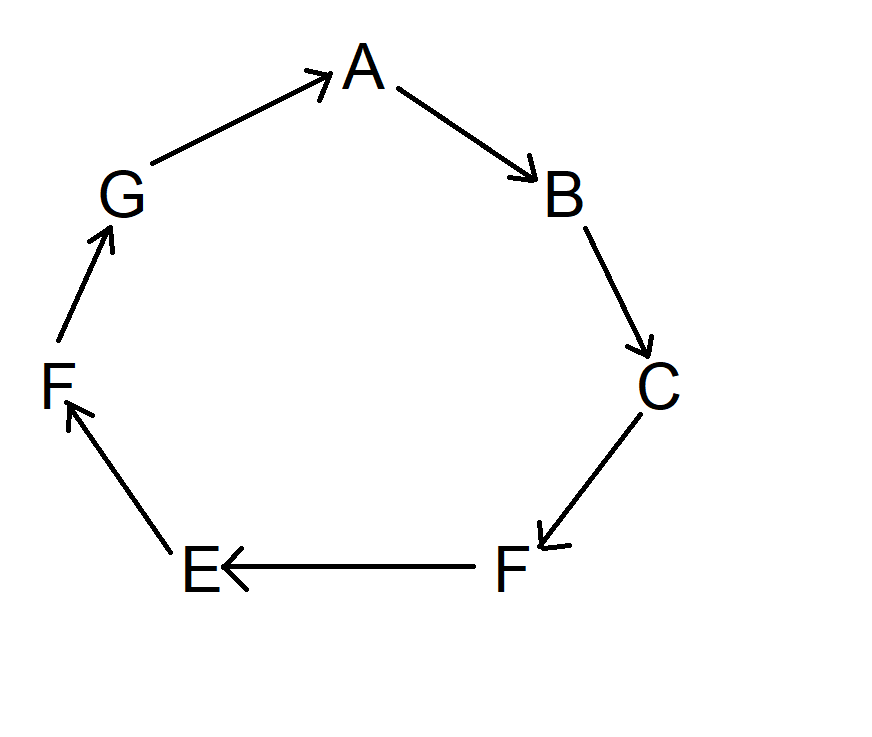
Next, do the same thing, but go two symbols clockwise, starting at A. Actually, you can start anywhere you wish. The diagram now looks like this:
Finally, do the same thing, but skip three symbols clockwise. The diagram now looks like this:
Note at this point every symbol beats three other symbols and is beaten by three other different symbols.
This method will work for any prime number of symbols because by the time you circle back to the original symbol you will have passed through every symbol. For n symbols, you'll have to go through this process (n-1)/2 times.
You can make a balanced game with any odd number of symbols, but you'll loop back to the original symbol too quickly sometimes. When that happens, you'll have to make other loops starting at the symbols you missed.
This question is asked and discussed in my forum at Wizard of Vegas.
You shuffle a standard (28 tile) set of dominos and draw one at random. You carefully uncover one of the sides to reveal a 6. What is the probability that this is the double 6 tile?
For the benefit of those not familiar with dominoes, a domino has two sides, each with a number from 0 to 6. A set consists of one of each possible domino. That would be all combin(7,2)=21 ways to choose numbers, without replacement, out of 7, plus all 7 ways to have both numbers on the same side.
Here are all all 28 of them: 0-0, 0-1, 0-2, 0-3, 0-4, 0-5, 0-6, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-2-2, 2-3, 2-4, 2-5, 2-6, 3-3, 3-4, 3-5, 3-6, 4-4, 4-5, 4-6, 5-5, 5-6, 6-6.
With that explanation out of the way, here are the answer and solution.
A simple way to reword the question is what is the probability a randomly chosen domino has the same number on both sides. That answer is simply 7/28 = 1/4.
You might say, the answer should be 1/7, because the other side could be any of the seven possible numbers. It's true it could be any of the seven numbers, but they are not all equally likely. The 6-6 domino should be double counted, because it has two sides with a six. So, the other side could be either of two sixes and there are eight total sixes in the set. Thus the answer is 2/8 = 1/4.
This question is asked and discussed in my forum at Wizard of Vegas. The question is dedicated to the memory of Alan Mendelson.
Alan and Bob decide to play a tennis until one of them wins two games in a row. The probability of Alan winning any given game is 2/3. What is the probability Alan wins the tournament?
Alan and Bob decide to play a tennis until one of them wins two games in a row. The probability of Alan winning any given game is 2/3. What is the probability Alan wins the tournament?
The following is the generation solution for any probability of Alan winning an individual game.
Let p = probability a wins.
Let a = probability Alan wins tournament after Alan wins last game.
Let b = probability Alan wins tournament after Bob wins last game.
(1) a = p + (1-p)*b
(2) b = p*a
Substituting equation (2) into equation (1):
a = p + (1-p)*pa
a = p + pa - p2*a
a - pa + p2*a = p
a(1-p+p2) = p
(3) a = p/(1-p+p2)
Substituting equation (3) into equation (2):
b = p2/(1-p+p2)
The first game will determine whether the probability of a winning the tournament is a or b:
answer = pa + (1-p)b
= p2/(1-p+p2) + (1-p)*p2/(1-p+p2)
= (2a2-a3)/(a2-a+1)
Plugging a=2/3, gives a probability of winning the tournament of 16/21.
This question is asked and discussed in my forum at Wizard of Vegas.
You have a 5' ladder. You wish to lean it against a wall as high as possible. However, there is a 1x1x1 cubic foot box you must put the ladder over. No, you can't move the box. What is the maximum height the top of the ladder can reach?
Here is my solution (PDF).
At what value is x1/x a maximum?
The answer is e =~ 2.71828182845905.
There, the value of e^(1/e) =~ 1.44466786100977.
Here is my solution (PDF).
Newspapers in 1944 noticed this incredible coincidence:
Is this a big coincidence or is there some mathematical gimmick involved?
It's a mathematical gimmick and the basis of a known magic trick.
For everyone alive in 1944, the sum of their age (after their birthday) and their year of birth was 1944. Think about it. If you were x years old then you were born in 1944-x. The sum is x + (1944-x) = 1944.
It's the same thing the "years in office" in 1944. If you were in office y years, then you must have started in 1944-y. y + (1944-y) = 1944.
The sum of 1944 + 1944 = 3,888. Works every time.
To turn this into a magic trick that works in 2023, as a subject to take the sum of the following four things:
- Year of their birth
- How old will they turn this year.
- Year some significant event happened (like birth of first child).
- Anniversary of that significant event this year.
It will always sum to 2023 + 2023 = 4046.
This question is asked and discussed in my forum at Wizard of Vegas.