On this page
Oscar's Grind Betting System
Introduction
Oscar's Grind is a popular betting system. It is generally played on even money bets with a specified winning goal. Like most betting system, it usually achieves this goal, but at the expense of a large loss when it doesn't. Like every betting system, it can not pass the test of time and will eventually show a net loss.
Unlike most betting systems, like the Martingale, Labouchere or Fibonacci, the player will press his bets after winning, as opposed to losing. It also does not escalate the bet size as fast as these other systems, making it more of a "grind" to achieve the winning goal. This causes the chances of reaching the winning goal to be less than more aggressive systems, but also allows the player to play longer and at a smaller average bet.
Overall, Oscar's Grind will tend to win in a streaky game and do badly in a choppy game.
Rules
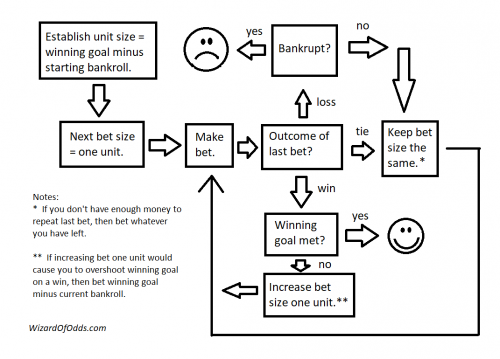
The following is how to play Oscar's Grind on even money bets.
- The player will choose a winning goal and bankroll.
- A one-unit bet shall be equal to the winning goal.
- The player makes a one-unit bet.
- If the player loses or ties, then he repeats the same bet*.
- If the player wins, then he increases he next bet by one unit**.
- The player keeps repeating until he either reaches his winning goal or blows his entire bankroll.
Footnotes:
*: If the player doesn't have enough money to repeat the same bet, then he bets as much he can.
**: If winning the next bet would cause the player to overshoot his winning goal, then he reduces his bet to his winning goal minus his current balance.
Here is my flowchart of how to play. Start in the upper left square. Click on image for larger version.
Simulation Results
To show what to expect from using Oscar's Grind, I wrote a simulation that followed the rules above, based on various bets and games. The simulation used a Mersenne Twister random number generator. For each simulation, the winning goal was ten units. I tested the simulation on the following bankrolls: 10, 25, 50, 100, 250, and 500 units.
The first simulation is based on betting the Player bet in baccarat. The simulation size is over 37 billion sessions. As a reminder, the theoretical house edge on the Player bet is 1.235%.
Baccarat Simulation — Player Bet
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.17% | 95.65% | 97.69% | 98.77% | 99.46% |
| Average number of bets | 4.736 | 5.697 | 6.230 | 6.646 | 7.067 |
| Average units bet | 6.626 | 10.609 | 14.557 | 19.609 | 28.650 |
| Expected win per session | -0.082 | -0.131 | -0.180 | -0.242 | -0.354 |
| Ratio money lost to Money bet | 1.234% | 1.235% | 1.236% | 1.235% | 1.235% |
The first simulation is based on betting the pass bet in craps. The simulation size is over 45 billion sessions. As a reminder, the theoretical house edge on the pass bet is 1.41%.
Craps Simulation — Pass Bet
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.14% | 95.63% | 97.67% | 98.76% | 99.45% |
| Average number of bets | 4.289 | 5.161 | 5.645 | 6.024 | 6.409 |
| Average units bet | 6.001 | 9.616 | 13.205 | 17.804 | 26.051 |
| Expected win per session | -0.085 | -0.136 | -0.187 | -0.252 | -0.368 |
| Ratio money lost to Money bet | 1.413% | 1.414% | 1.414% | 1.414% | 1.413% |
The next simulation is based on the don't pass bet in craps. The simulation size was over 43 billion sessions. As a reminder, the house edge on the don't pass bet is 1.364%.
Craps Simulation — Don't Pass
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 90.14% | 95.64% | 97.68% | 98.76% | 99.46% |
| Average number of bets | 4.410 | 5.307 | 5.805 | 6.193 | 6.589 |
| Average units bet | 6.171 | 9.887 | 13.574 | 18.296 | 26.768 |
| Expected win per session | -0.084 | -0.135 | -0.185 | -0.250 | -0.365 |
| Ratio money lost to Money bet | 1.364% | 1.364% | 1.364% | 1.364% | 1.364% |
The next simulation is based on any even money bet in single-zero roulette. The simulation size was over 43 billion sessions. As a reminder, the theoretical house edge is 1/37 = 2.703%.
Roulette Simulation — Single Zero
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 89.40% | 95.11% | 97.29% | 98.49% | 99.28% |
| Average number of bets | 4.381 | 5.327 | 5.871 | 6.314 | 6.789 |
| Average units bet | 6.156 | 10.059 | 14.074 | 19.418 | 29.545 |
| Expected win per session | -0.166 | -0.272 | -0.380 | -0.525 | -0.799 |
| Ratio money lost to Money bet | 2.703% | 2.702% | 2.703% | 2.702% | 2.703% |
The next simulation is based on any even money bet in double-zero roulette. The simulation size was over 45 billion sessions. As a reminder, the theoretical house edge is 2/38 = 5.263%.
Roulette Simulation — Double Zero
| Statistic | 10 Units | 25 Units | 50 Units | 100 Units | 250 Units |
|---|---|---|---|---|---|
| Probability winning goal reached | 87.81% | 93.93% | 96.39% | 97.81% | 98.81% |
| Average number of bets | 4.567 | 5.670 | 6.350 | 6.944 | 7.646 |
| Average units bet | 6.468 | 10.982 | 15.945 | 23.026 | 37.824 |
| Expected win per session | -0.340 | -0.578 | -0.839 | -1.212 | -1.991 |
| Ratio money lost to Money bet | 5.263% | 5.264% | 5.262% | 5.264% | 5.264% |
Video
Here is my video on Oscar's Grind.
Internal Links
- Labouchere betting system.
- Fibonacci betting system.
- Martingale betting system.
- Anti-Martingale betting system.
- D'Alembert betting system.
- Keefer roulette system.
External Links
Discussion about Oscar's Grind in my forum at Wizard of Vegas.