On this page
Fire Bet
Introduction
The Fire Bet is a popular side bet in craps that pays based on the number of unique points established and won by the shooter. I am aware of three pay tables, as follows. The house edge of each is in the bottom row of the table. Pay Table 1 is the most common. Pays are indicated on a "to one" basis. A negative one indicates a loss.
Fire Bet Pay Tables
| Points Made | Pay Table A | Pay Table B | Pay Table C |
|---|---|---|---|
| 6 | 999 | 2000 | 299 |
| 5 | 249 | 200 | 149 |
| 4 | 24 | 10 | 29 |
| 3 | -1 | -1 | 6 |
| 2 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 0 | -1 | -1 | -1 |
| House edge | 20.76% | 24.86% | 20.73% |
Following is my analysis of Pay Table A. The lower right cell shows a house edge of 20.76%.
Fire Bet — Pay Table A
| Points Made | Pays | Probability | Return |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 24 | 0.008798 | 0.211156 |
| 5 | 249 | 0.001640 | 0.408343 |
| 6 | 999 | 0.000162 | 0.162272 |
| Total | 1 | -0.207628 |
Following is my analysis of Pay Table B. The lower right cell shows a house edge of 24.86%.
Fire Bet — Pay Table B
| Points Made | Pays | Probability | Return |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 10 | 0.008798 | 0.087982 |
| 5 | 200 | 0.001640 | 0.327987 |
| 6 | 2000 | 0.000162 | 0.324869 |
| Total | 1 | -0.248562 |
Following is my analysis of Pay Table C. The lower right cell shows a house edge of 20.73%.
Fire Bet — Pay Table C
| Points Made | Pays | Probability | Return |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | 6 | 0.033434 | 0.200605 |
| 4 | 29 | 0.008798 | 0.255147 |
| 5 | 149 | 0.001640 | 0.244350 |
| 6 | 299 | 0.000162 | 0.048568 |
| Total | 1 | -0.207295 |
The following table shows the probabilities of making 0 to 6 points, with as many significant digits as Excel can handle.
Fire Bet Probabilities
| Points Made | Probability |
|---|---|
| 0 | 0.593939393939394 |
| 1 | 0.260750492003903 |
| 2 | 0.101275355549231 |
| 3 | 0.0334342121788456 |
| 4 | 0.00879817844040312 |
| 5 | 0.00163993313895325 |
| 6 | 0.000162434749269826 |
I often get asked how to calculate the above probabilities. It makes for a challenging math problem. Below, I list there ways to solve for the odds of making any number of points from 0 to 6.
Random Simulation
A random simulation is the easiest way to analyze the Fire Bet. With the speed of modern computers, it is also extremely accurate. Only the most mathematical purists (like me) will strive for an exact solution. The following table shows results of a simulation of almost 40 billion Fire bets resolved against pay table A. The lower right cell shows a house edge of 20.7531%. The actual house edge is 20.7628%, so the simulation was accurate to 0.01% of return.
Fire Bet Simulation
| Points Made | Pays | Wins | Probability | Return |
|---|---|---|---|---|
| 6 | 999 | 6,452,452 | 0.000162 | 0.162257 |
| 5 | 249 | 65,165,019 | 0.001640 | 0.408438 |
| 4 | 24 | 349,553,690 | 0.008799 | 0.211173 |
| 3 | -1 | 1,328,267,592 | 0.033435 | -0.033435 |
| 2 | -1 | 4,023,371,732 | 0.101275 | -0.101275 |
| 1 | -1 | 10,358,742,102 | 0.260747 | -0.260747 |
| 0 | -1 | 23,595,605,529 | 0.593941 | -0.593941 |
| Total | 39,727,158,116 | 1.000000 | -0.207531 |
Markov Chain
A way to calculate the odds of the Fire Bet exactly is with a Markov Chain. This means to calculate the probability of completing any future number of points given any of the 64 possible states of points already completed. The math is fairly easy towards the end, needing only one more point to complete all six. Then work your way back to the beginning state of the first roll.
This first state is represented as the first row in the table, not counting the column headings. It shows the probabilities shown above for completing any number of points from 0 to 6.
Fire Bet Markov Chain
| Points Already Made |
Probability 0 Points |
Probability 1 Points |
Probability 2 Points |
Probability 3 Points |
Probability 4 Points |
Probability 5 Points |
Probability 6 Points |
|---|---|---|---|---|---|---|---|
| None | 0.593939 | 0.260750 | 0.101275 | 0.033434 | 0.008798 | 0.001640 | 0.000162 |
| 10 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 9 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 9,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 8 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 8,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 8,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 6,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 6,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6,8 | 0.000000 | 0.000000 | 0.732710 | 0.210728 | 0.048135 | 0.007762 | 0.000665 |
| 6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 5,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 5,9 | 0.000000 | 0.000000 | 0.685315 | 0.237358 | 0.064328 | 0.011875 | 0.001124 |
| 5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 5,8 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.876957 | 0.114977 | 0.008066 |
| 5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 4,10 | 0.000000 | 0.000000 | 0.647934 | 0.250930 | 0.079930 | 0.018752 | 0.002454 |
| 4,9 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,8 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 4,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.816667 | 0.164832 | 0.018502 |
| 4,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,5,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,5,9 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 4,5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.758221 | 0.208531 | 0.033248 |
| 4,5,8 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4,5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
If you plan to try to recreate my work, here is some advice on going from one state to another. Start with the states close to the end, in which the shooter already made 5 points. For example, if the shooter needs a 4 only, then three things can happen: (1) He establishes and makes the 4, (2) He establishes and makes a point he already made, (3) He sevens out. The probability of (1) is (3/24)*(1/3) = 1/24 = 0.041667. The probability of (2) is (4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0.364394. The probability of (3) is 1- 0.041667 - 0.364394 = 0.593939. Eventually event (1) or (3) will happen. The probability that (1) will happen before (3) is 0.041667/(0.041667+0.593939) = 0.065554.. Recursively work your way back to the starting point. This will either be time-consuming, redundant, and boring, or you can do it in a spreadsheet in an automated manner.
Calculus
The first step in this method is to calculate the probability of all 7 possible pertinent outcomes of a pass line bet after a point is established. We can ignore the 12 combinations, or 1/3 chance, of the player winning or losing immediately on the come out roll, because those events are not significant to the Fire Bet. So the first roll is based on 24 possible combinations, as opposed to 36.
- Point of 4 made and won = (3/24) × (3/9) = 1/24 = apx. 4.17%
- Point of 5 made and won = (4/24) × (4/10) = 1/15 = apx. 6.67%
- Point of 6 made and won = (5/24) × (5/11) = 25/264 = apx. 9.47%
- Point of 8 made and won = (5/24) × (5/11) = 25/264 = apx. 9.47%
- Point of 9 made and won = (4/24) × (4/10) = 1/15 = apx. 6.67%
- Point of 10 made and won = (3/24) × (3/9) = 1/24 = apx. 4.17%
- Any point made and 7-out = 2×((3/24) × (6/9))+ 2× ((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = apx. 59.39%
Please note, the sum of these probabilities equals 1.
Next, instead of the Fire Bet being decided by the roll of two dice, one roll at a time, consider the time between events to occur randomly, with the time between events following an exponential distribution with a mean of one unit of time between events. If an event does occur, the particular event will follow the craps probabilities we just calculated.
For example, the probability of a point-4 win is 1/24. Thus, the time between point-4 wins will average 24 units. The probability of going x units of time without a point-10 win is exp(-x/24). To take the compliment, the probability of at least one point-10 win in x units of time is 1-exp(-x/24).
To adjudicate the Fire Bet, it doesn't matter how much time elapses between events -- just what the events are. So we can the integrate over all time for a winner to the bet as follows:
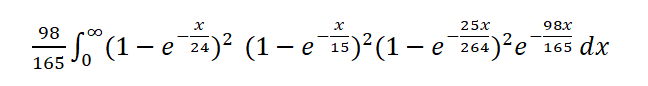
Let me explain what that integral means. It is the probability that after x units of time there has been at least one win of every point but not a 7. Since the probability of a point-4 and point-10 win is the same, we can square the probability of a point-4 win. Same as for 5 and 9, as well as 6 and 8. Finally we multiply the whole thing by 98/165, the probability of a seven-out, to close off the bet. If we didn't do that, the player might get paid for multiple overlapping wins.
Integrating this by hand would be very tedious and error prone. Fortunately, there are integral calculators. To use the one for this problem, click on the link and put the following into the text box at the top: (1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98). Then click on options and set the lower bound to 0 and the upper bound to infinity. Then click go.
Before considering the bounds of integration, the answer is (98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11*e^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(997*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x)/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264))/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^(-(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264))/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165.
Fortunately, that calculator does allow for bounds of integration and gives the solution as 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452, which is approximately equal to 0.0001624347492698264.
Of course, that is just the probability of making all six points, but the same logic could be used to find the probability of any number of points. I'll leave that as an exercise to the reader ;-).
External Links
- Fire Bet math is discussed at my companion site Wizard of Vegas
- See my own spreadsheet, which I posted at GoogleDocs for anyone to download.
- The Doctrine of Chances: Probabilistic Aspects of Gambling by Stwart N. Ethier has a discussion of Fire Bet math.
Acknowledgements
I would like to thank Wizard of Vegas forum member Ace2 for his tireless advice on solving for the probability of the Fire Bet using integration.



