Texas Hold ’em - Probability - General
What are the odds of having two four of a kinds and a straight flush dealt to the same player in a Texas hold 'em game with ten players in 50 hands?
The probability of a four of a kind in seven cards is 0.00168067, the probability of a straight flush is 0.00027851. If x is the probability of a four of a kind and y is the probability of a straight flush then the probability you ask for is combin(50,2)*48*x2*y*(1-x-y)47. The answer comes out to .0000421845, or 1 in 23,705.
What are the statistical odds of getting a flush in Texas hold ’em. Is it easier to get a flush in 7-card stud or in holdem as a player.
You can refer to my section on probabilities in poker to see the probability is 3.03%. The odds are the same in both Texas hold ’em and 7-card stud.
What are the odds of making a royal flush in Texas hold-em on the river?
For those readers who don’t know, the river is the fifth and last community card in Texas hold-em. The player must make the best poker hand between his own two cards and the five community cards. So you’re asking what is the probability that a player will form a royal flush in seven cards, and that the seventh card dealt will be part of the royal. The probability of forming a 5-card royal flush out of 7 cards, before considering card, is 4*combin(47,2)/combin(52,7) = 4324/133784560, or 1 in 30940. The probability that the seventh card will be part of the royal flush is 5/7. So the final probability is 21620/936491920, or 1 in 43316.
In Texas Hold em, what are the odds of making a one gap or two gap inside straight by fifth street starting from the flop?
For the benefit of my readers, this question asks what is the probability of filling in a one or two gap inside straight with two more cards, with 47 left in the deck. With one gap the probability is 1-combin(43,2)/combin(47,2) = 0.164662. With two gaps the probability is 42/combin(47,2)=0.0148.
In Texas Hold ’em if the flop cards are all the same suit what is the probability any given player will hold two more cards of the same suit?
There are 10 cards left of the same suit, and 49 left in the deck. So the probability is combin(9,2)/combin(49,2) = 36/1176 = 0.0306.
Are the probabilities for the various hands the same in Texas Hold ’em as in Seven-card stud or are they different somehow due to the community cards? Could you please explain why or why not?
Yes, the probabilities are the same. Seven random cards out of 52 have the same odds regardless of how they are taken out of the deck or whom you share them with.
In the initial two cards can you tell me what the odds are of receiving 7 hands of Ace King or better at hold’em in 35 hands?
The probability of receiving ace/king is (8/52)*(4/51) = 0.012066. The probability of receiving any pair is (3/51) = 0.058824. So the probability of a pair or better is 0.07089. The probability of receiving exactly seven hands of ace/king or better is combin(35,7)*(.07089)^7*(1-.07089)^28 = 0.00772. To work out the probability of 7 or more we would have to go through a total of 7 to 35 one at a time. This adds up to 0.010366551.
How would you figure the probability of getting a 4 card flush or better on the flop in holdem, if your hole cards are suited.
The probability of getting 2 more of the same suit is 39*combin(11,2)/combin(50,3) = 0.109439. The probability of getting 3 more of the same suit is combin(11,3)/combin(50,3) = 0.008418. So the probability of getting at least 2 more of the same suit is 0.117857.
Mr. Wizard, First, let me say you have a terrific site! I’ve been reading it for a while now. I checked the poker questions, and didn’t see this one. Another site claims this, "In Texas Hold’em, the probability of AK dealt pre-flop and hitting an A or K by the river is 1 in 2 (even)." This seems intuitively way too high. What are your thoughts? Thanks again!
Thanks to you too for the kind words. For those not familiar with hold’em this question is akin to asking if a player were dealt an ace and a king plus five random cards from the remaining 50 cards, what is the probability the player would pair up the king and/or ace. Of the other 50 cards 44 of them are not kings or aces. The number of ways to draw any five cards out of 44 is combin(44,5) = 1,086,088. The number of ways to draw any five cards out of all 50 is combin(50,5) = 2,118,760. So the probability of not pairing up the ace and/or king is 1086088/2118760 = 51.26%. Thus the probability you will pair up is 1-51.26% = 48.74%. This is pretty close to 1 in 2.
What is the probability that two players will have different four-of-a-kinds in Texas Hold’em?
Between two players there are 9 total cards. These must consist of two four of a kinds and one singleton. The number of combinations for this is combin(13,2)*44 = 3432. The total number of ways to pick 9 cards out of 52 is combin(52,9) = 3,679,075,400. So the probability you have the right cards, but not necessarily in the right order, is 3432/3,679,075,400 = 1 in 1,071,992.
However just because the cards are AAAABBBBC doesn’t mean both players will have different four of a kinds. The number of ways to arrange them into a 5-card hand and two 2-card hands is 9!/(5!*2!*2!) = 756. Following are the ways those 9 cards can fall.
Four of a Kind Bad Beat Combinations
Player 1 |
Player 2 |
Flop |
Mirror Patterns |
Combinations per Pattern |
Total Combinations |
AA |
BB |
AABBC |
2 |
72 |
|
AA |
AB |
ABBBC |
4 |
48 |
192 |
AA |
AA |
BBBBC |
2 |
6 |
12 |
AA |
AC |
ABBBB |
4 |
12 |
48 |
AA |
BC |
AABBB |
4 |
24 |
96 |
AB |
AB |
AABBC |
1 |
144 |
144 |
AB |
AC |
AABBB |
4 |
48 |
192 |
Of these only the first and the fifth group result in both players having a different four of a kind. So the probability that an AAAABBBBC set of cards results in two different four of a kinds is 168/756 = 22.22%.
So the answer to your question is (3432/3,679,075,400)*(168/756) = 1 in 4,823,963. On a more practical note Party Poker has a bad beat jackpot for a losing hand of four eights. Given that there are two four of a kinds the probability that both are eights or greater is combin(7,2)/combin(13,2) = 21/78 = 26.92%. So the probability that any one hand of two players will result in this bad beat jackpot is 1 in 17,917,577.
Last night a player offered me a side wager in Texas Hold ’em. He said that at least one face card (or any three ranks) would appear on the flop and offered even money? Should I have accepted the bet?
The number of ways you can choose 3 cards out of the 40 non-face cards is (40*39*38)/(1*2*3) = 9880. The number of ways you can choose 3 cards out of 52 is (52*51*50)/(1*2*3) = 22100. So the probability of not getting a face card is 9880/22100 = 44.71%. Thus the probability of getting a face is 55.29%. His side of the bet had a 10.58% advantage.
Playing Texas Hold’em with 10 players using a standard 52-card deck, after the first two cards are dealt to each player, what are the odds that the "flop" (the next three cards) will all be the same suit? Does it make a difference if my hand has both cards of the same suit and/or each one a different suit?
Before considering your own cards the probability is 4×combin(13,3)/combin(52,3) = 5.1764706%.
Another way to look at it is the probability second card in the flop will match the first in suit is (12/51). The probability third card in the flop will match it is (11/50). (12/51)×(11/50)=5.1764706%.
The odds change a little if you consider your own cards. If you have two cards of the same suit, then the probability of a suited flop is pr(flush in same suit) + pr(flush in a different suit) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5.2193878%.
If you have two cards of a different suit, then the probability of a suited flop is pr(flush in suit in common) + pr(flush in a different suit) = 2×combin(12,3)/combin(50,3) + 2×combin(13,3)/combin(50,3) = 5.1632653%.
Dear wiz, I wish I had your brain. In any event, my struggle with stats continues. I am trying to figure out a formula to figure out the probability of getting a flush on the flop, by the turn and by the river (texas holdem) crossed by whether my hole cards are suited or not. I tried C(50,2) / C(47,5) but that didn’t work out for a suited pair by the river...I should have paid more attention in school ! Thanks ! Your biggest fan
Thanks for the kind words but I'm not that smart. A couple years ago I took the Mensa entrance exam, and didn't make the requisite top 2%. I'm still upset that they refused to tell me how well I did do. On January 13 Jeopardy tryouts are coming to Vegas, for which I have an appointment, and am sure I'll blow that too. Anyway, to answer your question here you go:
With suited hole cards:
Flush after flop: combin(11,3)/combin(50,3) = 165/19600 = 0.842%.
Flush after turn: (combin(11,2)*39/combin(50,3))*(9/47) = 2.096%.
Flush after river: (combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3.462%.
With unsuited hole cards:
Flush after flop: 0%
Flush after turn: 2*combin(12,4)/combin(50,4) = 0.430%.
Flush after river: (2*combin(12,3)*39/combin(50,4))*(9/46) = 1.458%.
Here are the commulative probabilities.
With suited hole cards:
Flush by flop: 0.842%.
Flush by turn: 2.937%.
Flush by river: 6.400%.
With unsuited hole cards:
Flush by flop: 0.000%
Flush by turn: 0.430%.
Flush by river: 1.888%.
Hi Wizard, First off I’d like to say I love the precise, fluff-free answers you give. Anyway if the pocket cards in Holdem are AA and the flop cards are KQ9, what is the probability of completing to a full house? I’ve worked on this for ages :( and still dont have an answer I trust.
You could complete the full house with an ace and a K, Q, or 9. There are 2 aces left and 3 each of K,Q, an 9. So there are 2*3*3=18 such combinations. The only other way would be a K, Q, or 9 pair. There are 3*combin(3,2)=9 such combination. The number of all combinations is 47*46/2 = 1081. So the probability is (18+9)/1081 = 2.50%.
I’ve been a huge fan for many years (even before you got interested in poker and sports betting) and looked forward to every Ask The Wizard column. It’s great to see you’re doing them again! My question is this: at my local card room, they offer Aces Cracked, Win A Rack during certain hours. That is, if you have pocket Aces in one of their 3-6 or 4-8 Texas Hold ’Em games and you lose the pot, the casino will give you a rack of chips ($100). I’m trying to figure out how often a)I get pocket Aces b)how often they would lose if I played them aggressively as I’m supposed to and c)whether it’s not better to just check all the way down and hope to lose, as $100 is usually better than what the pot would have been anyway. Any stats you may have at the ready would be wonderful and forever appreciated! Thanks again and keep up enlightening the masses!
Thanks for the kind words. The probability you will get pocket aces in any one hand is 6/1326, or once every 221 hands. According to my 10-player Texas Hold ’em section (/games/texas-hold-em/10players.html) the probability of winning with pocket aces is 31.36%, assuming all players stay in until the end. However that is a big if. If forced to make a guess I’d estimate the probability of winning with aces in a real 10-player game is about 70%. So the probability of getting pocket aces and then losing is 0.3*(1/221) = 0.1357%. So, at $100 per incident that is worth 13.57 cents per hand. Over ten people that costs the poker room $1.36 per hand on average, which cuts into the rake quite a bit. I tend to agree with your strategy of calling, which will keep more players in the hand, and increase your chance of losing.
First of all I’d like to thank you for an awsome site. Now here’s my question: We’re playing Texas hold’em and flop a flushdraw with two small cards. We all know the % of hitting the flush. but what we really want is the % of winning the hand. And let’s say that we are sure that somebody has a higher card of that suit than us. So my question is what are the % of only one card of that suit shows and not two? Regards
You’re welcome. So you have four to a flush with two on the board after the flop. The probability of getting exactly one of the needed suit is 9*38/combin(47,2) = 342/1081 = 31.64%.
In Texas Hold ’em, I’d like to know the probability that another player may have been dealt two suited cards to make a higher flush than my own when there are exactly 3 suited community cards at the river. So, for example, if I’ve got 89 of spades and the community cards include the 3 7 and K of spades, there are 4 spades larger than my 9 in the deck (TJQA). What’s the chance that someone was dealt a hand with two spades including at least one of the higher spades (assuming a 9 handed game)? What if there are only 2 (or 3 or x) spades larger than my largest hole card? Thanks for your help and the great site.
The following table shows the probability for 1 to 8 higher ranks and 2 to 10 players, including yourself. In the case of your example of 4 higher ranks and 9 total players, the probability is 16.45%. The way I calculated these probabilities assumed independence between hands, which is not a correct assumption, but the results should be a close estimate.
Probability of Higher FlushHigher Ranks (down) by Total Players (across)Wizard Estimate
| Higher Ranks | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.71% | 1.41% | 2.11% | 2.80% | 3.49% | 4.17% | 4.85% | 5.52% | 6.19% |
| 2 | 1.31% | 2.61% | 3.89% | 5.15% | 6.40% | 7.62% | 8.84% | 10.03% | 11.22% |
| 3 | 1.82% | 3.60% | 5.36% | 7.08% | 8.77% | 10.43% | 12.05% | 13.65% | 15.22% |
| 4 | 2.22% | 4.40% | 6.52% | 8.60% | 10.63% | 12.61% | 14.56% | 16.45% | 18.31% |
| 5 | 2.53% | 4.99% | 7.39% | 9.72% | 12.00% | 14.23% | 16.39% | 18.50% | 20.56% |
| 6 | 2.73% | 5.38% | 7.96% | 10.47% | 12.91% | 15.29% | 17.60% | 19.85% | 22.03% |
| 7 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
| 8 | 2.83% | 5.58% | 8.25% | 10.84% | 13.36% | 15.81% | 18.20% | 20.51% | 22.76% |
Probability of Higher FlushHigher Ranks (down) by Total Players (across)Miplet Simulation
| Higher Ranks | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.69% | 1.41% | 2.12% | 2.83% | 3.54% | 4.25% | 4.96% | 5.66% | 6.36% |
| 2 | 1.28% | 2.60% | 3.91% | 5.21% | 6.48% | 7.77% | 9.05% | 10.31% | 11.56% |
| 3 | 1.79% | 3.61% | 5.41% | 7.19% | 8.92% | 10.68% | 12.41% | 14.11% | 15.79% |
| 4 | 2.19% | 4.40% | 6.58% | 8.75% | 10.85% | 12.94% | 15.01% | 17.04% | 19.04% |
| 5 | 2.50% | 5.00% | 7.47% | 9.92% | 12.28% | 14.63% | 16.94% | 19.21% | 21.43% |
| 6 | 2.71% | 5.40% | 8.06% | 10.69% | 13.23% | 15.74% | 18.23% | 20.65% | 23.03% |
| 7 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
| 8 | 2.81% | 5.61% | 8.36% | 11.08% | 13.70% | 16.30% | 18.86% | 21.37% | 23.82% |
Great site. Asking this for my own personal knowledge. I was playing a 4 person game of texas hold’em. I was dealt pocket aces. I got the royal flush on the river. I was wondering what the odds are of making the royal flush on the river with aces to start?
Thanks. Assuming the royal consists of one of your two aces, the number of ways to make a royal by the river is 2*46=92. This would be the two suits in your pocket aces and the 46 possibilities for the extra card. There are combin(50,5) = 2,118,760 ways to deal 5 cards out of 50. So the probability is 92/2,118,760 = 1 in 23,030.
If the flop comes up three of the same suit and I do not have a suit that matches the flop, and there are ten players left at the table, what is the probability of someone having a flush?
The probability of any one player having a flush is combin(11,2)/combin(49,2) = 55/1176 = 4.68%. Assuming independence between hands, which is not the case, the probability of 9 players not having a flush is (1 − 0.0468%)9 = 64.98%. So the probability of at least one player having a flush is 1-0.6498 = 35.02%. This is just a quick estimate. If I did a random simulation I think the probability would be just a little bit higher, because of the dependence between hands.
Dear Mr. Wizard, I have been recently trying to calculate the probability of getting a flush in Texas Hold 'Em if dealt two suited hole cards? My answer keeps on coming out to be 5.8% but this seems ulimately incorrect, your help would be much appreciated thanks
The probability of making a flush, with exactly three cards to the same suit as your hole cards, is combin(11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0.057706. The probability of making a flush, with four more cards to the same suit as your hole cards, is combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0.001012. The probability of making a flush, with five more cards to the same suit as your hole cards, is combin(11,5)/combin(50,5) = 462/2118760 = 0.000218. The probability of making a flush on the board in another suit is 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0.001822. Add this all up and you get 0.057706 + 0.001012 + 0.000218 + 0.001822 = 0.060759.
What is the probability of seeing a "broken board" in Texas Hold’Em? That is, five cards on the board where no pair exists, no flush is possible and no straight is possible.
The number of combinations of five different ranks on the board is combin (13,5)*45 = 1287 × 1024 = 1,317,888.
The probability that these five ranks will represent three suits, two of two, and one of one, is combin(4,2)*2*combin(5,2)*combin(3,2)=360. Combin(4,2) is the number of ways to choose two suits out of four for the suits represented twice. 2 for the two ways to choose the suit represented once. Combin(5,2) for the number of ways to choose two ranks out of five for the first suit of two cards. 45 for the number of ways to choose two ranks out of the three left for the other suit of two.
The probability these five ranks will represent four suits, one of two, and three of one, is 4*combin(5,2)*3*2=240. 4 is the number of ways to choose one suit out of four for the suits represented twice. Combin(5,2) is the number of ways to choose two ranks out of five for that suit of two cards. 3 is the number of ways to choose one rank out of the three left for the first suit of one. 2 is the number of ways to choose one rank out of two for the second suit of one.
There are 45=1024 ways to arrange four suits on five different ranks.
So the probability that no more than two of one suit will be present is (360+240)/1024 = 600/1024 = 58.59%.
There are combin(13,5)=1287 ways to arrange 5 ranks out of 13. The number of these combinations in which no three ranks are within a span of 5 is 79. There is no easy formula for this one. I had to cycle through every combination. So the probability the ranks will be sufficiently spaced apart is 79/1287 = 6.14%.
So, the probability of a broken board is (1317888/2596960)*(600/1024)*(79/1287) = 1.825211%.
I have been challenged on my number of broken straights. Here is a list of all 79 possible.
| 2378Q 2378K 2379Q 2379K 237TQ 237TK 237JQ 237JK 237QK 2389K 238TK 238JK 238QK 2479Q 2479K 247TQ 247TK 247JQ 247JK 247QK | 2489K 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489K 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
I play Texas Hold ’Em at Caesars Indiana. They have a Bad Beat Jackpot, which is now quads or better being beat. Both players have to play both hole cards, and there must be four players dealt cards. My question is, what is the probability of any hand being a bad beat hand, assuming all players stay until the end?
My new Bad Beat Jackpot section shows the probability of this kind of bad beat in a 10-player game to be 0.0000108, or about 1 in 93,000.
In your Ultimate Texas Hold ’Em return table why is a large raise recommended for two-card hands listed in the table that have a negative expected return? For example, suited K/2.
According to my two-player Texas Hold ’Em probabilities, the following are the possible outcomes with suited K/2:
Win 51.24%
Lose 44.82%
Draw 3.94%
My table on Ultimate Texas Hold ’Em shows that the player has the advantage on the Play bet, but a disadvantage on the Ante and Blind bets. In this case, the player is stuck with bad odds on the Ante and Blind. However, his odds are favorable on the Play. So, by making the maximum raise he is getting the most value out of his better than 50% chance of winning. The bad odds on the other two bets bring the overall value under 50%. That value would be even less with a smaller raise.
In the 2008 World Series of Poker Motoyuki Mabuchi's quad aces were beaten by Justin Phillip's Royal flush. I have a simple question about the odds of this occurring. ESPN and others quoted it as 1 in approximately 2.7 billion. It appears to me that they simply took the published odds of quads occurring, and multiplied them by the odds of a royal flush occurring. Is this the correct method of calculation?
I disagree with the 1 in 2.7 billion figure too. As you said, they seemed to calculate the probabilities independently for each player, for just the case where both players use both hole cards, and multiplied. Using this method I get a probability of 0.000000000341101, or about in 1 in 2.9 billion. Maybe the one in 2.7 billion also involves compounding a rounding error on both player probabilities. They also evidently forgot to multiply the probability by 2, for reasons I explain later.
There are three ways four aces could lose to a royal flush, as follows.
Case 1: One player has two to a royal flush, the other has two aces, and the board contains the other two aces, the other two cards to the royal, and any other card.
Example:
Player 1:


Player 2:


Board:





In most poker rooms, to qualify for a bad-beat jackpot, both winning and losing player must make use of both hole cards. This was also the type of bad beat in the video; in fact, these were the exact cards.
Case 2: One player has two to a royal flush (T-K), the other has one ace and a "blank" card, and the board contains the other three aces and the other two cards to the royal.
Example:
Player 1:


Player 2:


Board:





Case 3: One player has one to a royal flush (T-K) and a blank card, the other has two aces, and the board contains the other two aces and the other three cards to the royal flush.
Example:
Player 1:


Player 2:


Board:





The following table shows the number of combinations for each case for both players and the board. The lower right cell shows the total number of combinations is 16,896.
Bad Beat Combinations
| Case | Player 1 | Player 2 | Board | Product |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3,168 |
| 2 | 24 | 132 | 1 | 3,168 |
| 3 | 704 | 3 | 1 | 2,112 |
| Total | 8,448 |
However, we could reverse the cards of the two players, and still have a bad beat. So, we should multiply the number of combinations by 2. Adjusting for that, the total qualifying combinations is 2 × 8,448 = 16,896.
The total number of all combinations in two-player Texas Hold ’Em is combin(52,2) × combin(50,2) × combin(48,5) = 2,781,381,002,400. So, the probability of a four aces losing to a royal flush is 8,448/2,781,381,002,400 = 0.0000000060747, or about 1 in 165 million. The probability of just a case 1 bad beat is 1 in 439 million. The simple reason the odds are not as long as reported in that video is that the two hands overlap, with the shared ace. In other words, the two events are positively correlated.
You are absolutely right, according to the paper Telling the Truth about New York Video Poker. The player’s outcome is indeed predestined. Regardless of what cards the player keeps, he can not avoid his fate. If the player tries to deliberately avoid his fate, the game will make use of a guardian angel feature to correct the player's mistake. I completely agree with the author that such games should warn the player that they are not playing real video poker, and the pay table is a meaningless measure of the player's actual odds. It also also be noted these kinds of fake video poker machines are not confined to New York.
Hello, I am a seventh grader from Hawaii. I am doing a science fair project on poker and shuffling. I am using your charts about the win percentage of pocket Texas Hold ’Em hands, according to the number of players in the game. I was hoping you could answer a few questions that would help me with my project:
- How did you come up with the percentages found in the charts?
- If you used a computer program, how did you develop it and how long did it take?
- You stated that you started the Wizard of Odds as a hobby. Did experimenting change as your site became more well-known? Why or why not?
- The two-player table was done by a brute-force looping program, that cycled through all 1225 possible opponent cards, and 1,712,304 possible community cards. For three to eight players, looping would have taken a prohibitive amount of time, so I did a random simulation.
- I write almost all my programs in C++, including both programs I just mentioned. The rest are in Java or PERL. I mostly copied and pasted code from other poker-based programs. The new code only look about a day to write.
- Yes, I started my site as a hobby in June 1997. It wasn’t until January 2000 that I accepted advertising, and tried to make a business out of it. It has gone through three different domains over the years. Here is what it looked like in May 1999. The purpose of the site has always remained the same, a resource for mathematically-based gambling strategy. Through the years, I have just been adding more games and material. One experiment was providing my NFL picks for the 2005 season, which was an abject failure.
Hello, Wizard. I read your Texas Hold ’Em questions, and I noticed you calculated a 59.85% chance of seeing an ace or king on the board, while holding pocket Queens. How did you come up with that figure?
There are combin(50,5)=2,118,760 combinations of five cards out of the remaining 50 in the deck. 42 of those cards are 2-Q. The number of combinations of 5 cards out of 42 is combin(42,5)=850,668. So, the probability of not getting a king or ace is 850,668/2,118,760 = 40.15%. Thus, the probability of getting at least one ace or king is 1-40.15% = 59.85%.
An alternative calculation is 1 - pr(first card in flop is not ace or king) × pr(second card in flop is not ace or king) × pr(third card in flop is not ace or king) × pr(fourth card in flop is not ace or king) × pr(fifth card in flop is not ace or king) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59.85%.
Holding two suited cards in Texas Hold ’em, what are my odds of getting exactly two more cards of the same suit on the flop?
There are combin(11,2)=55 ways to get two more cards of the same suit, and 39 for the unsuited card. There are combin(50,3)=19,600 total possible combinations of cards on the flop. So, the probability of having exactly four to a flush after the flop is 55×39/19,600 = 10.94%.
I was involved in a hand of online poker and would like to know the odds of this happening, please:
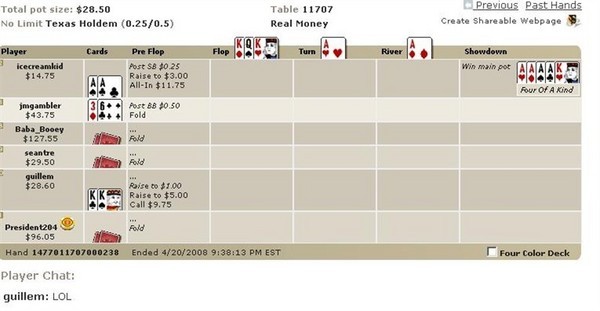
Normally I'm sick of bad beat questions, but this one was too painful to ignore. Before the first card is dealt, the probability of four kings being beaten by four aces, in a two-player game, with both players having pocket pairs, is 2*combin(4,2)*combin(4,2)*44/(combin(52,2)*combin(50,2)*combin(48,5)) = 2*6*6*44/(1326*1225*1712304) = 1 in 877,961,175. This was a six-player game, so there are combin(6,2) = 15 different player pairs. In a six-player game, the probability is 15 times higher, or 1 in 58,530,745. After the indicated hole cards are dealt, and before the flop, the probability is 1 in 38,916 that the hand will finish as it did.
There is a promotion being advertised by a Las Vegas card room: Make a flush in all four suits and you get $400. You have to use both of your hole cards, and there is a five-hour time limit. Assuming 35 hands per hour, and that the clock starts with the first flush, what is the probability of achieving the other three flushes within five hours? Thanks.
Let’s say your first flush is in spades. At 35 hands per hour, in five hours 175 hands could be played. You then have 175 hands to make a flush in hearts, diamonds, and clubs. I’m going to assume the player never folds a hand that has a possibility of attaining a flush in one of the suits he needs.
The probability of a flush of a specific suit, let’s say hearts, using both hole cards is combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0.003764605. In the next 175 hands the probability of missing a heart flush would be (1-0.003764605)175=0.51682599.
It would be incorrect to say the probability of failing to make the other three suits would be pr(no heart flush)+pr(no dimaond suit) + pr(no club flush), because you would double counting the probability of faling to make two of them. So you should add back in pr(no heart or diamond flush) + pr(no heart or club flush) +pr(no club or diamond flush). However, that would incorrectly over-subtract the probability of not making all three flushes. So you should add back in pr(no club, diamond, or heart flush).
The probability of going 175 hands and never get either of two specific suits is (1-2×0.003764605)175=0.266442448.
The probability of going 175 hands and never getting any of the three suits left is (1-3×0.003764605)175=0.137015266.
So the answer is 1-3×0.51682599 + 3×0.266442448 - 0.137015266 = 0.111834108.
I would like to thank dwheatley for his help with this problem. It is discussed on my bulletin board at Wizard of Vegas.
Doyle Brunson famously won the Main Event in the World Series of Poker in both 1976 and 1977. Each time he held 10-2 as hole cards, and both times he made a full house on the river. What are the odds of that?
Given two cards of different ranks, the probability of making a full house are 1 in 121.6. The odds of making it on the river are 1 in 207.
The odds of making such a hand on the river two out of two times is 1 in 43,006.
The odds of this happening with the same two starting cards, in rank only, are 1 in 3,564,161.
The odds of this happening with exactly 10-2 both times is 1 in 295,379,826.
Just got back from Poker Night at the VFW. Got 6-6 in the hole three times in a row! Never had that happen before. What are the odds of getting a pocket pair of the same rank three times in a row in an evening? You may assume that an evening consists of 120 total rounds.
The answer and solution appear in the following spoiler tag.
There are four possible states you can be in at any given time:
- State 1: The first hand or any hand where the last hand was not a pocket pair.
- State 2: Last hand was a pocket pair.
- State 3: Last two hands were the same pocket pair.
- State 4: Three of the same pocket pairs in a row has already been achieved.
If you're in state 1, you can advance to state 2 with a probability of 3/51. Otherwise, you stay in state 1.
If you're in state 2, you can advance to state 3 with a probability of (4/52)×(3/51). Otherwise, you go back to state 1.
If you're in state 3, you can advance to state 4 with a probability of (4/52)×(3/51). Otherwise, you go back to state 1.
If you're in state 4, you stay there.
That said, you can create your transition matrix, T, as follows:
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0.004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0.004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
There are 120 total hands played, so find T^120.
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
The upper right cell shows us the probability that starting at state 1 will lead us to state 4 after 120 starting hands in a three-hand sequence, which is 0.000141471.
Take the inverse of that number, the probability is 1 in 7068.605131.
This question is raised and discussed in my forum at Wizard of Vegas.
In the movie Casino Royale, in the final hand of a poker tournament, the four players have the following hands:
- Flush
- Full house
- Full house (of different value than first one)
- Straight flush
What is the probability of that?
I had to run a simulation for this one. In my simulation, I assume nobody ever folds. In running almost 2.2 billion rounds, this happened 312 times. That equates to a probability of about 1 in seven million.




