Sic Bo - Calculate the Odds and Win | Video
Hi guys, this is Mike.
You are going to learn how to calculate the odds in the game Sic Bo. Real briefly, Sic Bo is a very ancient Chinese game based on rolling three dice. There are a whole host of bets to choose from in the game.

What I'm going to do:
is divide this topic into two videos because everyone on my forum is complaining my videos run too long. In this first part, I am going to explain how to calculate the probability of rolling any given total from 3 to 18 with three dice, as well as the probability of rolling 0, 1, 2 or 3 of any given die face.
Once we're armed with the answers to those questions…
…we can go on to part two and analyze what kind of value you're getting with all the various different bets in Sic Bo.
Let's answer the question: "What is the probability of throwing any given total with three six-sided dice?" This technique that I'm going to show you will work for any number of dice.
I would like to give credit to Robert Goodhand of Somerset, UK for this tricky little technique here. It is covered in my Ask the Wizard column 264. I'm going to share it with you now.
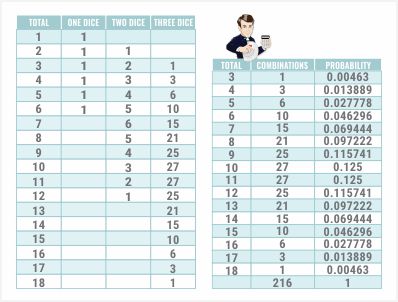
First, what we need to do is just define five dummy squares. You will see why in a minute. Now, I am going to list every total from 1 to 18. With one die, there is obviously one way to roll a 1, 2 or 6.
Each face has one side so it's pretty obvious. With two dice, what you want to do is take the sum of the column to the left, in this case, the B column, starting with one cell going to the left end up and then the five cells above that.
In the case right now…
…I'm working with cell C8. This represents the number of ways to roll a total of two with two dice. I am taking the sum of the values in cells B2 to B7. If the cell is blank, Excel correctly just assumes that it's a zero.
I just copy and paste that down through all possible totals up to 12. You will see that for a total of two, there's one way to throw it. For a total of three, there are two ways. For a total of four, there are three ways.
Well, why does this work?
Let's just consider the total of two. To get a total of two, the first die has to be a one and then the second die has to be a one. There's only one way the first die can be a one and obviously only one way the second die can be a one. For a total of three, there are two ways.
There's the one way the first die can be a one and the second die is a two, plus the one way that the first die can be a two and the second one a one. For a total of four, the first die has to be a one to a three.
For a total of five...
the first die has to be a total of one to four. As long as the first die is in that acceptable range, there is one way the next die can achieve whatever total you are talking about.
Let's go on to three dice
It is exactly the same technique. We can just copy and paste the same formula. I could take this from anywhere in the range we just did. I'll just do here, copy and paste it one cell to the right and copy and paste it down. There we have the number of combinations for any total from 3 to 18 with three dice.
For example:
There is one way to roll a total of three, three ways to roll a total of four, six ways to roll a total of five and so on. Why does this work? You may ask again. Well, let's just look at a total of seven, for example. To achieve a total of seven with three dice, that can be done if the total with two dice is two and then you add a five to it.
There's one way the first two dice can be a two. Another way can be achieved is if the first two dice total three and then the third die is a four. As we just saw, there are two ways that the first two dice can total three, there are three ways the first two dice can total four.
To get a total of seven…
…your first two dice have to be a total from two to six. We just saw that the total number of ways that can happen would be the sum here from one to five which is 15. Let's put this all in a nice handy table. Again, here is your total.
Here are the combinations:
Let's take the total of that, 216. That number looks familiar. Perhaps, it could be six to the third power.
Finally, let's find the probability of each total:
We just take the number of combinations divided by the total. There is the probability of rolling any given total from 30 to 18. Next, let's look at the probability of throwing any particular die face zero to three times. There are six different bets in Sic Bo, one for each die face.
The player wins one to one if the chosen face was rolled one time, two to one if it was rolled twice and three to one if it was rolled three times. Now, a lot of people incorrectly add probabilities when they're talking about multiple events and each die is like an independent event.
We do not add, we multiply.
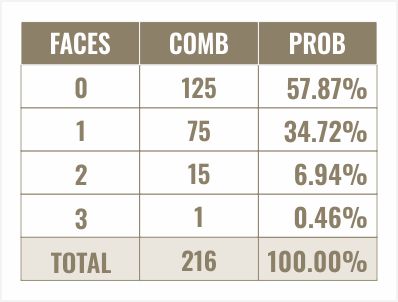
I love thinking about things in combinations first. Let's say you just pick the six, for example. What are- I should say is the number of combinations of the way that six can appear all three times on three dice? Well, it's simply one. There's only one way it can happen, 6-6-6. How about twice?
For example:
6-6-4 or 2-6-6, 6-1-6. Two of the dice are a six and one of them is something else. The something else can be any one of the five other faces and these something else can appear on any one of the three dice. The total number of ways your chosen die face can appear twice out of three dice is 15.
How about the number of ways it can appear once?
Well, the other two dice that aren't your chosen die face can be any one of five things. We multiply 5 x 5 because one of them can be anything other than a six or whatever you chose and the other one can also be any one of the other five faces.
Finally…
…we multiply by three because the one die that was your chosen face can be any one of the three dice. The number of ways you can roll your chosen face one time is 5 x 5 x 3 which is equal to 75. Examples of this would be, say you chose the face six, it could be 6-1-2, 1-4-6, 1-6-5, 2-6-2, 6-1-3, and so on.
How about the number of combinations of not rolling any of your chosen die face?
Well, each of the three dice can be one of five things. Five dice- I mean, three dice, five different combinations for each one other than your chosen face is 5 x 5 x5 combinations or 125. Let's take the total of all these combinations and we get 216 again. Again, that is six to the third power so I must have done something right.
Finally, let's look at the probability
We simply take the number of combinations divided by the total combinations. Let's put that under percent. Here we see the probability of rolling your chosen face zero times is 57.87%, once, 34.72%, twice, 6.94% and three times, 0.46%.
I hope that was clear. I hope to see you over in part two where I calculate the odds of lots of different Sic Bo bets.
Thanks for watching.
This document has been composed with the instant HTML edior tools. Click here and test it for free.




