On this page
Race the Ace
Introduction
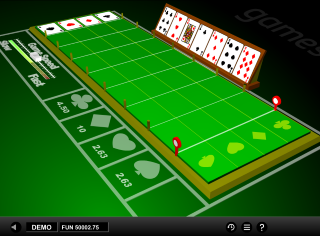
Race the Ace is a simple Derby-style racing game by 1x2 Gaming. The idea is that the player bets on a suit. Then random cards are drawn from a deck until one suit is seen eight times, at which time that suit is the winner. The player may bet before or after seven initial cards are dealt.
Returns range from 50.71% to 97.26%, depending on what bet you make, so choose your suit carefully.
Rules
- The game is played with a 48-card deck, using all cards except the aces.
- The four removed aces will be placed at the starting line of a field.
- The player may bet either "Ante Post" or "With Form."
- If the player chooses "Ante Post," then he will bet at this point on one of the four suits. Each bet shall pay 3.75 for 1 if it wins. After the player makes a bet, the first seven cards in the deck will be shown.
- If the player chooses "With Form," then the first seven cards in the deck will be revealed. The odds will then be adjusted according to how many cards are removed from each suit. The player may then bet on any suit.
- The game seems to eliminate situations where five or more of a given suit are removed, because it would then be impossible for that suit to win, for there wouldn't be enough of that suit left to reach the finish line.
- Next, the race shall begin with the remaining 41 cards, which will be revealed one at a time.
- As each card is revealed, the ace of the suit of that card shall advance one position.
- The first ace to advance eight times shall win and bets on the suit of that ace shall win.
If the player chooses to bet "With Form," then the first seven cards in the deck are revealed before the race. Of course, this changes the odds. The more cards of any given suit that are removed from the deck, the lower the chances of that suit winning, and thus the more a winning bet will pay. I've noticed that five or more cards of the same suit are never removed, for that would result in a zero chance of winning. That leaves seven other ways the suits could be distributed in the first seven cards. The following table shows those seven ways to remove seven suits and what the odds of each suit pays. All wins are on a "for one" basis, meaning the player doesn't get his original bet back on a win.
Race the Ace Pay Table
| Suit 1 Removed |
Suit 2 Removed |
Suit 3 Removed |
Suit 4 Removed |
Suit 1 Pays |
Suit 2 Pays |
Suit 3 Pays |
Suit 4 Pays |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 2.05 | 2.05 | 11 | 34 |
| 0 | 1 | 2 | 4 | 1.83 | 3 | 5.5 | 34 |
| 0 | 1 | 3 | 3 | 1.8 | 2.87 | 11 | 11 |
| 0 | 2 | 2 | 3 | 1.61 | 5.2 | 5.2 | 12 |
| 1 | 2 | 2 | 2 | 2.5 | 4.33 | 4.33 | 4.33 |
| 1 | 1 | 2 | 3 | 2.63 | 2.63 | 4.5 | 10 |
| 1 | 1 | 1 | 4 | 2.87 | 2.87 | 2.87 | 26 |
Let's look at this example. In the first seven cards on the board along the track there is one spade, one heart, three diamonds, and two clubs. That follows the "1-1-2-3" pattern of suit distribution in the table above. So, both suits with one card removed (spades and hearts) pays 2.63, the one with two removed (clubs) pays 4.5, and the one with three removed (diamonds) pays 10.
Analysis
When the player plays Ante Post, or before seeing the first seven cards, his probability of winning is obviously 25%. At 3.75 for 1 odds, the expected return is 93.75%.
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 0-0-3-4. Note the best odds are when a suit has zero missing at a pay of 2.05 and return of 94.17%.
0-0-3-4 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 0 | 2.05 | 0.459382 | 0.941733 |
| 0 | 2.05 | 0.459382 | 0.941733 |
| 3 | 11.00 | 0.064797 | 0.712767 |
| 4 | 34.00 | 0.016440 | 0.558960 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 0-1-2-4. Note the best odds are when a suit has one card missing at a pay of 3 and return of 93.68%.
0-1-2-4 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 0 | 1.83 | 0.500181 | 0.915331 |
| 1 | 3.00 | 0.312262 | 0.936786 |
| 2 | 5.50 | 0.169121 | 0.930166 |
| 4 | 34.00 | 0.018435 | 0.626790 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 0-1-3-3. Note the best odds are when a suit has zero missing at a pay of 1.8 and return of 93.86%.
0-1-3-3 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 0 | 1.80 | 0.521466 | 0.938639 |
| 1 | 2.87 | 0.326610 | 0.937371 |
| 3 | 11.00 | 0.075962 | 0.835582 |
| 3 | 11.00 | 0.075962 | 0.835582 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 0-2-2-3. Note the best odds are when a suit has two cards missing at a pay of 5.2 and return of 97.26%.
0-2-2-3 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 0 | 1.61 | 0.545564 | 0.878358 |
| 2 | 5.20 | 0.187042 | 0.972618 |
| 2 | 5.20 | 0.187042 | 0.972618 |
| 3 | 12.00 | 0.080351 | 0.964212 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 1-2-2-2. Note the best odds are when a suit has one card missing at a pay of 2.5 and return of 94.41%.
1-2-2-2 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 1 | 2.50 | 0.377634 | 0.944085 |
| 2 | 4.33 | 0.207455 | 0.898280 |
| 2 | 4.33 | 0.207455 | 0.898280 |
| 2 | 4.33 | 0.207455 | 0.898280 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 1-1-2-3. Note the best odds are when a suit has one card missing at a pay of 2.63 and return of 94.49%.
1-1-2-3 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 1 | 2.63 | 0.359279 | 0.944904 |
| 1 | 2.63 | 0.359279 | 0.944904 |
| 2 | 4.50 | 0.196660 | 0.884970 |
| 3 | 10.00 | 0.084783 | 0.847830 |
The following table shows the probability of winning, winning odds, and expected return when the seven initial cards fall in a suit distribution of 1-1-1-4. Note the best odds are when a suit has one card missing at a pay of 2.87 and return of 93.80%.
1-1-1-4 Suit Distribution
| Removed from Suit |
Pays | Probability Win |
Expected Return |
|---|---|---|---|
| 1 | 2.87 | 0.326832 | 0.938008 |
| 1 | 2.87 | 0.326832 | 0.938008 |
| 1 | 2.87 | 0.326832 | 0.938008 |
| 4 | 26.00 | 0.019503 | 0.507078 |