On this page
Minesweeper (Encrypted Version)
On this page
Introduction
This page addresses a version of Minesweeper often found at Internet casinos that are entirely based on crypto-currencies. The game is played on a 5x5 grid. The goal is to pick squares in the grid without a mine. It should not be confused with this version of the game.
Provably Fair Casinos
Rules
- The game is played on a 5x5 grid.
- The player will choose a bet and a number of mines from 1 to 24.
- The game will randomly place the number of mines chosen by the player on the grid. The placement will hidden to player at this point.
- At every decision point, the game will show how much the player's stake will increase to if his next pick is successful.
- The player will pick one of the remaining squares in the grid.
- If the player chose a square that contained a mine, then the mine will expode and the game will be over. The player will lose his stake.
- Otherwise, if the player chose a square that did not contain a mine (denoted by a Bitcoin emblem), then his stake will increase .
- The player may cash out for the amount of his stake or my pick again. If he chooses to pick again, then go back to step 5.
In the version I played, the expected return of a game was 99%, defining a game as the player either collecting or losing. The first pick had a return of 99% and all others after that in the same game had a return of 100%. I imagine this return to player is configurable.
Example
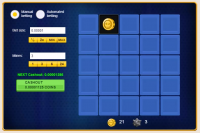
In the image above, I choose three mines and a stake of 0.00001 BTC (equivalent to about $0.10).
In the image above, I successfully chose the square in top row and second column from the left. My stake was increased to .00001076 BTC. This is based on my stake before the bet, the inverse of the probability of a successful pick of 22/25 and a 99% return: 0.00001 × (25/22) × 0.99 = 0.00001125.
In the image above, I successfully chose the square in top row and middle column. My stake was increased to .00001286 BTC. This is based on my initial stake, the inverse of the probability of a successfully making two picks, and a 99% return: 0.00001 × (25/22) × (24/21) × 0.99 = 0.00001286.
In the image above, I successfully chose the third square in top row and right column. My stake was increased to .00001479 BTC. This is based on my initial stake, the inverse of the probability of a successfully making three picks, and a 99% return: 0.00001 × (25/22) × (24/21) × (23/20) × 0.99 = 0.00001286.
In the image above, I successfully chose the fourth square in second row from the top and second column from the left. My stake was increased to .00001712 BTC. This is based on my initial stake, the inverse of the probability of a successfully making four picks, and a 99% return: 0.00001 × (25/22) × (24/21) × (23/20) × (22/19) × 0.99 = 0.00001712.
In the image above, I successfully chose the fifth square in middle row and first column from the left. My stake was increased to .00001997 BTC. This is based on my initial stake, the inverse of the probability of a successfully making five picks, and a 99% return: 0.00001 × (25/22) × (24/21) × (23/20) × (22/19) × (21/18) × 0.99 = 0.00001997.
In the image above, I successfully chose the sixth square in middle row and middle column. My stake was increased to .00002350 BTC. This is based on my initial stake, the inverse of the probability of a successfully making six picks, and a 99% return: 0.00001 × (25/22) × (24/21) × (23/20) × (22/19) × (21/18) × (20/17) × 0.99 = 0.00002350. The game shows my "next cashout," if I successfully choose another square, would be 0.00002790 BTC.
In the image above, I choose to cash out and get back 0.00002350 BTC. This consists of my original wager of 0.00001 BTC and 0.00001350 in winnings. The game shows me where the mines were placed.
In the image above, I successfully chose the fourth square in second row from the top and second column from the left. My stake was increased to .00001712 BTC. This is based on my initial stake, the inverse of the probability of a successfully making four picks, and a 99% return: 0.00001 × (25/22) × (24/21) × (23/20) × (22/19) × 0.99 = 0.00001712.
Analysis
In the version I played at CryptoGames, the return to player for the first pick was 99%. For every subsequent pick the return was 100%. The players stake is always rounded down to the 0.00000001 BTC (Bitcoin) based on the initial bet and the probability of making it to that point in the game. In other words, the rounding error is not compounded but is applied once only.
If forced to say the overall return of the game, I would say 99%, at least for the version at CryptoGames, based per bet resolved, where a bet is not resolved until lost or cashed out.
The way the Fair Gaming process works, there is a slightly higher chance a mine will be in squares 0 to 20 than 21 to 24. To be specific, the probability 1/4096 less for cells 21 to 24. This makes the return, in a one-mine one-pick game, 98.97% for picking squares 0 to 20 and 99.00% for squares 21 to 24.
Fair Gaming
This section is only for those who actually verify that the outcomes of the game was predestined. It assumes the reader is familiar with the way the "fair gaming" process works via cryptography. If you need to know the basics, I go over them in my page on Dice (Encrypted Version).
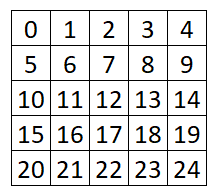
In the case of Minesweeper, the game must predestine up to 24 locations of mines on the grid. These locations are numbered as follows:
In the case of CryptoGames, the player will find the SHA512 hash of the casino's seed, followed by the number zero, followed by the player's seed. Then, to find the location of the first mine, the player will convert the first two characters in the has to decimal and take that number to the mod 25. To find the location of the next mine, the player will repeat the same process, but with the second two positions of the hash. The player will keep repeating this process, going up the hash, two positions at a time, until the location of all mines is found.
In the very unlikely event the hash runs out of positions, then the player will repeat the same process, except putting the number 1 instead of 0, between the casino's seed and player's seed, to find the additional mines.
To save you time, I wrote a Minesweeper program to easily find the location of the mines. Just enter Client Seed on line 4, the Server Seed on line 5, and click "execute code." The program will tell you were the mines are in the "Results" box below the code. I also saved a copy of the code, which you may see by clicking the button below.
$client_seed = "lKB0F28tMdLhrEn6nZ6aJGm9FSZB3bwehn47NhUk";
$server_seed = "nG1QqpFtZFoqJLMl0fE55olfP6KbptpKOInScVh9";
$mines=3;
$step=0;
$mines_found=0;
$position=0;
$combined_seed = $server_seed.$step.$client_seed;
echo "Combined seed = $combined_seed\n";
$combined_hash = hash('sha512', $combined_seed);
echo "Hash of combined seed = $combined_hash\n";
do
{
$first_two=substr($combined_hash,$position,2);
$hex_to_dec=hexdec($first_two);
$mine_location=$hex_to_dec%25;
$repeat=0;
if ($mines_found>0)
{
for ($i=0; $i<$mines_found; $i++)
{
if ( $mine_location == $mine_array[$i])
{ $repeat=1; }
}
}
if ($repeat==0)
{
$mine_array[$mines_found] = $mine_location;
$mines_found++;
echo "Mine at $mine_location\n";
}
$position+=2;
if ($position==128)
{
$position=0;
$step++;
}
}
while ($mines_found<$mines);
// Procedure
// 1. Step the "step" equal to 0 and the "position" to 0.
// 2. Join server and client seeds,step, and server seed, in that order.
// 3. Generate a SHA-512 hash of the string from step 2.
// 4. Convert first two characters, starting at the "position" of the hash from step 3 from
hexidecimal to decimal.
// 5. Divide step 4 by 25 and take the remainder.
// 6. If the result from step 5 is unique, for the game, then a mine will be located there.
// 7. Mines locations will be numbered as follows:
// 0 1 2 3 4
// 5 6 7 8 9
// 10 11 12 13 14
// 15 16 17 18 19
// 20 21 22 23 24
// 8. If all mine location have been identified then stop, otherwise, advance the "position" by 2 and go back to 4.
// 9. In the very unlikely event that the "position" reaches 128 (the end of the hash), go increment the "step" by 1, reset the "position" to 0, and go back to step 2.
?>
External Links
Discussion about Minesweeper in my forum at Wizard of Vegas.