On this page
Different Doubles
Introduction
The Different Doubles is craps side bet that has been seen at the Beau Rivage casino in Biloxi. It pays pays on the number of unique doubles the shooter rolls before rolling a total of seven. The pay table is as follow:
- 6 doubles pays 100 to 1
- 5 doubles pays 15 to 1
- 4 doubles pays 8 to 1
- 3 doubles pays 4 to 1
Analysis
The table below shows the probability and contribution to the return of all possible outcomes. The lower right cell shows a house edge of 27.92% (ouch!).
Different Doubles Return Table
| Doubles Made | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| Total | 924 | 1.000000 | -0.279221 |
Algebraic Analysis
The probability of any given double is 1/36. Thus, the probability of ANY double is 6/36 = 1/6. The probability of any seven is 1/6. We can ignore all rolls besides doubles and sevens. So, assuming there was a roll pertinent to the bet, below are the probabilities for that roll:
- Any double = 1/2
- Any seven = 1/2
The probability the first significant roll is a seven is 1/2. Thus there is a probability of zero doubles.
Otherwise, the player would have rolled a double. We can now ignore rolling that double again as a significant event. The probability of both types of significant events are now:
- Any significant double = 5/11
- Any seven = 6/11
The probability the player rolls a seven at this point, for one double, is 6/11. Thus, the overall probability of one double is (1/2)*(6/11) = 3/11 = apx. 27.27%.
Otherwise, the player would have rolled a second double. We can now ignore rolling two distinct doubles as a significant event. The probability of both types of significant events are now:
- Any significant double = 4/10
- Any seven = 6/10
The probability the player rolls a seven at this point, for two double, is 6/10. Thus, the overall probability of one double is (1/2)*(5/11)*(6/10) = 3/22 = apx. 13.6363636%.
Otherwise, the player would have rolled a third double. We can now ignore rolling three distinct doubles as a significant event. The probability of both types of significant events are now:
- Any significant double = 3/9
- Any seven = 6/9
The probability the player rolls a seven at this point, for two double, is 6/9. Thus, the overall probability of one double is (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = apx. 6.060606%.
Otherwise, the player would have rolled a fourth double. We can now ignore rolling four distinct doubles as a significant event. The probability of both types of significant events are now:
- Any significant double = 2/8
- Any seven = 6/8
The probability the player rolls a seven at this point, for two double, is 6/8. Thus, the overall probability of one double is (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = apx. 2.272727%.
Otherwise, the player would have rolled a fifth double. We can now ignore rolling five distinct doubles as a significant event. The probability of both types of significant events are now:
- Any significant double = 1/7
- Any seven = 6/7
The probability the player rolls a seven at this point, for two double, is 6/7. Thus, the overall probability of one double is (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = apx. 0.649351%.
Otherwise, the player would have rolled that last remaining double. The probability of that is (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = apx. 0.108225%.
We can now put all that together in the return table above. The number of combinations are out of 924.
Integral Calculus Analysis
Imagine that instead of significant events being determined by the roll of dice, one at a time, consider them as an instant in time. Assume the time between events has a memory-less property, with an average time between events of one unit of time. In other words, the time between events follows an exponetial distribution with a mean of 1. This will not matter for purposes of adjudicating the bet, because event still happen one at a time.
The time between specific doubles will follow an exponential distribution with a mean of 12. The reason for the 12 is if there is a significant event, there is a 1/12 chance it was that specific double. So, the probability that a specific double has not happened in x units of time is exp(-x/12). The probability it has happened is thus 1-exp(-x/12).
Let x be the number of units of time since the bet started. The probability that every double has happened and a seven has not happened is (1-exp(-x/12))6 × exp(-x/2).
To close that off with a roll of a 7 at time x, multiply that by 1/2, the probability of a 7, to get a probability of a winning get at exactly time x of (1/2) ×(1-exp(-x/12))6 × exp(-x/2)
To find the probability of a winning bet over all time, integrate from 1 to infinity:
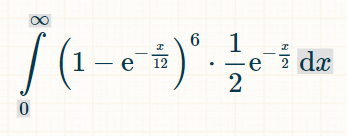
To integrate that, I recommend this integral calculator. In the integral field put, "(1-exp(-x/12))^6*(1/2)*exp(-x/2)." For the limits of integration, under options, put 0 and ∞. Then click "go." It will give you the integral below:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40*(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
However, we don't need to enter 0 into that. The calculator gives the answer as 1/924 = apx. 0.001082251082251082.
Here is the integral for five different doubles. The reason for the 6 is there are 6 possible doubles that were not made:
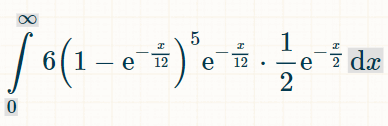
Here is the probability of winning within x units of time:
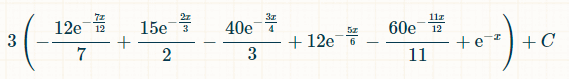
Putting in the bounds of integration from 0 to infinity, the probability of rolling exactly five distinct doubles is 1/154.
Here is the integral for four different doubles. The reason for the 15 is there are 6!/(4!*2!) = 15 possible combinations of 4 out of 6 doubles that were made:
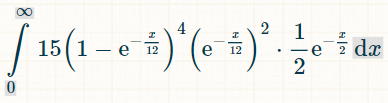
Here is the probability of winning within x units of time:
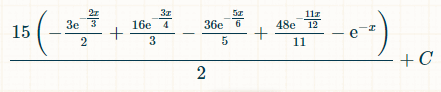
Putting in the bounds of integration from 0 to infinity, the probability of rolling exactly four distinct doubles is 1/44.
Here is the integral for three distinct doubles. The reason for the 20 is there are 6!/(3!*3!) = 20 possible combinations of 3 out of 6 doubles that were made:
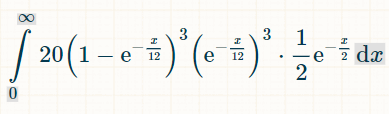
Here is the probability of winning within x units of time:
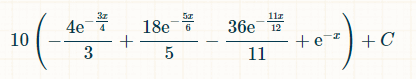
Putting in the bounds of integration from 0 to infinity, the probability of rolling exactly three distinct doubles is 2/33.





