WOO logo

Wizard Recommends

Ask The Wizard #427

A cake is split as follows:

  • The first person gets 1%
  • The second person gets 2% of what's left
  • The third person gets 3% of what's left
  • And so on.

Which person will get the most cake? No spreadsheets or brute force calculations allowed.

anonymous

The 10th person will get the most cake.

 

Here is my solution (PDF).

This question is asked and discussed in my forum at Wizard of Vegas.

I would like to give credit to the Mind Your Decisions YouTube channel for this math puzzle.

 

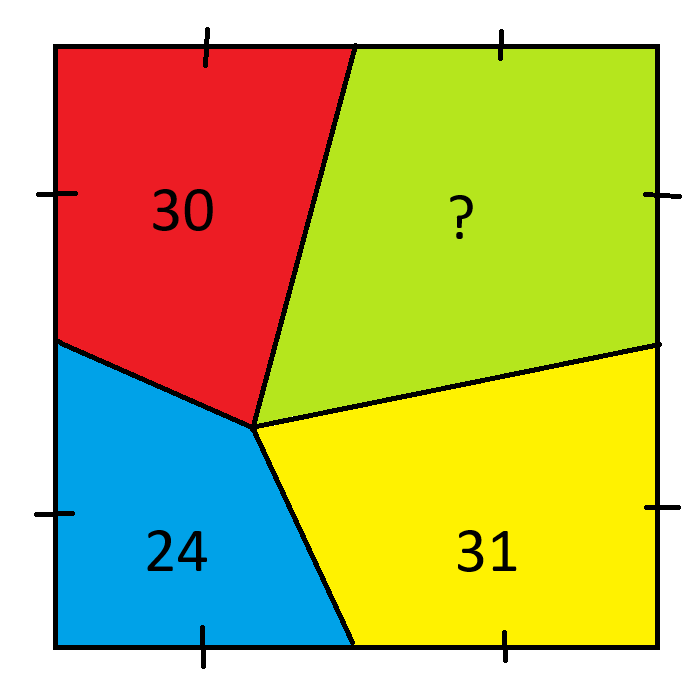
What is the area of the green region?

anonymous

38

 

First, draw four lines from the intersection of the four pieces to each corner. Then label the eight pieces as follows.

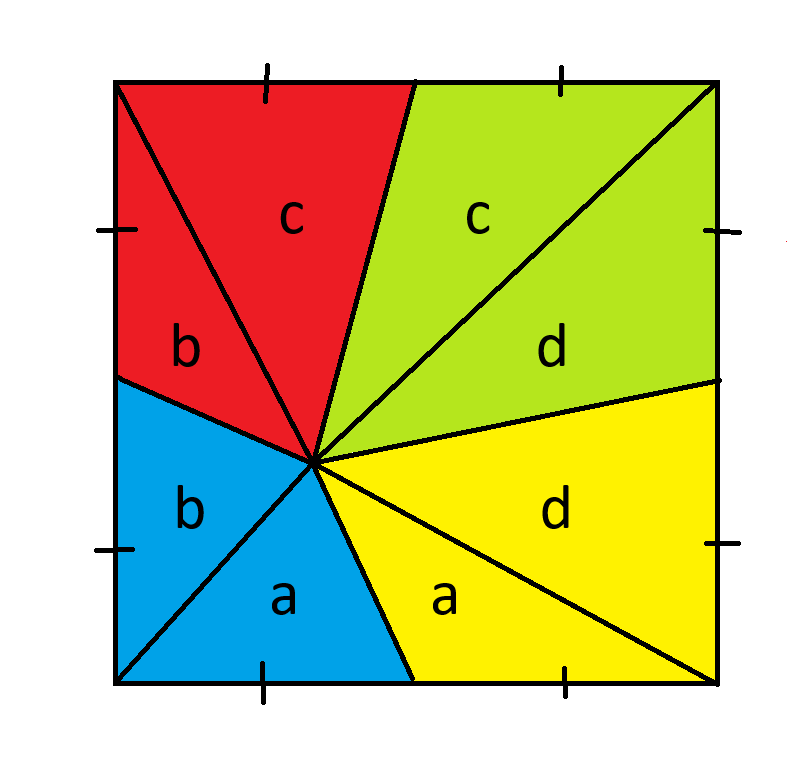
Recall the area of a triangle is base*height/2. Since all triangles have the same base we can match triangles equal in height as having the same area.

At this point we know:

  • (1) A+B = 34
  • (2) B+C = 42
  • (3) A+D = 30

Adding equations (2) and (3):

A+B+C+D = 72

Let's subtract out equation (1) from that:

C+D = 38, which is our answer.

This question was asked and discussed in my forum at Wizard of Vegas.

The source of the puzzle is the YouTube video titled "98% FAILED to Solve this Math Problem."

Let's say you want to find the mean of several values. What is your opinion of dropping the highest and lowest values, like they do for gymnastics scoring in the Olympics? Let's say the purpose is to find the mean value per square foot of a particular neighborhood.

anonymous

Good question. What you're talking about is called the trimmed mean. I'm not aware of a statistic for the variance of the trimmed mean from the true mean. Lacking any better idea, I did my own experiment.

To answer your question, I took 100,000 samples of ten sets of values. Each value was distributed according to the standard normal distribution, meaning a mean of 0 and variance of 1. I then looked at the mean of all ten values as well as the mean of the trimmed eight.

What I found was the average difference between the sample mean and true mean sampling all ten values was 0.003450. Doing the same thing, but taking the average of the trimmed mean had an average difference of 0.003445. In my opinion, this is not a significant enough difference to declare which method is better. Also, what might be right for my experiment might not be for another application.

In conclusion, it isn't often I say this, I don't have a definitive mathematical answer.

What is the more efficient (meaning least wasted space) way to stack spheres, with a square or triangular base?

 

 

anonymous

The way I answered this was which pyramid had the greatest ratio of volume of spheres to the volume of the pyramid enclosing them as the number of spheres approached infinity.

They are equally efficient, with efficiency of 74.05%.

 

Here is my solution (PDF).

I later realized this question was also asked in Ask the Wizard #350. However, I think this solution is better.