Ask The Wizard #353
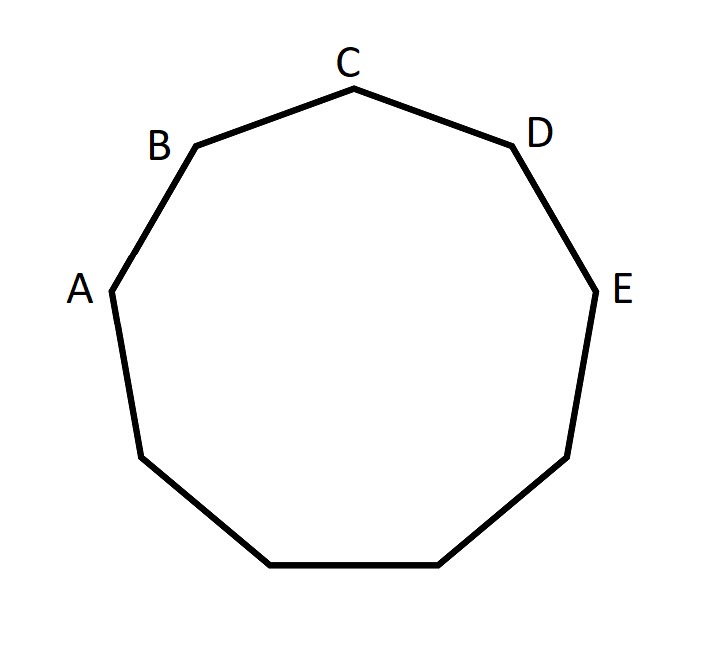
The figure above is a nonagon with side length one.
Which is more, AB+AC or AE?
This problem was taken from the March 2021 issue of the Mensa Bulletin.
Here is my solution to this problem. (PDF)
How can I easily find the square root of any three- or four-digit number, assuming the answer is an integer?
The following table shows the numbers 0 to 9, the square of each and the last digit of that square.
Last Digit of Square Numbers
| Original Number |
Square | Last digit of Square |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Note that numbers are even squares always end in 0, 1, 4, 5, 6, or 9. This is true for all squares. This is because the last digit of the original number determines the last digit of the square.
Step 1: Based on the last digit of the square, we can use the following table to narrow down the last digit of the square root. For example, if 2809 is the square, then the last digit of the square root is 3 or 7.
Last Digit of Original Number
| Last digit of Square Root |
Last digit of Square |
|---|---|
| 0 | 0 |
| 1 | 1 or 9 |
| 4 | 2 or 8 |
| 5 | 5 |
| 6 | 4 or 6 |
| 9 | 3 or 7 |
Step 2: Next, take the original number and drop the right two digits. For example, if the original number were 2809, then use 28.
Step 3: Find the smallest square number less than or equal to the result of step 2. Then, take the square root of that square number. For example, the smallest square less then 28 is 25. Take the square root of 25 and you get 5.
If you haven't memorized the squares up to 100, then you may use the following table.
First Portion of Square Root
| Step 2 | Step 3 |
|---|---|
| 1 to 3 | 1 |
| 4 to 8 | 2 |
| 9 to 15 | 3 |
| 16 to 24 | 4 |
| 25 to 35 | 5 |
| 36 to 48 | 6 |
| 49 to 63 | 7 |
| 64 to 80 | 8 |
| 81 to 99 | 9 |
Step 4: If the result from step 1 is a 0 or 5, then put that after the result from step 3 and you're done.
Otherwise, let a = result from step 3. Let b=a×(a+1). For example, if the result from step 3 where 5, then b=5×6=30.
Step 5: If b < a, then the final digit of the square root is the lesser of the possibilities from step 1. Otherwise, if b >= a, then it is the greater of the two possibilities.
Step 6: To get the square root, take the result from step 3 and then follow it with the result from step 5. In other words 10×(step 3)+step 5.
Let's look at some examples:
Find the square root of 256.
- Step 1: The last digit of the square root is 4 or 6.
- Step 2: Dropping the last two digits, we get 2.
- Step 3: The smallest square less than or equal to 2 is 1. The square root of 1 is 1.
- Step 4: 1*(1+1) = 2.
- Step 5: The result from step 4 is equal to that of step 2, so we use the larger of the options from step 1 as the last digit, which is 6.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 1 & 6 = 16.
Find the square root of 1369.
- Step 1: The last digit of the square root is 3 or 7.
- Step 2: Dropping the last two digits, we get 13.
- Step 3: The smallest square less than or equal to 13 is 9. The square root of 9 is 3.
- Step 4: 3*(1+3) = 12.
- Step 5: The result from step 2 is greater than that of step 4, so we use the larger of the options from step 1 as the last digit, which is 7.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 3 & 7 = 37.
Find the square root of 2704.
- Step 1: The last digit of the square root is 2 or 8.
- Step 2: Dropping the last two digits, we get 27.
- Step 3: The smallest square less than or equal to 27 is 25. The square root of 25 is 5.
- Step 4: 5*(1+5) = 60.
- Step 5: The result from step 2 is less than that of step 4, so we use the smaller of the options from step 1 as the last digit, which is 2.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 5 & 2 = 52.
Find the square root of 5625.
- Step 1: The last digit of the square root is 5.
- Step 2: Dropping the last two digits, we get 56.
- Step 3: The smallest square less than or equal to 56 is 49. The square root of 49 is 7.
- Step 4: The result from step 1 is a 0 or 5, so the answer is the result from step 3 appended by that of step 1: 7 & 5 = 75
Find the square root of 6561.
- Step 1: The last digit is 1 or 9.
- Step 2: Dropping the last two digits, we get 65.
- Step 3: The smallest square less than or equal to 65 is 64. The square root of 64 is 8.
- Step 4: 8*(1+8) = 72.
- Step 5: The result from step 2 is less than that of step 4, so we use the lesser of the options from step 1 as the last digit, which is 1.
- Step 6: The square root is the result from 3 appended by the result from step 5, which comes to 8 & 1 = 81.
You may see a demonstration of this method on YouTube.
In 12 hours of blackjack play, what is the probability of seeing 60 or more wins in a row?
According to my variance in blackjack page, based on liberal Strip rules, the following are the probabilities of a net win, push, or loss:
- Win — 42.43%
- Push — 8.48%
- Loss — 49.09%
Let's ignore the ties, giving us a probability of winning, given the hand resolved in a net win or loss, of 46.36%.
Let's use 100 hands per hour as a playing speed.
We can approximate the probability of seeing at least one streak of at least 60 hands in a row as:
100×12×0.463660 = 1 in 89,412,355,233,588,500.As a basis of comparison, if you purchased on Powerball and one Megamillions ticket, the probability of winning both would be 1 in 88,412,922,115,818,300.
So it would be a little more likely to win both lotteries than to see 60 wins in a row in 12 hours of play.




