Wizard Recommends Cards

Ask The Wizard #343

In your page titled My Methodology for Video Poker Analysis, you state to analyze video poker there are only 134,459 types of equivalent hands, compared to the 2,598,960 possible five-card hands on the deal.

That is for a single deck game. I have heard of a video poker game called Aces Live that uses six decks. How many classes of five-card hands are there with six decks?

robomb162

It isn't often I need help with a gambling question, but Gary Kohler kindly did the hard work to answer this one. The following table shows Gary's number of classes of hands for one to six decks.

Video Poker Classes of Hands

Decks Total
Combinations		 Total
Hand Classes
1 2,598,960 134,459
2 91,962,520 202,735
3 721,656,936 208,143
4 3,091,033,296 208,468
5 9,525,431,552 208,481
6 23,856,384,552 208,481

This question is asked and discussed in my forum at Wizard of Vegas.

What is the probability of a four-, five-, and six-of a kind in baccarat, combining all the cards that were dealt between the Player and Banker hand, for all 13 ranks?

anonymous

The following table shows the number of permutations for all four-, five-, and six-of a kinds in baccarat by rank out of a possible 4,998,398,275,503,360 permutations.

Keno 4-6 of a Kind Permutations in Baccarat

Rank 4 of a Kind 5 of a Kind 6 of a Kind
Ace 1,174,231,511,040 40,210,759,680 652,458,240
2 1,130,651,443,200 36,344,340,480 652,458,240
3 840,162,535,680 - -
4 431,482,026,240 - -
5 1,201,241,210,880 43,303,895,040 652,458,240
6 1,079,228,067,840 40,210,759,680 652,458,240
7 986,765,414,400 30,158,069,760 652,458,240
8 502,955,546,880 - -
9 230,538,696,960 - -
10 1,174,176,276,480 40,210,759,680 652,458,240
Jack 1,174,176,276,480 40,210,759,680 652,458,240
Queen 1,174,176,276,480 40,210,759,680 652,458,240
King 1,174,176,276,480 40,210,759,680 652,458,240
Total 12,273,961,559,040 351,070,863,360 5,872,124,160

The following table shows the probability for all four-, five-, and six-of a kinds in baccarat by rank.

Keno 4-6 of a Kind Probabilities in Baccarat

Rank 4 of a Kind 5 of a Kind 6 of a Kind
Ace 0.0002349216 0.0000080447 0.0000001305
2 0.0002262028 0.0000072712 0.0000001305
3 0.0001680864 0.0000000000 0.0000000000
4 0.0000863241 0.0000000000 0.0000000000
5 0.0002403252 0.0000086636 0.0000001305
6 0.0002159148 0.0000080447 0.0000001305
7 0.0001974163 0.0000060335 0.0000001305
8 0.0001006233 0.0000000000 0.0000000000
9 0.0000461225 0.0000000000 0.0000000000
10 0.0002349105 0.0000080447 0.0000001305
Jack 0.0002349105 0.0000080447 0.0000001305
Queen 0.0002349105 0.0000080447 0.0000001305
King 0.0002349105 0.0000080447 0.0000001305
Total 0.0024555789 0.0000702367 0.0000011748

A cuboid is a three-dimensional block, composed of unit-squares.

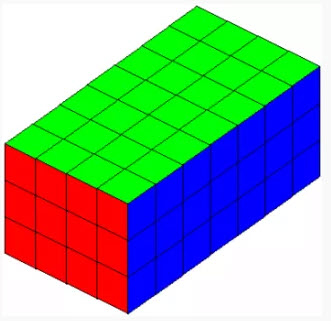
cuboid

An a × b × c cuboid is constructed out of abc identical unit cubes, like a 3x3x3 Rubik's Cube. Divide the cubes into two mutually exclusive types. External cubes are those that constitute the faces of the cuboid; internal cubes are completely enclosed. For example, the cuboid pictured has 74 external and 10 internal cubes.

Give the dimensions of all cuboids such that the number of external cubes equals the number of internal cubes.

Gialmere

There are 20 possible such cuboids.
  1. 5 X 13 X 132
  2. 5 X 14 X 72
  3. 5 X 15 X 52
  4. 5 X 16 X 42
  5. 5 X 17 X 36
  6. 5 X 18 X 32
  7. 5 X 20 X 27
  8. 5 X 22 X 24
  9. 6 X 9 X 56
  10. 6 X 10 X 32
  11. 6 X 11 X 24
  12. 6 X 12 X 20
  13. 6 X 14 X 16
  14. 7 X 7 X 100
  15. 7 X 8 X 30
  16. 7 X 9 X 20
  17. 7 X 10 X 16
  18. 8 X 8 X 18
  19. 8 X 9 X 14
  20. 8 X 10 X 12

This question is asked and discussed in my forum at Wizard of Vegas.