Ask The Wizard #322
I sat down at a game of Texas Hold 'Em and the high hand during the hand in progress was a straight flush. Two other players at the table remarked it was the third straight flush in a row. What are the odds of that?
In a 10-player game of Texas Hold 'Em, assuming nobody ever folds, the probability that the high hand will be a straight or royal flush is 1 in 350.14. The probability of this happening three hands out of three is 1 in 42,926,491.
However, that table may have been going for hours. Perhaps a more realistic question is what is the probability that would happen at least once in an entire day. Assuming a full 24 hours of play and 24 hands per hour, the answer to that question would be 1 in 59,621.
This question is asked and discussed in my forum at Wizard of Vegas.
Assuming proper strategy, what is the probability of winning given a 4x raise in Ultimate Texas Hold 'Em? I recorded 96 4x hands. Not counting pushes, I had 66 wins and 30 losses. How does that compare to expectations?
Assuming correct 4x raising strategy, there is the probability of each outcome, given a 4x raise:
- Win: 58.82%
- Loss: 38.47%
- Tie: 2.72%
If we factor out the ties, the probability of winning is 60.46%. In 96 hands resolved, the expected number of 4x wins is 58.04. So, 66 wins is ahead of expectations, but not significantly.
This question is asked and discussed in my forum at Wizard of Vegas.
Axel and Bob each have his own 52-card deck. Both shuffle them randomly. They then turn over one card at a time, simultaneously, from each deck. What is the probability that they turn over the same card at the same time at least once?
It would be easily to estimate the answer as 1-(51/52)52 = 0.63568648. However, estimates are so intellectually unsatisfying. So, let's find an exact solution!
Step 1: To start, consider the number of ways the second deck can be ordered where the first card is number 1. The answer is the number of ways to order the other 51 cards, which is 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Any card can match the first deck, so we must do this for all 52 cards. This gives us 52*51! = 52! combinations where at least one card matches.
Step 2: However, step 1 double counts every situation where two cards match. For example, if the first two cards were 1 and 2, we would have counted the 50! ways to arrange the other cards twice, once for 1 as the first card and a second time for 2 as the second card. The number of ways to choose 2 cards out of 52 is combin(52,2) = 1326. For each combination of two cards, there are 50! = 30414093201713378043612608166064768844377641568960512000000000000 ways to order the other cards. Thus, for step 2 we need to subtract out combin(52,2)*50! = (52*51/2!)*50! = 52!/2! combinations.
Step 3: Next, consider the situation where the first three cards in the random deck are 1, 2, and 3 in order. There are 49! ways to order the other 49 cards. We would have counted them three times in the initial step of counting for at least one matching card. Then we would have subtracted out all combin(3,2)=3 ways to choose 2 out of these three cards in the second step. So this situation would have been counted 3-3=0 times, so we need to add them back in. There are combin(52,3) such situations of choosing at least 3 cards that match. So we need to add back in combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! combinations back in.
Step 4: Next, consider the situation where the first four cards in the random deck are 1, 2, 3, and 4 in order. There are 48! ways to order the other 48 cards. We would have counted them four times in the initial step of counting for at least one matching card. Then we would have subtracted out all combin(4,2)=6 ways to choose two out of these four cards in step 2. Then we would have added all combin(4,3)=4 ways to choose 3 out of these four cards. So we are at 4-6+4=2 ways each such situation would have been counted. So we need to subtract one of those ways out, so that each situation will be counted once. There are combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! such situations that need to be added back in.
We will keep doing this, alternating adding and subtracting to correct for double counting.
In the end, the number of situations where at least one card in the random deck matches the ordered deck = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
There are 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 total ways to order 52 cards.
Thus, the answer is x/y = 0.6321205588285576784044762298
The probability that there are no matches is 1-(x/y) = 0.3678794411714423215955237702.
If this number looks familiar, it should. 1/e = 0.3678794411714423215955237702.
So, the answer can be VERY closely estimated as 1-(1/e).
Acknowledgements
Mathematical calculations were done in Pari/GP
This problems was asked and discussed in my forum at Wizard of Vegas.
In the document titled bingo pattern probabilities (PDF) on your site, you indicate the expected number of calls to find a winner, assuming 300 cards in play, is as follows:
- Four corners: 8.43
- Small diamond: 11.833
Both patterns require four marks only and have only one way to win. Why are the expected number of balls to find a winner different?
This is a difficult answer to explain. Let me start by saying that expected number of calls in a single-card game would be the same. However, there is a correlation effect with more than one card.
It's hard to give a quick answer to this one, but if forced, it's because the four corner pattern requires a concentration of balls in the B and O columns. The small diamond pattern is more likely to be hit with a flatter distribution of balls over the B, N, and O columns.
Let's simplify the game to one where there are an infinite number of cards in play and the balls are drawn WITH replacement. Here is the number of balls required to get a winner in both games:
- Four corners: 2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- Small diamond: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
This shows that the four corners takes 1.53 more balls.
Running this through a simultion under normal bingo rules, assuming infinite cards, here are the results:
- Four corners: 12.8289
- Diamond: 11.3645
This time a different of 1.46 balls.
What I hope to have shown is patterns are more likely to be covered quicker if the marks are distributed over more columns. For this reason, I think that in a single-bingo game you usually see the winning bingo is horizontal.
This question is asked in discussed in my forum at Wizard of Vegas.
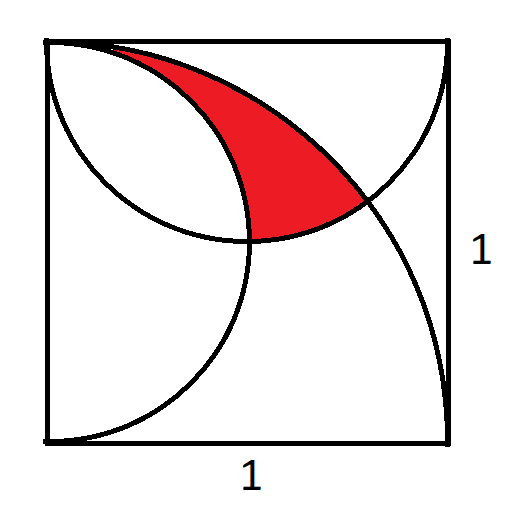
In the figure above, there is a quarter-circle and two semi-circles in a square of side length one. The question is what is the area of the red region?
Click the following button for my answer.
Click the following button for my solution.
Here is a link to my solution. (PDF)
This question is asked and discussed in my forum at Wizard of Vegas.
Acknowledgements: I would like to thank Mind Your Decisions for this math puzzle.




