Sum of First n Integers Proof

This week I do one of my easier proofs, that 1+2+3+…+n = n(n+1)/2. I show it two very intuitive ways. My easiest proof thus far. However, before we get to that, I present my usual weekly logic puzzle.

Logic Puzzle

Alice, Bob and Cole make the following statements:

1. • Alice: Bob is a liar.
2. • Bob: Cole is a liar.
3. • Cole: Alice and Bob are liars.

 

All three either always tell the truth or always lie. They all know the truthfullness of the other two. Who is telling the truth?

See the end of the newsletter for the answer and solution.

Sum of First n Integers Proof

Everybody should know that the sum of the first n integers is n(n+1)/2. In other words, 1+2+3+…+n = n(n+1)/2. I present two simple proofs why this is true.

Method 1

It’s easy to see the average number in the sequence is (n+1)/2. The number of terms in the series is n. The sum is equal to the product of the number of terms and the average term = n × (n+1)/2 = n(n+1)/2.

This same method can be used to find the sum with any starting and ending point. Let’s call the starting number a and the ending number b. The average will be (a+b)/2. The number of terms will be (a-b+1). So the sum of all numbers in the series will be (a-b+1) × (a+b)/2.

Method 2

The next method is easier explained visually. Consider the following diagram where the blue squares illustrate the integers from 1 to 5.

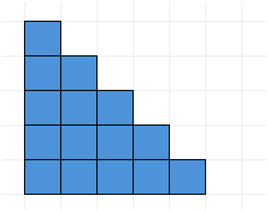
Next, duplicate it place it next to the original piece as follows, making a rectangle.

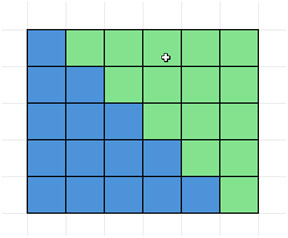
Notice how the dimensions of the above rectangle are 5 × 6. In the general case, of adding the integers from 1 to n, the dimensions are n × (n+1). Then divide that area by 2 because we seek the area of one of the two pieces only. Thus, the area of a single piece is n(n+1)/2.

Logic Puzzle Solution

All three people have two possible states, truthful or lying. That makes 2³ = 8 possibilities. I list all of them in the table below.

Scenario	1	2	3	4	5	6	7	8
Alice	T	T	T	T	F	F	F	F
Bob	T	T	F	F	T	T	F	F
Cole	T	F	T	F	T	F	T	F

 

Note that Bob and Cole call each other liars. The only way that is possible is if one of them is truthful and the other is a liar. So, we can eliminate the four situations where Bob and Cole have the same truthfulness. That leaves scenarios 2, 3, 6 and 7. Let’s examine them one at a time.

In scenario 2, it is given Alice is truthful. Her true statement makes Bob a liar. However, Bob is also truthful in this scenario, which leads to a contradiction. Thus scenario 2 is out.

In scenario 3 it is given that Alice is truthful. She says Bob is a liar, which is true under the scenario 3 assumptions. However, Cole is listed as truthful, who says Alice is lying. Alice cannot be truthful and a liar at the same time, so scenario 3 is out.

In scenario 7 it is given that Alice is lying. She says Bob is a liar, which is true. However, that would make Alice truthful. Alice can’t be truthful and a liar at the same time, so scenario 7 is out.

That leaves just scenario 6. Let’s make sure it works. If Alice were a liar, that would make Bob truthful. If Bob were truthful, then Alice or Bob or both would be truthful. Bob is truthful so that makes Cole’s statement false. So, it holds water. Bob is the only truthful person.