Sum of Angles in a Triangle Equals 180 Degrees Theorem

It should be common knowledge that the sum of the interior angles of any triangle is 180 degrees. In this newsletter, I will present a simple proof. However, before that, I present the usual weekly logic puzzle.

Logic Puzzle

A king has 49 gold coins. The coins weigh 1, 2, 3, ... 49 grams each. How can he divide them among seven sons so that each son gets seven coins such that the sum of the weights is equal?

Proof that the interior angles of any triangle sum to 180 degrees.

I’ll begin by drawing an arbitrary triangle and labeling the angles.

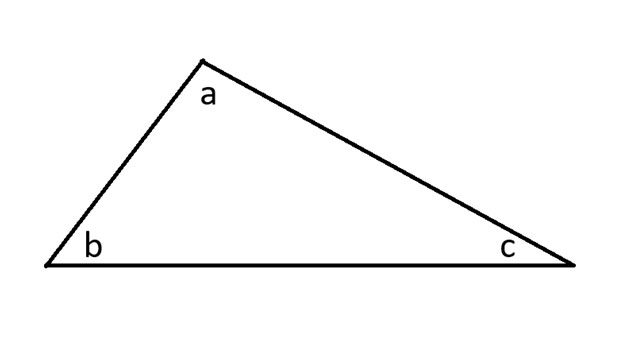
Next, I’ll extend all three sides of the triangle as well as raw a parallel line that touches angle a.

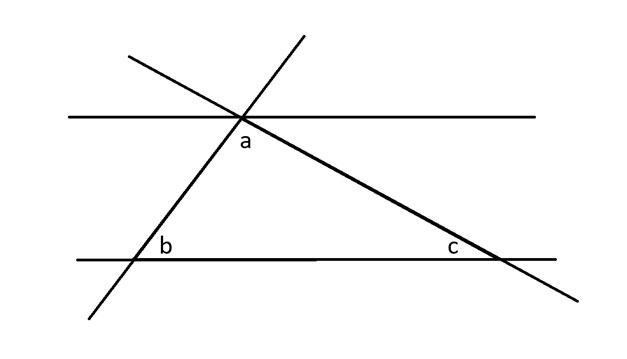
Next, I’ll apply the opposite angle theorem to angle b, which says that the angles at opposite corners of two intersecting lines are equal.

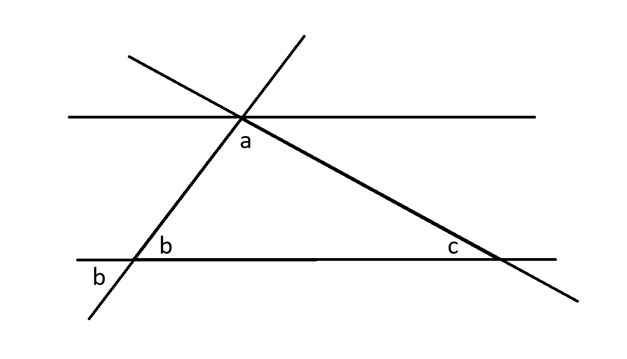
When a diagonal cuts across a set of parallel lines, it creates the same angles where it crosses each line. I apply that to show another angle of b degrees next to angle a. Then I do the same thing with angle c.

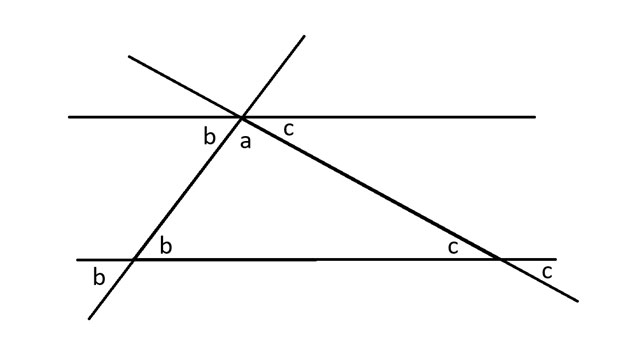
There are 360 degrees in a circle. Thus, there are 180 degrees in half circle. In other words, looking at the angles at the bottom of the top parallel line, a + b + c = 180 degrees. These are also the three angles of the original triangle. Thus, the sum of the angles in a triangle equals 180 degrees.

Logic Puzzle Solution

Make a magic square and give each son the coins in any one column. You may also divide the coins by rows. “How do you make a 7x7 magic square?”, you might ask. The following is known as the Siamese Method and was discovered in India a long time ago.

Let’s start with a grid labeled like a 7x7 Battleship board.

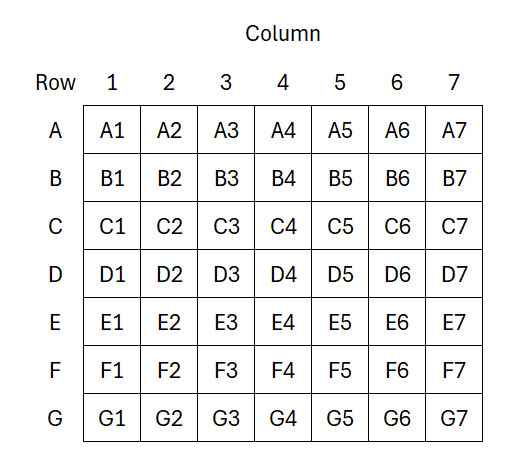
Start with a 1 in cell A4. Then follow these rules:

1. Always add 1 to the previous number for the next placement.
2. Always go in a northwest direction, unless that space is occupied or you are already on row A or column 7.
3. If you are on row A, then wrap around to column G for the next number.
4. If you are on column 7, then wrap around to column 1 for the next number.
5. Call A7 will wrap around both ways to G1.
6. If the next square you should go to is occupied, then drop down to the next square for the next number (it should be empty).

 

Here is how we start:

1. 1 in cell A4.
2. We are in row A, so wrap around to row G, putting a 2 in cell G5.
3. We then put a 3 in F6, 4 in E7.
4. We are at column 7, so we wrap around, putting a 5 in D1.
5. Put a 6 in C2, 7 in B3.
6. We next would come to A4, but it is occupied with a 1. So, we drop down and put the next number, an 8, in C3.
7. Keep repeating until the Magic Square is full.

 

Here is what it will look like when completed:

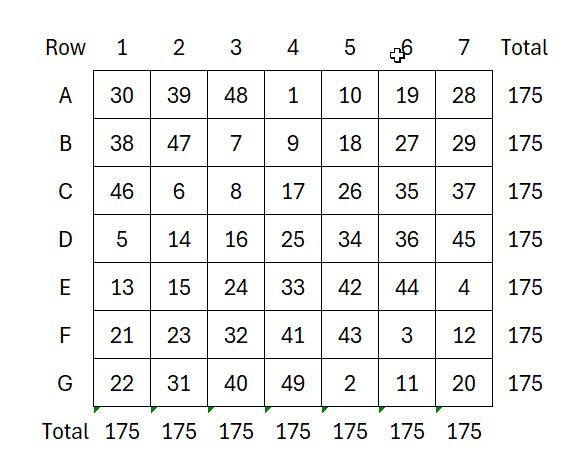
This method will work for any magic square of odd-numbered dimensions.

Then, decide whether you are going to divide by rows or columns. Each each son the coins found in one of the rows/columns. For example, if you go by columns, son 1 would get the 30, 38, 46, 5, 13, 21 and 22 coins.