Round Robin Scheduling
This week’s topic will be how to schedule a round robin tournament. Before I go further, a round robin is a tournament format in which every player plays every other player. In a tournament with n players, the number of matches will be n(n-1)/2.
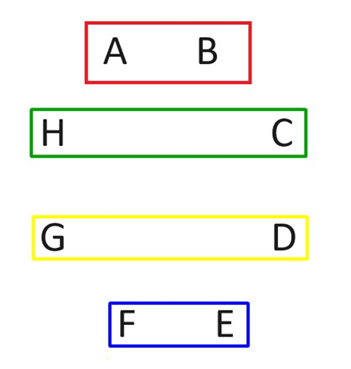
It would be easy to list out all n(n-1)/2 possible pairings among n players. However, it is ideal to do so in rounds, where every player plays once in each round. Here is how to do that with an even number of players. Let’s use the eight-player situation as an example. In the following image, we label the players A to H and show the two players in a match in the four rectangles. These four games will constitute the first round. Notice how everybody plays.
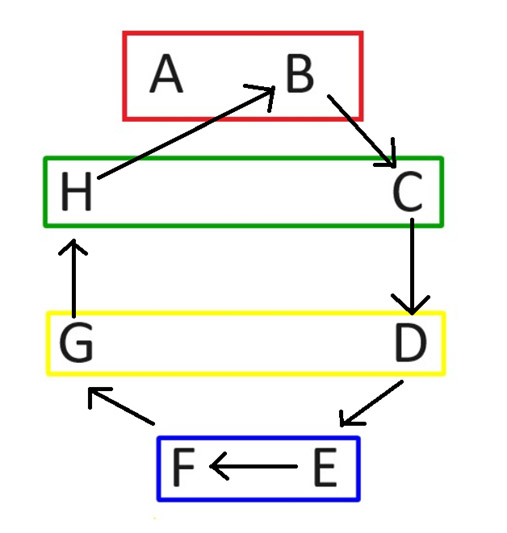
In the second round, keep player A in the same position. Then rotate everybody else clockwise, as shown in the following diagram.
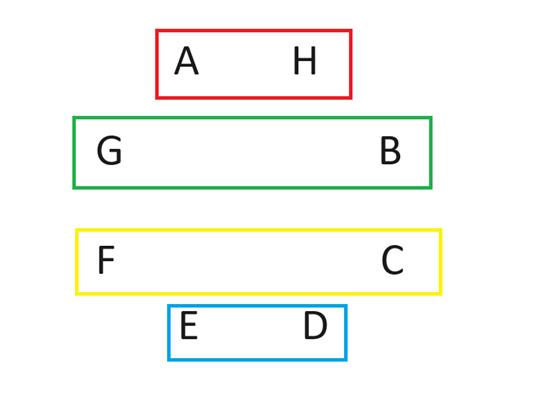
After the rotation, the second round of matches will look as follows:
Keep doing this until everybody has played against player A. I can’t explain why this works, but it just does. It works for any even number of players. For further discussion about it, search on “circle method” and “round robin.”
The following table shows all matchups in the eight-player case. Notice how everybody plays everyone else exactly once.
| Round | Player 1 | Player 2 |
|---|---|---|
| 1 | A | B |
| 1 | H | C |
| 1 | G | D |
| 1 | F | E |
| 1 | A | H |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | A | G |
| 3 | F | H |
| 3 | E | B |
| 3 | D | C |
| 4 | A | F |
| 4 | E | G |
| 4 | D | H |
| 4 | C | B |
| 5 | A | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | H |
| 6 | A | D |
| 6 | C | E |
| 6 | B | F |
| 6 | H | G |
| 7 | A | C |
| 7 | B | D |
| 7 | H | E |
| 7 | G | F |
For an odd number of players, simply add a dummy player to the tournament, to get an even number. Whoever plays against the dummy player gets a bye that round, meaning they skip playing. So, everybody will have one round where they sit out. Here is what that would look like in a seven-player tournament.
| Round | Player 1 | Player 2 |
|---|---|---|
| 1 | A | B |
| 1 | bye | C |
| 1 | G | D |
| 1 | F | E |
| 2 | A | bye |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | A | G |
| 3 | F | bye |
| 3 | E | B |
| 3 | D | C |
| 4 | A | F |
| 4 | E | G |
| 4 | D | bye |
| 4 | C | B |
| 5 | A | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | bye |
| 6 | A | D |
| 6 | C | E |
| 6 | B | F |
| 6 | bye | G |
| 7 | A | C |
| 7 | B | D |
| 7 | bye | E |
| 7 | G | F |
Finally, suppose that this is a tennis tournament where every court has a good and bad side. The bad side probably could be facing into the sun. What is a fair way to make sure every player has the good and bad sides an equal number of times?
To solve that problem, I submit using the “Lizard Spock Expansion,” as explained in the Big Bang Theory. This method of playing rock-paper-scissors works with any odd number of symbols. To fairly determine which player gets the good side, consider the seven-player case. The following diagram shows which player gets the good side as shown by the arrow pointing towards the player getting the bad side.
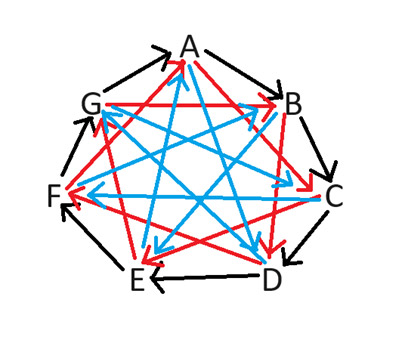
For example, if players B and D played, B would get the good side, because the arrow between them points towards D. It’s not hard to see how I drew the diagram. Arrows always point in a clockwise direction. One needs to draw them for every possible number of gaps from 1 to 3.
However, one doesn’t need to draw such a diagram, but only a ring of letters. Consider both ways to go around the circle in a clockwise manner to get from one player to the other. The way with fewer steps will get the good side. Consider a game between B and F. Going clockwise, it is four steps from B to 4 and three steps from F to B. Since three is less than four, F gets the good side.
The following table shows all possible matchups in a seven-player round robin, including which players get the good and bad sides.
| Round | Good side | Bad side |
|---|---|---|
| 1 | A | B |
| 1 | C | bye |
| 1 | D | G |
| 1 | E | F |
| 2 | A | bye |
| 2 | G | B |
| 2 | C | F |
| 2 | D | E |
| 3 | G | A |
| 3 | F | bye |
| 3 | B | E |
| 3 | C | D |
| 4 | F | A |
| 4 | E | G |
| 4 | D | bye |
| 4 | B | C |
| 5 | E | A |
| 5 | D | F |
| 5 | G | C |
| 5 | B | bye |
| 6 | A | D |
| 6 | C | E |
| 6 | F | B |
| 6 | G | bye |
| 7 | A | C |
| 7 | B | D |
| 7 | E | bye |
| 7 | F | G |
Unfortunately, this side balancing strategy doesn’t work for an even number of players. This is because the two distances are the same around the circle when the two players are on exact opposite sides. If forced, one could use this method for all other matchups, but the players would have to randomize when 180 degrees apart on the circle.
That is as far as I will take this topic for now. I reserve the right to expand on it in a future newsletter. Possible topics for further discussion are matches with three or more players as well as using multiple courts where it is desired to balance how often each player plays on each court.
In closing, I wish you all a happy Hanukkah!


