Rock Paper Scissors Minus One
We continue to take a break from my series on the Camino de Santiago to address the game known as “rock paper scissors minus one.”
The game is shown in episode one of season two of the Squid Game. The show itself is full of interesting game theory and this new game is no exception. I presume the reader already knows the rules of classic version of rock paper scissors.
Here are the rules of rock paper scissors minus one.
- 1. In the first stage of the game, both players, at the same time, play symbols of their choice, one with each hand.
- 2. Both players are given a moment to consider their next move.
- 3. In the second stage of the game, both players, at the same time, pull back one hand, thus playing the symbol on the other hand.
- 4. Rules of classic rock paper scissors determine the winner based on the one remaining symbol by each player.
The following video explains the rules.
While the explanation of the rules was correct and amusing, the advice given was absolutely WRONG! This opinion is based on the assumption that in a tie they would play again, unless there was a winner. Here is the situation in the example shown in the video:
Triangle plays paper and scissors.
Circle plays paper and rock.
At the 1:18 point in the video, the Recruiter says Triangle should play paper because no matter what Circle plays, the game will at least be a tie.
Let’s examine the situation carefully. The following table shows the outcome of all four possible situations from the perspective of the Triangle player.
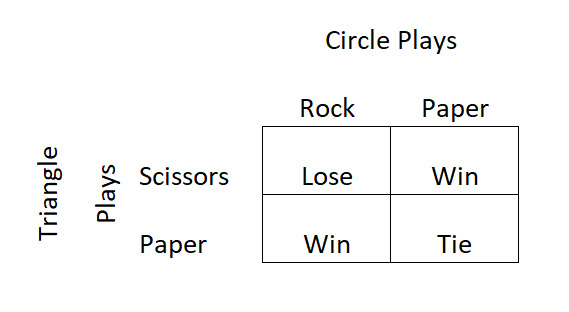
As you can see, from the Triangle’s perspective, there are two wins to win, one way to tie and one way to lose. The reverse is true from the Circle’s perspective, with one way to win, one to tie and two to lose. So, the Triangle is in a position of advantage.
The Recruiter is right in that if Triangle plays paper, then he ensures at least a tie. However, if Circle predicted that thinking, then he could get out of his disadvantageous position by playing paper as well, resulting in a tie.
If Triangle could predict Circle would think that and play Paper, then he could win the game by taking a chance with Scissors. However, if Circle could see that, he would take a chance and play rock, crushing Triangle’s scissors. Then again, if Triangle could predict Circle would play Rock, he would come full circle and play Paper, defeating Circle’s rock. And so it goes, around and around, much like classic Rock Paper Scissors.
The correct strategy for both sides is to randomize! Let’s work it out.
Let:
s = Probability Triangle plays scissors
r = Probability Circle plays rock.
The key with game theory questions like this is to find a probability where your expected win is the same, regardless of what your opponent plays. Thus, it doesn’t help your opponent to crack your strategy.
Let f(s) = Expected win if Triangle plays scissors.
= -rs + s(1-r) + (1-s)r + 0*(1-s)(1-r)
= -rs + s – rs + r – sr
= s + r – 3sr
Next, take the derivative with respect to s and set equal to 0:
f’(s) = 1 – 3r = 0
r = 1/3.
Let f(r) = Expected win if Circle plays rock.
= rs - r(1-s) - (1-r)s + 0*(1-s)(1-r)
= rs–r + rs – s + rs
= -s - r + 3sr
Next, take the derivative with respect to r and set equal to 0:
f’(r) = -1 + 3s = 0
s = 1/3.
Thus, the optimal strategy, contrary to what the Recruiter said is:
- • Triangle should play scissors with probability 1/3 and paper 2/3.
- • Circle should play rock with probability 1/3 and paper 2/3.
If at least one player follows this strategy, the following will be the outcome per game:
- • Triangle wins = 4/9 = 44.44%
- • Tie = 4/9 = 44.44%
- • Circle wins = 1/9 = 11.11%
Counting a win as +1, a tie as 0 and a loss at -1, the expected win by Triangle is 1/3 = 33.3%.
Thank you for reading and I hope you are enjoying season 2 of Squid Game as much as I am!


