Proof the Harmonic Series Diverges

This week’s proof will be that the harmonic series converges. However, before we get to that, I present the usual weekly logic puzzle.

Logic Puzzle

On Monday there are two babies in a hospital nursery, one boy and one girl.

On Tuesday a new baby is added.

On Wednesday a baby is selected at random. It is a boy.

What is the probability the baby born on Tuesday was a boy?.

Proof the Harmonic Series Diverges

The harmonic series is the set of inverses of all integers. In other words, 1 1 , 1 2 , 1 3 , 1 4 , 1 5 ,…, 1 ∞ . A series is said to be divergent if the sum of all it’s members is infinite. This is not obvious in the case of the harmonic series because the members grow infinitely small. However, let me prove the sum is indeed infinite.

Method 1: The Comparison Test

If I can prove another series with equal or lesser members is divergent, then so must the harmonic series.

Harmonic series: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 , 1 7 , 1 8 , 1 9 , 1 10 , 1 11 , 1 12 , 1 13 ,…, 1 ∞ .

Series 2: 1 1 , 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 32 ,…, 1 ∞ .

Series 2 starts with the same two members as the Harmonic series. Then, for every n>=2, it repeats 1 2ⁿ  x  2^n-1times. Note that every member of series 2 is equal or less than that in the Harmonic series. Series 2 can be broken into groups that sum to 1 2ⁿ  X 2^n-1 = 1 2 . Let me illustrate by giving each group a different color:

Series 2: 1 1 , 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 times), 1 64 (32 times) …, 1 ∞

 

1 + ( 1 2  X ∞)= ∞

 

Method 2: Calculus

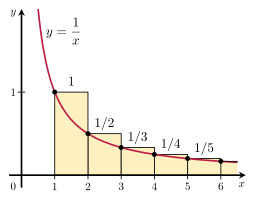
Note the area of the yellow rectangles is greater than the area under the red curve. That area on the red curve is:

∫₁^∞ 1 x dx = ln(x) + c from 1 to ∞ = ln(∞) + c – ln(1) – c = ∞.

Logic Puzzle Solution

Short Answer

There are two possible explanations for what happened. Let's call them X and Y.

X = Boy added on Tuesday and a boy is observed on Wednesday. The probability of this is (1/2)*(2/3) = 2/6 = 1/3.

Y = Girl added on Tuesday and a boy is observed on Wednesday. The probability of this is (1/2)*(1/3) = 1/6.

X+Y = 1/3 + 1/6 = 1/2

The question is asking what is the probability of the two, X is what happened. This would be X/(X+Y) = (1/3)/(1/2) = 2/3.

Long Answer

The Bayesian conditional probability formula says that Prob(A given B) = Prob(A and B)/Prob(B), where prob(x)=probability of any event x. Let's let:

A = Boy added on Tuesday

B = Boy observed on Wednesday

In this case:

Prob(A given B) = Prob(Boy added on Tuesday given boy observed on Wednesday) = Prob(Boy added on Tuesday and boy observed on Wednesday)/Prob(Boy observed on Wednesday).

Given no information about the Tuesday draw, there is a 50% chance of a boy was added on Tuesday. Assuming the Tuesday baby was a boy, there would be a 2/3 chance the baby drawn on Wednesday is a boy.

Likewise, given no information about the Tuesday draw, there is a 50% chance of a girl was added on Tuesday. Assuming the Tuesday baby was a girl, there would be a 1/3 chance the baby drawn on Wednesday is a boy.

The probability a boy was drawn Wednesday equals prob(boy added on Tuesday)*prob(boy drawn Wednesday) + prob(girl added on Tuesday)*prob(boy drawn Wednesday) = (1/2)*(2/3) + (1/2)*(1/3) = 1/2.

The proability a boy was added on Tuesday and a boy drawn on Wednesday = (1/2)*(2/3) = 1/3.

Thus, the answer is (1/3)/(1/2) = 2/3.