Proof of Pythagorean Formula

This week, I will prove the classic Pythagorean formula, which says that in a right triangle the sum of the squares of the sides equals the square of the hypotenuse. The most famous example is the right triangle of sides 3, 4 and 5. Notice 3² + 4² = 5². However, before we get to that, I present the usual weekly logic puzzle.

Logic Puzzle

An absent-minded ancient philosopher forgot to wind up his big clock hanging on the wall in the house. He had no radio, TV, telephone, internet, or any other means for telling time. So, he traveled on foot to his friend's place few miles down the straight desert road. He stayed at his friend's house for the night and when he came back home, he knew how to set his clock.How did he know?

The answer is at the end of the newsletter.

Proof of Pythagorean Formula

Consider the following diagram, which consists of a large square divided into four equal right triangles and a smaller square in the middle. There will be a square in the middle because the sum of the angles of any triangle is 180 degrees. I proved this in the November 13, 2025 newsletter.

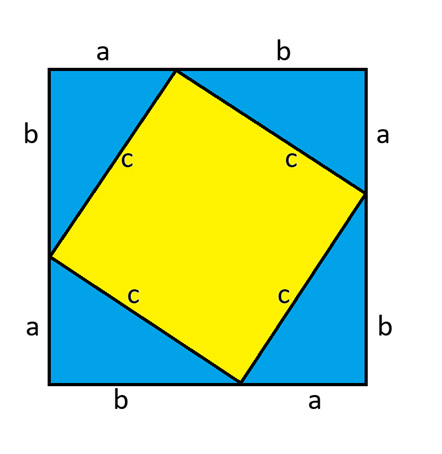
The area of the large square is (a+b)². The area of each triangle is ab 2 . The area of the yellow square in the middle is c². Equating the area of the large square to the sum of the interior parts we get:

(a+b)² = 4 ab 2  + c²

a² + 2ab + b² = 2ab + c²

Subtracting 2ab from both side we get:

a² + b² = c²

Logic Puzzle Solution

1. The professor wound the clock and set it to an arbitrary time.
2. When he gets to his friend’s house, he notes the time of arrival.
3. When he leaves, he notes the time he left as well as calculates the time spent at the friend’s house by subtracting the time he arrived from the time he left.
4. He is careful to walk at the same speed returning as he did going to his friend’s house.
5. When he arrives back at his house, his clock will have advanced the time spent at his friend’s house plus the walking time. He can calculate the walking time by subtracting the time at the friend’s house from the total time. He can then calculate the one-way time by dividing the total walking time by 2.
6. He can then set his clock as the time he left the friend’s house plus one-way walking time.

 

Let’s look at an example.

The incorrect clock is wound and set to 12:00. At the actual time of 8:00, he arrives at his friend’s house. At 1:00, he leaves, noting the five-hour visit. When he returns, he sees his clock is at 8:00. Subtracting the five-hour visit, that means he spent three hours in total walking. That means 1.5 hours each way. If he left at 1:00 and walked for 1.5 hours, it must now be 2:30, which he then sets his clock to.