Inscribed Angle Theorem Proof (part 2)

You may recall last week I started on a proof of the Inscribed Angle Theorem. This week, we finish it. However, before we get to that, I present my usual weekly logic puzzle.

Logic Puzzle

Which of the following statements are true?

1. One of these statements is false.
2. Two of these statements is false.
3. Three of these statements is false.
4. Four of these statements is false.
5. Five of these statements is false.
6. Six of these statements is false.
7. Seven of these statements is false.
8. Eight of these statements is false.
9. Nine of these statements is false.
10. Ten of these statements is false.

 

The answer appears at the bottom of the newsletter.

Inscribed Angle Theorem (part 2)

Let me remind you what the Inscribed Angle Theorem says.

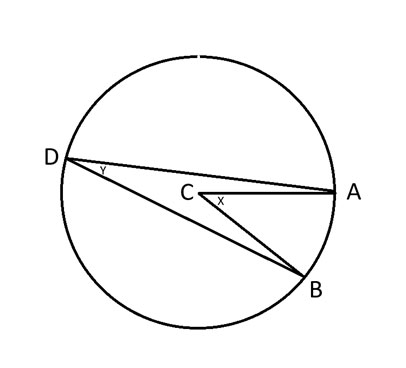
A, B and D = Any three points on the circle.

C = Center of the circle.

x = Angle ACB.

y = Angle ADB.

The inscribed angle theorem says that angle 2y = x.

Last week I showed this to be true in the specific case where AD or BD formed a diameter of the circle. This week I will use that to show the theorem is true for the general case for D.

I’m going to break down all possible locations for D as follows:

Case 1 = AD or BD forms a diameter of the circle (proved last week)

Case 2 = D lies (or is it “lays”?) along the arc on the opposite side of the circle from A and B.

Case 3 = All other

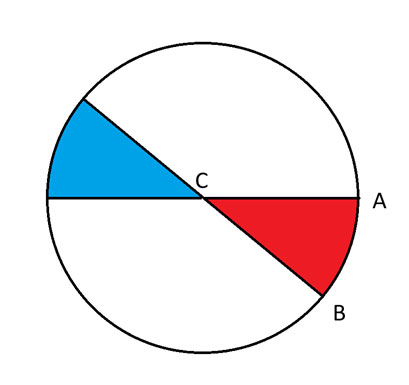
In other words, case 2 will cover the cases where D is along the edge of the circle in the blue region. Case 3 will be other locations outside of that blue slice.

Let’s use the following diagram for discussion.

Let:

x = x1 + x2

y = y1 + y2

z = z1 + z2

We endeavor to prove that x = 2y

I carefully drew a line from D to C, forming a diameter of the circle. Point E is where it intersects the other side of the circle.

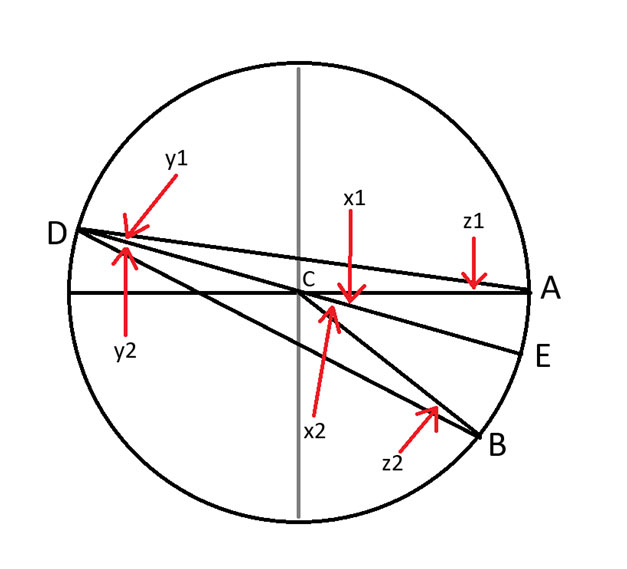
The numbers in the angles should have been subscripted, by my drawing software didn’t allow it.

Consider the triangle ADE.

Since DE forms a diameter, we can use what we proved last week to show 2x1 = 2y1.

Now consider triangle EDB.

By the same logic, 2x₂ = y₂.

Adding these equations:

2x₁+ 2x₂= y₁ + y₂

2(x₁ + x₂) = y₁ + y₂

2x = y

And we’re done with case 2.

Let’s look at case 3.

Here we endeavor to show 2x₁ = y₁.

From case 1:

2x₂ = y₂

2(x₁ + x₂) = y<₁+y₂

Subtracting the upper equation from the lower equation:

2x₁ = y₁

And we have proven case 3.

Logic Puzzle Answer

Only statement 9 is true.

Logic Puzzle Solution

We have ten statements contradicting each other. If you have ten people saying different things either only person is right or none of them are.

Let’s consider the case where all ten statements are false. That would make statement number 10 true. That would make only nine statements false. Thus, a contradiction. There must be a true statement. But which one?

If one statement is true, then nine are false. It is statement number 9 that says that. Thus, only statement 9 is true.