WOO logo

Wizard Recommends

Inscribed Angle Theorem Proof (part 1)

This week we return to my theme of proving a mathematical theorem. The one this week is the Inscribed Angle Theorem. This proof is more involved than usual, so I will break it into two parts, with part 2 next week. However, before we get to that, I present my usual weekly logic puzzle.

Logic Puzzle

In the diagram below, move one coin to form two lines of four coins each.

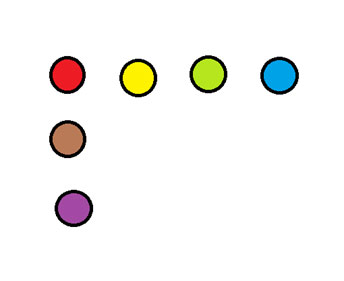
diagram

The answer appears at the bottom of the newsletter.

Inscribed Angle Theorem Proof (part 1)

Before explaining the Inscribed Angle Theorem, let me define some points on a circle in the following diagram.

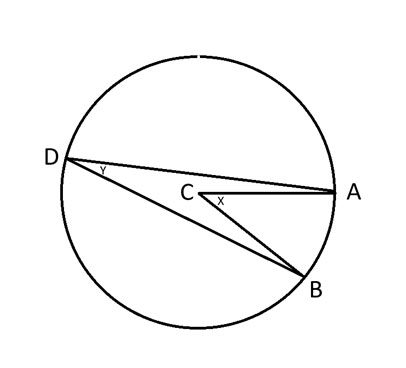
circle

A, B and D = Any three points on the circle.

C = Center of the circle.

x = Angle ACB.

y = Angle ADB.

The inscribed angle theorem says that angle 2y = x.

In this newsletter, I will endeavor to prove it for the specific case where AD or BD form a diameter of the circle. Next week, I will expand on that for the general case of the location of D.

Let’s call the specific case where AD forms a diameter of the circle Case 1. Here is a new diagram for that case.

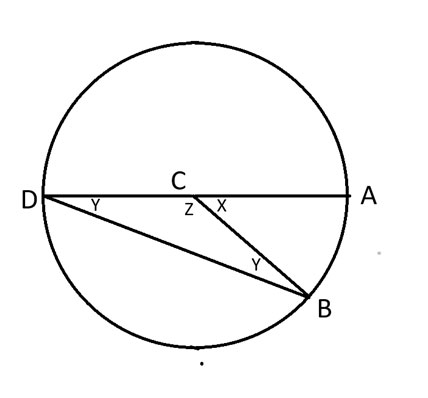
diagram ad

In the diagram above, AD forms a diameter of the circle with C in the center.

We can say x+z = 180 degrees, because they comprise half the total 360 degrees of a circle.

BCD forms an isosceles triangle. Thus, angle CDB = CBD = y.

As proven in my November 13, 2025 newsletter, the sum of the interior angles of a triangle equals 180 degrees. In other words, z + 2y = 180 degrees.

Let’s rewrite both equations:

z = 180 – x

z = 180 – 2y

Let’s equationboth of them, since they both equal z.

180 – x = 180 – 2y

-x = -2y

x = 2y.

So, we have proven the specific case of the Inscribed Angle Theorem where two points on the circle form a diameter. Next week we will build on this to prove it for the general case.

Logic Puzzle Solution

Move the blue coin above the red coin. In the diagram below the numbers show the number of coins in each stack.

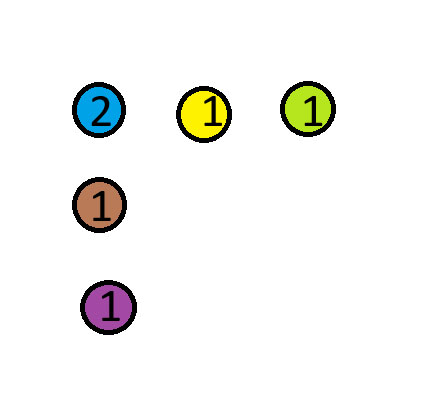
coins

Acknowledgement: I got this puzzle from the Mind Your Decisions YouTube Channel. This one is puzzle #3 in the linked video.