How to Game the Chess Rating Rules

This week we look at a way to game to chess rating formula to improve your rating, without improving your game one bit. Fair warning that it is a small advantage only and mainly of academic interest. However, before that, as usual, I present our weekly logic puzzle.

Logic Puzzle

There are 50 people in a line, numbered 1 to 50 sequentially. The first person in line is number 1. Each person either always tells the truth or always lies. Everyone knows the truthfulness of everyone else.

All even-numbered people say, "Everyone in front of me is a liar."

All odd-numbered people say, "Everyone behind me is a liar."

Who is telling the truth?

How to Game the Chess Rating Rules

The most common chess-rating system, as far as I know, is the Elo rating system. It is named after Arphad Elo. The same system is also used in other games and sports.

Basically, the way it works is a formula determines the probability of any given player winning a game according to the ratings of both players. The winning player will gain points in proportion to his probability of losing. Likewise, the losing player will gain points in proportion to his probability of winning. One point is awarded for a win, 0.5 for a draw and 0 for a tie.

The system is based on the assumption, which I agree with, that a player’s performance can be modeled after a random number drawn on the bell curve, with the player’s rating as the mean. The player who gets the higher number wins.

The way the probability of winning is determined is as follows:

Let r1 = rating of player 1.

Let r2 = rating of player 2.

p = Probability player 1 wins.

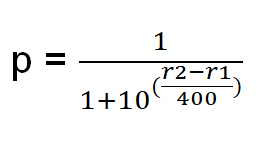
Let’s look at an example. Let r1=1900 and r2=2000.

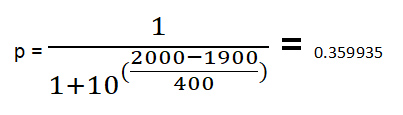
Assuming 1 point is given for a win and 0 for a loss, then the increase in rating is 32*(actual points – probability of winning).

In our example above, if player 1 loses, as he is predicted to do, then his rating drops by 11.52 points and the rating of player 2 goes up by the same number. If player 1 wins, his rating goes up by 20.48 points and player 2 goes down by the same number.

The Elo scheme is based on a standard deviation in performance, as modeled by the random number method described above, as 200. This I assume to be true. However, the probability of winning formula, from which Elo tables are based, is not consistent with such a standard deviation, except if the difference in ratings is 0 or 189.

The correct probabilitythat the player with the r1 rating wins is:

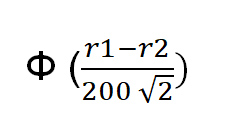
Where the function Φ(x) = the probability that a random standard normal variable is less than x. In Excel, the correct formula is norm.s.dist((r1-r2)/(200*sqrt(2)),1).

Let’s look at a case where the difference in ratings is 100. Let’s make player 1 the underdog. The Elo formula suggests player 1 has a 35.99% chance of winning. However, his actual probability, based on a standard deviation in performance of 200, is 36.18%. In other words, player 1 taking the game is a good bet and a bad bet for player 2. I show the expected gain in rating of player 1 and expected loss of player 2 is 0.06 points.

Next let’s look at difference in ratings of 300, where player 1 is the underdog. Here the Elo formula gives player 1 a 15.10% chance of winning, when I show it is 14.44%. That makes taking the game a bad bet for player 1 and a good one for player 2. The expected loss for player 1 is 0.21 points as well as the expected gain for player 2.

That math behind the actual probabilities is based on the Gaussian curve and more involved than I care to get into for this newsletter.

The bottom line is if the difference in ratings is over 189, taking the game is a good bet for the favorite. Likewise, if it is less than 189, taking the game is a good bet for the underdog.

However, the bias is rather small. I would not accept or decline games based on this information. Rather, I think you should take any game for the love of chess.

Further reading: Wikipeida article on the Elo rating system.

Logic Puzzle Answer

People 2 and 49 are the only ones telling the truth.

Logic Puzzle Solution

Let’s start with person 1. If he is telling the truth, then everyone else is lying. However, person 3 says everyone from 4 to 50 is lying. If that is true, then person 3 is truthful. However, person 1 says he is lying. This leads to a contradiction. Thus person 1 must be lying.

Person 2 says only that person 1 is lying. This makes person 2 truthful.

Every even-numbered person from 4 to 50 says person 2 is lying. That makes them all liars.

Person 49 says person 50 is lying, which is true. That makes person 49 truthful.

Every odd numbered person from 3 to 47 says person 49 is lying. That makes them all liars.

Thus, the only people telling the truth are numbers 2 and 49.