WOO logo

Wizard Recommends

Euler’s Identity

This week we take on a big challenge, proving Euler’s Identity. If you forgot, it is perhaps the most beautiful identity in mathematics: eπi+1 = 0. I love this identity so much, it’s on my business card and I may even get a tattoo of it. However, before we get to that, I present the usual weekly logic puzzle.

Logic Puzzle

You have four chains consisting of three links each. How can you join them all together to make a circular loop of all 12 links with cutting only three links?

Proving Euler’s Identity

One of the most famous equations in mathematics is Euler’s Identity, which says eπi+1 = 0. What’s amazing about it is it combines the five most important numbers in math: 0, 1, e, π and i.

My solution requires knowing the formula for a Taylor expansion. As a reminder, it is:

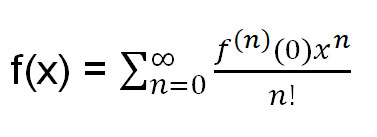
formula

Where f(n) (0) = the nth derivative of f(x) evaluated at 0.

I personally find the equation one of the most amazing and beautiful in all mathematics. To me, it is evidence there is something divine about math.

That said, here are three Taylor expansions to common functions we will need:

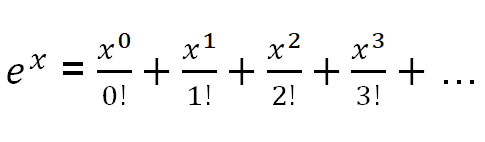
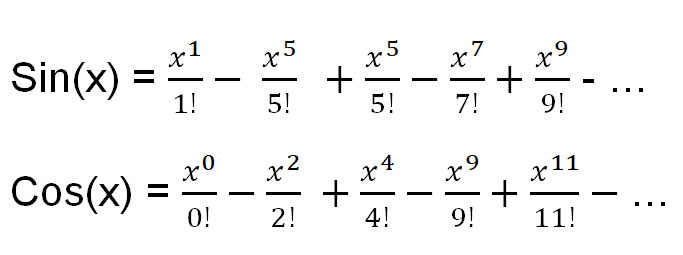
expansions
expansions

Let’s use the Taylor expansion of ex to find eπi.

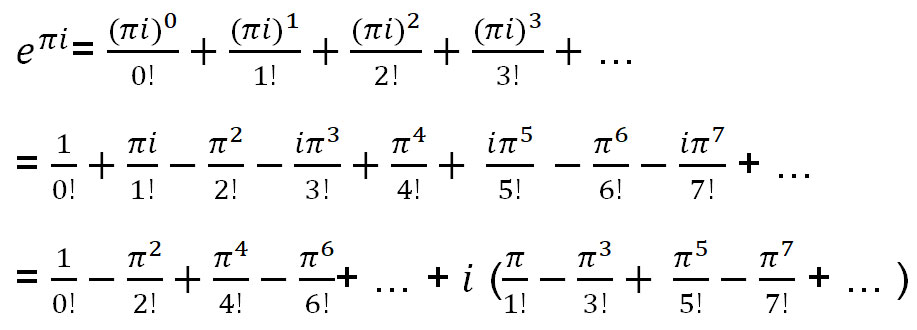
expansions

The equation above can be expressed as functions of sin(x) and cos(x):

= cos(π)+i ×sin⁡(π)

= -1 + i ×0

= -1

So, we have eπi= -1. This can be rearranged into the usual format:

eπi+1 = 0

Logic Puzzle Solution

  1. Take one of the four chains and open and separate all three links. Call the other three chains 1, 2, and 3.
  2. Use one link to combine chains 1 and 2, creating a seven-link chain.
  3. Use another link to combine the seven-link chain from step 2 to chain 3, creating an 11-link chain.
  4. Use the last link to join the two ends of the 11-link chain from step 3 to create a 12-link circle.