On this page
Legend Behind Pai Gow
Introduction
Pai gow (tiles) is perhaps the oldest casino game. The name roughly translates to "make nine." In fact, the concept of scoring by the ones digit only, as in baccarat, likely stems from pai gow.
Of all the casino games, there can be little debate that pai gow is the hardest to learn. Before playing the game, one should learn the ranking of 16 pairs of tiles. To the westerner, or anybody not steeped in Chinese mythology, this ranking will likely seem arbitrary and thus difficult to memorize. However, there is a legend behind the game, and acquainting oneself with that legend can aid in understanding the order of the pairs.
On December 30, 2011, I met a very nice Caucasian gentleman by the name of Colonel Rob Patton at the pai gow table at the Paris casino in Las Vegas. He mentioned that he had been playing the game for about 25 years. This took me quite by surprise. When I started to play the game around 2001, there was almost never another pale-faced player at the table. Now I would say non-Asians make up about 20% of the players.
In the mid Eighties, I would have been shocked to see any non-Asians playing. Based on early literature, the few Caucasian players you might have found were likely mathematicians like Michael Musante, John M. Gwynn Jr., or Bill Zender. To this day, white players are still often made to feel a bit unwelcome at pai gow tables. The attitude that "whitey" can be unlucky is still prevalent in Macau and Australia.
Rob said his efforts to learn the game were not easy, due to Asian dealers not having the ability or inclination to explain the game in English. One day, though, he found a Caucasian dealer at Caesars in Lake Tahoe who was very helpful. In his efforts to explain the tile rankings, he told Rob the Chinese legend of the creation of the universe to help with the explanation. Here it is:
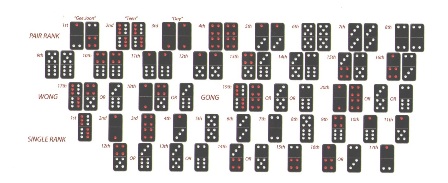
Part 1 - The Supreme Pair
| Supreme Creator (Gee Joon): Chinese name of the Supreme Creator, which came before anything else. |  |
Part 2 - The Civilian Pairs
| Heaven (Teen): The Creator first made the stars to fill the void of space. |  |
| Earth (Day): Then he made the earth. |  |
| Man (Yun): Then he created man to live on the earth. |  |
| Goose (Gor): Then he created geese for man to eat. |  |
| Plum flower (Mooy): Then he made flowers to give the earth beauty. |  |
| Long (Chong): Then he made long robes so man could clothe himself. |  |
| Board (Bon): Then he made boards to make benches for man to sit on. |  |
| Hatchet (Foo): Then he made hatchets for man to chop wood. |  |
| Partition (Ping): As man's family grew, he made partitions to separate rooms in man's house. |  |
| Long Leg Seven (Tit): Man's seventh child had long legs. |  |
| Big Head Six (Look): Man's sixth child had a big head. |  |
Part 3 - The Military Pairs
Finally come the mixed pairs, which represent the military. The greater the number of dots, the higher the rank.
| Nine (Gow) |  |
| Eight (Bot) |  |
| Seven (Chit) |  |
| Five (Ng) |  |
Rank of the 2-4 Gee Tile
Some casino rule books state the value of the 2-4 tile is above the two fives, while others rank it last with the 1-2 tile. In my own explanation of the rules, I rank it last. So, why the discrepancy? According to John Gwynn, who quotes Michael Musante, in his article 'A Detailed Study of Pai Gow,' (page 308), published in Finding the Edge, there is an unwritten rule that the 2-4 tile is ranked just above the five-point tiles (1-4 and 2-3), except if it is used to count as three points, in which case it is ranked last, with the 1-2 tile. This demotion only makes a difference when the Gee tile is combined with either five-point tile (1-4 or 2-3). In this case it is treated as three points, demoting it below the rank of the five-point tile. So, for all intents and purposes, both Gee tiles should be and effectively are ranked last.
If we assume that Gwynn and Mustante are right, and I wouldn't trust anybody more than them, then I would claim that the Venetian rules are in error, which imply the 2-4 tile is always ranked higher than the five-point tiles. However, this would only come into effect if the banker had the 1-2 tile and a 5-point tile, and the player had the 2-4 tile and the other 5-point tile. According to the rule booklet, the Venetian would score it as a win for the player. However, both hands should be equally ranked, which would be a win for the banker. The odds of this are 1 in 107,880.
Chinese Dice

Finally, Rob addressed a question I have wondered about for years: Why do dice in all the Chinese games, namely pai gow, pai gow poker, baccarat, and sic bo, paint the one and four red but all the other numbers black? His answer follows.
Each tile pattern in the Chinese domino set is made up of the outcome of a throw of two six-sided dice. There are therefore 21 unique patterns (6+5+4+3+2+1).
Using the same coloring scheme of the traditional Chinese dice, every half domino with 1 or 4 spots has those dots colored red, (for example, the 4-5 domino has four red spots and five white spots). The only exception is the pair of 6-6 tiles. Half of the spots on the 6-6 domino are colored red to make them stand out as the top ranking Civilian tiles. In Pai Gow, dot color plays no role in the play of the game; it is only to visually make the tiles traditional.
The Chinese custom of painting the 4-spot red is said to have originated when an Emperor playing sugoruku (Japanese Backgammon) with his queen was about to lose and desperately needed fours to win the game. He cried out, threw the dice and they came up accordingly. He was so glad that he ordered that fours be painted red from then on.
The emperor is said to have been Lo Ling Wong who reigned under the title Chong Tsung (AD 684 - 701) during the Tang dynasty. Whether this story is true is questionable, and it has been suggested that the 4-spot is painted red because dice were imported from India where red fours are also traditional. The reason why the 1-spot is large and painted red is not clear. It is said the stark combination of black and white would be unlucky, red being considered very lucky in China. Another possibility is that it counters and balances the die, compensating for the opposite 6-spot indentations.