On this page
Mega Millions
On this page
Introduction
The Mega Millions is a multi-state lottery known for very large jackpots. It started in 1996 known as "The Big Game." Since then it changed names to "The Big Game Mega Millions" and finally just "Mega Millions." It has also gone through a number of rule changes along the way. This page addresses the rules effective after a rule change on October 28, 2017.
Buy Lottery Tickets Online
Rules
The rules were changed on October 28, 2017, increasing the cost from $1 to $2, making the jackpot harder to hit, with the intention of growing bigger jackpots. I suspect the rule changes were a response to competition from the Powerball Lottery. The rules of both lotteries are now very similar.
- The cost of a ticket is $2.
- The player shall pick five distinct numbers from 1 to 70, as well as one "Power Ball" from 1 to 25.
- Every Tuesday and Friday, at 11:00 PM eastern time, the lottery shall draw five white balls numbered 1 to 70 and one red Power Ball from 1 to 25.
- The player shall win according to how many of his picks match the ball draw, as shown in the table below.
Pay Table
White
Balls
MatchPower
Ball
MatchesWin 5 Yes Jackpot 5 No $1,000,000 4 Yes $10,000 4 No $500 3 Yes $200 3 No $10 2 Yes $10 1 Yes $4 0 Yes $2 0 to 2 No $0 - The player may also pay an extra $1 to enable the Megaplier multiplier, except in California. If the player invokes the Megaplier option, then any prizes other than the jackpot will be multiplied by 2 to 5, according to the probabilities in the table below.
Megaplier
Multiplier Weight Probability 5 1 0.066667 4 3 0.200000 3 6 0.400000 2 5 0.333333 Total 15 1.000000 - Yet another option allows the player to buy two tickets for $3, but both will only qualify for the jackpot only.
- The advertised jackpot amounts are paid as a 30-year annuity, with the first payment payable immediately at 1.5051435% of the total amount payable. Future payments will go up by 5% per year, compounded annually.
- In lieu of the annuity, the player may opt for a lump sum, which will be about 62.5% of face value.
- The pay table is different for California, because all prizes must be paid on a pari-mutual basis in that state.
- As with any lottery with a big progressive, if more than one player wins, then the jackpot will be split evenly among all winners.
- As with any lottery with large prizes, if a very frequently chosen set of numbers hits, like the Lost numbers of 4-8-15-16-23-42, then prizes, including fixed ones, may have to be reduced.
- The jackpot is paid out as a 30-year annuity, with payments once a year, starting immediately. Each payment is 5% greater than the previous one. For the total payments to equal the amount won, the first payment will be 1.50514% of the total win. The player may also choose a lump sum option. At the time of this writing (Oct. 16, 2018) the lump sum option on a $654 jackpot was $372 million, or 56.88% of the total amount. I believe this ratio fluctuates.
Analysis
The following table shows the probability and expected return for all possible outcomes, assuming the player did not invoke the Megaplier option and a jackpot of $40 million. The return column is the product of the win, probability and 0.5. The reason for dividing by 2 is the cost of a ticket is $2. This table does not consider the factors of taxes, the annuity on the jackpot, and jackpot sharing. Some analysis follows the table.
Mega Millions Return Table — No Megaplier
| White Balls Match |
Red Ball Matches |
Combinations | Probability | Win | Return |
|---|---|---|---|---|---|
| 5 | Yes | 1 | 1 in 302575350 | $40,000,000 | 0.066099 |
| 5 | No | 24 | 1 in 12607306 | $1,000,000 | 0.039660 |
| 4 | Yes | 325 | 1 in 931001 | $10,000 | 0.005371 |
| 4 | No | 7,800 | 1 in 38792 | $500 | 0.006445 |
| 3 | Yes | 20,800 | 1 in 14547 | $200 | 0.006874 |
| 3 | No | 499,200 | 1 in 606 | $10 | 0.008249 |
| 2 | Yes | 436,800 | 1 in 693 | $10 | 0.007218 |
| 1 | Yes | 3,385,200 | 1 in 89 | $4 | 0.022376 |
| 0 | Yes | 8,259,888 | 1 in 37 | $2 | 0.027299 |
| 0 to 2 | No | 289,965,312 | 95.83% | $0 | 0.000000 |
| Total | 302,575,350 | 0.189590 |
The lower right cell of the table above shows the player can expect to get back 18.96% of his money at a jackpot of $40 million. The rate of return goes up by 16.52% for every additional $100 million in the jackpot. The break-even point, where the expected return would be 100% is $530,420,124*. The probability of any win is 4.17%.
* Does not consider the annuity, taxes, or jackpot sharing.
Megaplier Analysis
The following table shows the probability for each multiplier. The lower right cell shows the average multiplier for the Megaplier is 3.00.
Megaplier
| Multiplier | Weight | Probability | |
|---|---|---|---|
| 5 | 1 | 0.066667 | 0.333333 |
| 4 | 3 | 0.200000 | 0.800000 |
| 3 | 6 | 0.400000 | 1.200000 |
| 2 | 5 | 0.333333 | 0.666667 |
| Total | 15 | 1.000000 | 3.000000 |
The following table shows the probability and expected return for all possible outcomes, assuming the player did invoke the Megaplier option and a jackpot of $40 million. The win column is the base win, before applying the Megaplier. The return column is the product of the win, probability, average Megaplier, and 1/3 The reason for dividing by 3 is the cost of a ticket is $3 with the Megaplier. This table does not consider the factors of taxes, the annuity on the jackpot, and jackpot sharing. Some analysis follows the table.
Mega Millions Return Table — With Megaplier
| White Balls Match |
Red Ball Matches |
Combinations | Probability | Win | Return |
|---|---|---|---|---|---|
| 5 | Yes | 1 | 1 in 302575350 | $40,000,000 | 0.044066 |
| 5 | No | 24 | 1 in 12607306 | $3,000,000 | 0.079319 |
| 4 | Yes | 325 | 1 in 931001 | $30,000 | 0.010741 |
| 4 | No | 7,800 | 1 in 38792 | $1,500 | 0.012889 |
| 3 | Yes | 20,800 | 1 in 14547 | $600 | 0.013749 |
| 3 | No | 499,200 | 1 in 606 | $30 | 0.016498 |
| 2 | Yes | 436,800 | 1 in 693 | $30 | 0.014436 |
| 1 | Yes | 3,385,200 | 1 in 89 | $12 | 0.044752 |
| 0 | Yes | 8,259,888 | 1 in 37 | $6 | 0.054597 |
| 0 to 2 | No | 289,965,312 | 95.83% | $- | 0.000000 |
| Total | 302,575,350 | 0.291048 |
The lower right cell of the table above shows the player can expect to get back 29.10% of his money at a jackpot of $40 million. The rate of return goes up by 11.02% for every additional $100 million in the jackpot with the Megaplier option. Before considering the annuity, taxes, and jackpot sharing, the break-even point, where the expected return would be 100% is $224,191,728.
Just the Jackpot Analysis
If the player invokes the "Just the Jackpot" option, the expected return, before considering taxes, the annuity, or jackpot sharing, at the meter reseed value of $40 million is 8.81%. For every additional $100 million in the jackpot, the expected return goes up by 22.03%.
Jackpot Competition
The larger the jackpot gets, the more competition from other players it induces. It is actually a better value to buy tickets at a jackpot of 400 million than a billion, because the jackpot is more likely to get chopped multiple ways when the jackpot gets in that high.
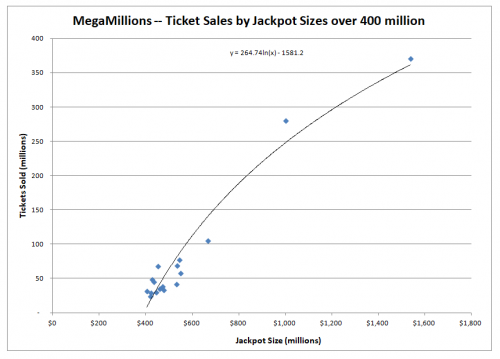
To be specific, I find an exponential relationship between jackpot size and tickets sold when the jackpot is 400 million or less. The following graph plots ticket sales (vertical axis) by jackpot size (horizontal axis).
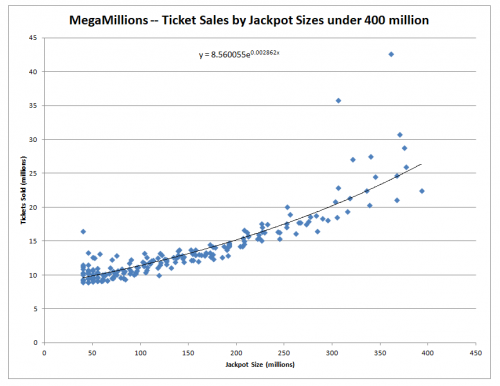
For jackpots over 400 million there is not much data, especially for jackpots close to a billion, as the following graph will show. The black line shows a logarithmic fit between the data points.
I put these least-squares regression curves into my Lottery Jackpot Ticket Sales Calculator. This would be useful to see how many other people you're likely to split a jackpot with according to the jackpot size. There are also Internet sports book that take bets on whether or not a jackpot will be hit.
Other Factors
So far all my analysis has been before making any adjustments for the annuity, taxes, and jackpot sharing. However, let's consider those things.
The most complicated part of this value dilution is jackpot chopping. The following table shows by jackpot size (in million) the estimated number of tickets sold, probability of at least one winner, expected share of the jackpot per winner, and the expected jackpot after any chopping.
Jackpot Chopping
| Jackpot (in Millions) |
Expected Tickets Sold (in Millions) |
Probability Win |
Jackpot Share per Winner |
Expected Jackpot after Chopping |
|---|---|---|---|---|
| $300 | 22.2 | 7.3% | 96.4% | $289 |
| $400 | 36.1 | 11.9% | 94.3% | $377 |
| $500 | 54.9 | 18.1% | 91.5% | $457 |
| $600 | 78.7 | 26.0% | 88.0% | $528 |
| $700 | 107.7 | 35.6% | 84.1% | $589 |
| $800 | 141.8 | 46.9% | 79.8% | $639 |
| $900 | 180.9 | 59.8% | 75.3% | $677 |
| $1,000 | 225.2 | 74.4% | 70.5% | $705 |
| $1,100 | 274.6 | 90.7% | 65.7% | $723 |
| $1,200 | 329.1 | 108.8% | 61.0% | $732 |
| $1,300 | 388.6 | 128.4% | 56.3% | $732 |
| $1,400 | 453.3 | 149.8% | 51.8% | $726 |
| $1,500 | 523.1 | 172.9% | 47.6% | $714 |
| $1,600 | 597.9 | 197.6% | 43.6% | $697 |
| $1,700 | 677.9 | 224.0% | 39.9% | $678 |
| $1,800 | 763.0 | 252.2% | 36.5% | $656 |
| $1,900 | 853.1 | 282.0% | 33.4% | $634 |
| $2,000 | 948.4 | 313.4% | 30.5% | $610 |
Note that the right column in the table above is maximized at $732 million for a jackpot size of 1.3 billion. The closer estimate of the maximum jackpot size after chopping is $1.255 billion. Beyond that, the value goes down because of the induced demand for tickets and thus chopping the jackpot with more winners. In case anyone is wondering, I use parabolic regression to estimate ticket sales for jackpots over $300 million.
The annuity factor is easy. The winner can take the annuity (as explained in the rules section above) or a lump sum equal to some percentage of the jackpot amount. As of Oct. 16, 2018, this percentage was 56.88%. Everybody seems to take the lump sum option. By the way, ignoring all factors besides the interest rate, the time value of the win is greater taking the lump sum option at an interest rate of over 3.40%, otherwise take the lump sum. At the time of this writing (Oct 16, 2018), the 20-year Treasury Bill rate was 3.27%. To keep the math easy, let's assume the winner takes the lump sum option.
Taxes are also pretty easy. At the time of this writing the maximum federal income tax rate was 37%. State taxes vary quite a bit, but let's assume 8% for state and local taxes. That means that the winner will lose 45% to taxes.
Let's use a jackpot size of one billion, for the sake of example. After jackpot sharing, the lump sum, and taxes, you'll be left with $220.6 million. The probability of winning is 1 in 302,575,350. At jackpots this large, the player should take the Jackpot Only option, at a cost of $1.50 per ticket. This makes the value of a ticket $220.6 million / 302,575,350 = 72.9 ¢. Considering the cost of a ticket is $1.50, the expected return is $0.729/ $1.50 = 48.6%. That means a house edge of 51.4%. At the maximum jackpot value of 1.255 billion, the expected return is 52.7%. That is as good as it gets. So, no, the Mega Millions never goes positive. In fact, it never even gets close.
Strategy
 There are three ways to play, as follows:
There are three ways to play, as follows:
- Normal tickets at $2 each.
- Tickets with the Megaplier at $3 each
- "Just the Jackpot" tickets at two for $3.
Again, ignoring taxes, the annuity, and jackpot sharing, the optimal strategy is to invoke the Megaplier option at jackpots under $224,191,728. At jackpots over this amount, the player should buy "jackpot only" tickets. Interestingly, at a jackpot of exactly $224,191,728, the expected return is the same for all three options at 49.40%.
I hate to have to say this, but I've been asked about buying the Megaplier with "jackpot only" tickets. The answer is NO! There are no fixed wins to multiply with "jackpot only" tickets, so you would be multiplying nothing. I would hope they don't even allow this option as it would truly be taking advantage.
Considering the effects of taxes, jackpot sharing, and the annuity, my advice is to buy the Megaplier at any jackpot amount and never invoke the Jackpot only option. The three factors mentioned significantly reduce the value of the jackpot.
Conclusion
Mathematically speaking, the Mega Millions is an awful bet. After considering the Lottery's cut, jackpot sharing, the annuity, and taxes, the expected return never gets much above 40%. I find the decision to buy lottery tickets to be entirely irrational, and I have yet to understand why people queue up to throw their money away.
Lotteries
Games
Related Reading
- Lottery — General page.
- Buy Lotto Online in 2024
- Are Lottery Players Smart? - Do the US states with better lottery returns tend to have a greater loss per resident than the states in which the lotteries return more poorly?
- COVID and the Lottery
- The Lottery Sucks - A Comprehensive Lottery Report
- The Lottery (Still) Sucks!
- Former Ask the Wizard questions about the lottery
Calculators
- Powerball calculator — Calculate for odds for the Powerball, or any lottery with five "white balls" and one "Power Ball."
- Mega Millions calculator — Calculate for odds for the Mega Millions, or any lottery with five "white balls" and one "Mega Ball."
- Pick Six calculator — Calculate for odds for any "pick six" game.
- SuperLotto Plus — California Lottery game.
- Lottery Jackpot Ticket Sales Calculator — Estimate ticket sales and probability of a winner for any jackpot size for the Power Ball and MegaMillions.
External Links
- Big Week for the Lotteries 29 Oct-2018, 2 Huge jackpots are won.
- Mega Millions -Official web site.
- Wikipedia.
- LottoReport.com - Information about historical ticket sales and jackpot sizes.