On this page
Chemin de Fer
Introduction
Chemin de Fer is an antiquated precursor of modern-day baccarat. It would probably not merit much discussion as an extinct game, except for it was much loved by James Bond and I get asked from time to time what exactly Bond was playing. I believe the game finally went the way of the dodo bird in the 1990's. Still it deserves a proud chapter in gambling history and I am happy to help write it.
Rules
To avoid confusion, when addressing the hands of Player and Banker, I will use capital letters and usually say Player Hand or Banker Hand. When referring to a human player or banker, I will use lower case. First I will go over the scoring rules, which are the same as in baccarat and then go over the procedural rules. If you are already familiar with baccarat, you may skip the scoring rules.
Sources differ on some of the rules. I will restrict my analysis to two sources. Other sources seems to copy from one of these sources or other.
- Scarne's New Complete Guide to Gambling (copyright 1974) by John Scarne.
- Casino Royale (copyright 1953) by Ian Fleming.
The Scarne scoring rules are as follows.
- Six (Fleming) or eight (Scarne) decks are used.
- Cards are given point values as follows: Ace = 1, 2-9 = pip value, 10 and face cards = 0.
- There are two hands, known as the Player and Banker.
- After all bets are down, the dealer gives two cards face down to both the Player and Banker hands.
- The way to arrive at the points per hand is to take the total points of each individual card in the hand. If the sum is more than 9, then drop the first digit. For example, if either hand had a 9 and 7, then you would drop the 1 from the total of 16, for a 6-point hand.
- The hand with the greater number of points shall win.
- If either two-card hand has 8 or 9 points, then neither side may draw more cards.
- Otherwise, the player acting on behalf of the Player Hand shall act as follows, based on the point value of that hand.
- 0 to 4 points — Draw
- 5 point — Player has option to Draw or stand.
- 6 or 7 points — Stand
- If the Player Draws, then that third card shall be dealt face up.
- If the no third card was dealt to the Player hand, then the Banker hand shall act as follows, based on the point value of the Banker hand.
- 0 to 5 points — Draw
- 6 or 7 points — Stand
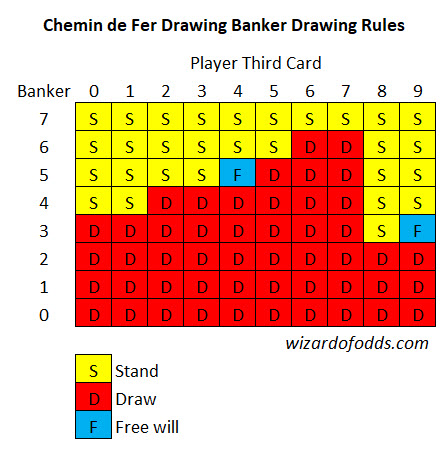
- If a third card is drawn to the Player hand, then use the Banker shall make his decision to Draw or Stand, according to the point value of his two-card hand and the card drawn to the Player hand, as shown in the table below.
- The final point values of the Player and Banker hands are compared. If the Player hand wins, wagers are paid even money. A tie is a push. If the Banker hand wins, wagers lose.
Where the Fleming rules are different is that both sides had free will, barring either side having a natural. However, Fleming seems to indicate that there was a fairly rigid way the game was played, where protocal dictated how to play most hands, leaving few up to free will.
The procedural rules are as follows.
- Unlike baccarat, chemin de fer is a player-banked game.
- The role of the casino is to deal the cards and officiate the game, not to honor bets.
- One player shall be designated to play the Banker Hand and honor all bets on the Player Hand.
- If the Banker Hand won or tied the previous round, the same person may continue to act as the Banker, as long as he is willing to bet the same amount as the previous hand, at least. The alternative choice is to relinquish the shoe.
- If the Banker Hand lost the previous hand, then the player who acted as banker must reliquish the shoe. The next player at the table, going counter-clockwise, has the option to be the banker as long as he is willing to bet at least the same amount as on the previous hand by the previous banker.
- If nobody is willing to bet the requisite amount on the Banker Hand, then the option to act as banker goes to the player willing to bet the most. If there is a tie, the option goes to the player closest to the previous banker, going counter-clockwise around the table.
- Regardless of who is banking and why, the banker has the option to increase the amount he is will to bet, up to two times the amount bet the previous hand.
- Once a banker and maximum bet on the Banker Hand has been established, bets on the Player Hand may be made.
- Any player who is willing to wager the full amount the banker bet has the first priority to do so.
- If more than one player is willing to wager the maximum amount, then the first option shall go to a player who bet the maximum amount on the previous hand and lost. This is known as "suive," which means "follow" in French.
- Otherwise, the option to make a maximum wager is offered around the table, starting with the player to the right of the banker and going counter-clockwise.
- If nobody invokes the option to wager the full banker's risk amount, then the player to the banker's right may wager as much as he wishes, up to the banker's bet.
- Betting continues around the table, going counter-clockwise, until bets on the Player Hand have equaled the Banker bet.
- Once all wagering has been concluded, two cards shall be dealt to both the Player and Banker hands, face down.
- The player wagering the most money on the Player Hand shall get the cards and have any decision-making authority.
- If the two-card Player Hand has eight or nine points, then it should be revealed immediately.
- If the player acting on the Player Hand reveals an eight- or nine-point hand (known as a "natural"), then the Banker Hand shall also be immediately revealed, as neither side may draw.
- Otherwise, after the player acting on the Player Hand has made a stand or draw decision, the Banker shall reveal his two cards.
- If that two-card Banker Hand is a total of eight or nine points, then no third card will be drawn to the Player Hand, because no further cards may be dealt if either side has a two-card hand of 8 or 9 points.
- Otherwise, if player acting on the Player Hand, drew a card, it shall be dealt to him, face up.
- After the player acting on the Player Hand has acted, assuming neither side had a natural 8 or 9 point hand, then the player acting as banker shall have his turn.
- If the Player Hand did not draw a third card, then the Banker shall draw with five or less points and stand on six or seven points.
- Otherwise, if the Player hand did draw a third card, then the Banker hand shall use the table in the Scoring Rules above to determine his action, according to the total points in the two-card Banker Hand and the third card drawn to the Player Hand.
- The hands shall be scored and adjudicated by casino staff.
- According to Scarne, if the Banker Hand won, then the house shall collect a commission, typically 5% of total Player Bets, which the banker must pay. According to Fleming, a "tiny percentage" was charged from each bet. Here are his exact words from Casino Royale (which was based on chemin de fer in the book), "From each bet the Casino takes a tiny percentage, the cagnotte, but it is usual at a big game for the banker to subscribe this himself either in a prearranged lump or by contributions at the end of each hand, so that the amount of the bank's stake can always be a round figure. Le Chiffre had chosen the second course."
Scarne Rules Analysis
Between three free will situations in chemin de fer, there are 2*2*2 = 8 sets of combinations of outcomes on a winning Player Hand, Banker Hand, and a tie. The following table shows those combinations for all eight ways the two sides might play their free will hands.
Full Game Combinations by Strategy
| Player 5 |
Banker 3 vs. 9 |
Banker 5 vs. 4 |
Player | Banker | Tie |
|---|---|---|---|---|---|
| Stand | Stand | Stand | 2,229,630,111,780,860 | 2,306,941,760,323,580 | 461,826,403,398,912 |
| Stand | Stand | Draw | 2,230,267,491,565,560 | 2,307,485,872,054,270 | 460,644,911,883,520 |
| Stand | Draw | Stand | 2,230,806,098,022,400 | 2,306,943,230,140,410 | 460,648,947,340,544 |
| Stand | Draw | Draw | 2,231,443,477,807,100 | 2,307,487,341,871,100 | 459,467,455,825,152 |
| Draw | Stand | Stand | 2,230,565,660,708,860 | 2,290,372,874,305,530 | 477,459,740,488,960 |
| Draw | Stand | Draw | 2,230,944,481,550,330 | 2,290,916,986,036,220 | 476,536,807,916,800 |
| Draw | Draw | Stand | 2,230,139,461,750,780 | 2,291,708,454,707,200 | 476,550,359,045,376 |
| Draw | Draw | Draw | 2,230,518,282,592,250 | 2,292,252,566,437,880 | 475,627,426,473,216 |
The next table takes the combinations of the three possible outcomes in the table above and converts them to probabilities.
Full Game Probabilities by Strategy
| Player 5 |
Banker 3 vs. 9 |
Banker 5 vs. 4 |
Player | Banker | Tie |
|---|---|---|---|---|---|
| Stand | Stand | Stand | 0.446069 | 0.461536 | 0.092395 |
| Stand | Stand | Draw | 0.446196 | 0.461645 | 0.092159 |
| Stand | Draw | Stand | 0.446304 | 0.461536 | 0.092159 |
| Stand | Draw | Draw | 0.446432 | 0.461645 | 0.091923 |
| Draw | Stand | Stand | 0.446256 | 0.458221 | 0.095523 |
| Draw | Stand | Draw | 0.446332 | 0.458330 | 0.095338 |
| Draw | Draw | Stand | 0.446171 | 0.458489 | 0.095341 |
| Draw | Draw | Draw | 0.446247 | 0.458597 | 0.095156 |
The next table shows the expected value of bets on both the Player Hand and Banker Hand. The expected value of the Banker Hand assumes a 5% commission paid on wins.
Full Game Expected Values by Strategy
| Player 5 |
Banker 3 vs. 9 |
Banker 5 vs. 4 |
Player | Banker |
|---|---|---|---|---|
| Stand | Stand | Stand | -0.015467 | -0.007610 |
| Stand | Stand | Draw | -0.015449 | -0.007634 |
| Stand | Draw | Stand | -0.015232 | -0.007845 |
| Stand | Draw | Draw | -0.015214 | -0.007869 |
| Draw | Stand | Stand | -0.011965 | -0.010946 |
| Draw | Stand | Draw | -0.011998 | -0.010918 |
| Draw | Draw | Stand | -0.012318 | -0.010607 |
| Draw | Draw | Draw | -0.012351 | -0.010579 |
The table above advises on proper strategy. First, consider the decision to Stand or Draw on a Player Hand total of five. Note that regardless of the four ways the Banker might play, the expected value on the Player Hand is higher by hitting by a significant margin. The average expected value by standing is -0.015340 and by hitting is -0.012158. If the banker randomized his decisions, the house edge on the Player Hand bet is 0.32% less by hitting than standing.
Assuming the player acting on the Player Hand will draw on a five, how should the player acting on the Banker Hand handle a total of five if the player's third card is a 4? The table above shows the expected value is 0.000028 higher by drawing, regardless of how a Banker Hand 3 vs. 9 is played.
Using the same logic, how should the player acting on the Banker Hand handle a total of three if the player's third card is a 9? The table above shows the expected value is 0.000339 higher by drawing, regardless of how a Banker Hand 5 vs. 4 is played.
In conclusion, in all three situations with free will, the decision-making player should draw.
Banker 3 vs. 9 Analysis
Although I have made my case the expected value of the game is greater on the Banker Hand if the banker hit a 3 vs. a 9, let's look at that situation specifically. The following tables look only at those hands where the Banker Hand has a two-card total of 3, the Player Hand drew a 9, and the player acting on the Player Hand draws on a two-card total of five.
The following table shows the possible outcomes if the banker stands on a 3 vs. 9. The expected value of standing is 0.457205 - 0.390567 = 0.043777.
Stand on Banker 3 vs. 9
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 10,382,475,829,248 | 0.457205 |
| Player | 8,869,227,331,584 | 0.390567 |
| Tie | 3,456,875,888,640 | 0.152228 |
| Total | 22,708,579,049,472 | 1.000000 |
The following table shows the possible outcomes if the banker hits on a 3 vs. 9. The expected value of standing is 0.516019 - 0.371799 = 0.118419.
Hit on Banker 3 vs. 9
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 11,718,056,230,912 | 0.516019 |
| Player | 8,443,028,373,504 | 0.371799 |
| Tie | 2,547,494,445,056 | 0.112182 |
| Total | 22,708,579,049,472 | 1.000000 |
As shown above, the expected value of a banker 3 vs. 9 is 0.118419 by drawing and 0.043777 by standing. The odds strongly favor hitting, by a margin of 7.46%.
Banker 5 vs. 4 Analysis
Although I have made my case the expected value of the game is greater on the Banker Hand if the banker hit a 5 vs. a 4, let's look at that situation specifically. The following tables look only at those hands where the Banker Hand has a two-card total of 5, the Player Hand drew a 4, and the player acting on the Player Hand draws on a two-card total of five.
The following table shows the possible outcomes if the banker stands on a 5 vs. 4. The expected value of standing is 0.95×0.238182 - 0.608714 = -0.382441, assuming a 5% commission on wins.
Stand on Banker 5 vs. 4
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 5,399,045,406,720 | 0.238182 |
| Player | 13,798,139,031,552 | 0.608714 |
| Tie | 3,470,505,148,416 | 0.153104 |
| Total | 22,667,689,586,688 | 1.000000 |
The following table shows the possible outcomes if the banker hits on a 5 vs. 4. The expected value of standing is 0.95×0.262186 - 0.625426 = -0.376349, assuming a 5% commission on wins.
Hit on Banker 5 vs. 4
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 5,943,157,137,408 | 0.262186 |
| Player | 14,176,959,873,024 | 0.625426 |
| Tie | 2,547,572,576,256 | 0.112388 |
| Total | 22,667,689,586,688 | 1.000000 |
As shown above, the expected value of a banker 5 vs. 4 is -0.376349 by drawing and -0.382441 by standing. The odds marginally favor hitting, by a margin of 0.61%.
Player 5 Analysis
The following two tables show the possible outcomes of a two-card Player Hand total of five, assuming the Banker Hand does not have a natural and the banker will hit both a 3 vs. 9 and 5 vs. 4.
The following table shows the possible outcomes if the player acting on the Player Hand stands on a two-card total of five. The expected value doing so is 0.444715 - 0.469428 = -0.024713, assuming a 5% commission on wins.
Stand on Player 5
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 31,757,731,375,104 | 0.469428 |
| Player | 30,085,834,328,064 | 0.444715 |
| Tie | 5,808,447,387,648 | 0.085858 |
| Total | 67,652,013,090,816 | 1.000000 |
The following table shows the possible outcomes if the player acting on the Player Hand draws on a two-card total of five. The expected value doing so is 0.442311 - 0.429768 = 0.012543, assuming a 5% commission on wins.
Draw on Player 5
| Winning Hand | Combinations | Probability |
|---|---|---|
| Banker | 29,074,691,589,120 | 0.429768 |
| Player | 29,923,240,656,384 | 0.442311 |
| Tie | 8,654,080,845,312 | 0.127921 |
| Total | 67,652,013,090,816 | 1.000000 |
As shown above, the expected a Player Hand total of five is -0.024713 by standing and 0.012543 by drawing. The odds favor hitting, by a margin of 3.73%.
Banking Against a Player who Stands on Five
Forgive me if don't go into as much depth analyzing the the Banker Hand strategy if the player acting on the Player Hand were to foolishly stand on a two-card total of five.
With a Banker Hand 3 vs. 9, the expected value is 0.051725 higher by standing.
With a Banker Hand 5 vs. 4, the expected value is 0.005315 higher by standing.
Given the limited free will situations, the Player Hand strategy is what is known as "dominated." In other words, regardless how the Banker Hand plays the two free will situation, the Player Hand should hit on a total of five. Under the assumption the Player Hand will hit on five, the Banker Hand should hit both 3 vs. 9 and 5 vs. 4. Assuming both sides do so, the following are the expected values for both sides of the game. The Banker expected value assumes a 5% commission on wins.
- Player: -0.012351
- Banker: -0.010579
This strategy reduces to the rules of baccarat. If these numbers look familiar, they are the expected values for baccarat. In other words, if two logicians played the limited free will variant of chemin de fer, it would reduce to baccarat strategy.
I should note that if we add free will to a Banker 4 vs. ace, then the player should hit on that. Under the limited free will rules described by Scarne, the Banker is forced to stand in that situation. If the Banker could hit a 4 vs. ace, the rest of the strategy would still be the same as above. The expected values would change, as follows:
- Player: -0.012359
- Banker: -0.010575
Note these expected values are a little better for the Banker and a little worse for the Player. Why they make the Banker stand on 4 vs. ace (as bad play for the Banker), I don't know. Perhaps a mistake in the creation of the rules for baccarat.
Conclusion
Assuming both sides draw in every situation where free will is allowed, as they should, the following are the probabilities of each outcome, assuming eight decks.
- Player win = 0.446247
- Banker win = 0.458597
- Tie = 0.095156
The expected value on the Player Hand is -0.012351. After considering the 5% commission on wins, the Banker Hand has an expected value of -0.010579. These figures are the same as conventional baccarat.
Fleming Rules Analysis
The following is my analysis of chemin de fer, according to the rules in Casino Royale by Ian Fleming. The Doctrine of Chances by Stuart N. Ethier echos these rules as how the game was played in the early 20th century. As explained in the rules section above, Fleming said the game was played with six decks and free will in all situations, barring either side having a natural.
After much analysis, I find there are only six situations where the right play depends on how the other side plays. Here they are:
- Player two-card total of 5
- Banker two-card total of 6, after Player stands
- Banker two-card total of 3, after Player draws a 9
- Banker two-card total of 4, after Player draws an ace
- Banker two-card total of 5, after Player draws a 4
The Banker strategy is to play the same way as the Player. In other words, if the Player hits a five, then the Banker should hit in all four other situations listed. Meanwhile, the Player should play the opposite way the Banker tends to play the four strategy-dependent situations listed.
The following table shows the expected value for both hands according to the two possible strategies for each hand. The Banker strategy refers to how the Banker plays all four of the Banker hands listed above. The Banker expected value assumes a 5% commission on wins.
Full Free Will Expected Values
| Player Strategy |
Banker Strategy |
Player Exp Val |
Banker Exp Val |
|---|---|---|---|
| Stand | Stand | -0.015501 | 0.015501 |
| Stand | Hit | -0.008734 | 0.008734 |
| Hit | Stand | -0.011993 | 0.011993 |
| Hit | Hit | -0.013809 | 0.013809 |
If two logicians played chemin de fer, they would both randomize their strategy, much like in rock-paper-scissors. In particular. In particular, here are the probabilities for both sides:
- Player: Hit on five with probability 78.84%.
- Banker: Hit on the four situations listed with the same 78.84% probability.
As long as at least one side plays the randomization strategy above, the following will be the overall expected values for both sides, again assuming a 0% commission on Banker wins:
- Player: -0.012735
- Banker: 0.012735
I'd like to comment that Ethier draws a different conclusion that I do. This seems to be because he doesn't consider the Banker hitting on six, after the Player stands, to be something he is allowed to do. Instead, Ethier assumes the Banker always stands in this situation.
External Links
- Chemin de Fer Rules by the Gaming Commission of Massachusetts. Note they do not give the banker any free will.
- Wikipedia page on Chemin de Fer.
- The Doctrine of Chances: Probabilistic Aspects of Gambling by Stewart N. Ethier. This college text has several pages devoted to the mathematics of Chemin de Fer.



