Blackjack - House Edge and Rule Sets
In a live casino, if you could find a blackjack table that uses Unified Gaming rules, including a single deck, but deals reasonably deep into the deck before shuffling, would the house edge be different than -0.14%?
Yes, however the edge would actually be less for the basic strategy player in a live casino. This is because in a live casino the dealer will generally deal until a certain point is reached, finish that hand, and then reshuffle. If the deck is rich in small cards (good for the dealer) when the cut card or shuffle point is reached then more cards are likely to be dealt than if the deck were rich in big cards at the shuffle point (good for the player). The effect over thousands of hands is that a disproportionately high number of small cards are dealt which is directly related to a lower player return on investment. The effect is not huge but it is mathematically better to play with the same rules at an online casino as opposed to a physical casino.
For more on this topic, please see my blackjack appendix 10 on the cut-card effect.
When calculating the house edge in blackjack, do you include pushes as you do in baccarat?
Yes. I always include pushes in the house edge. The only exception is certain craps bets that usually result in a push, namely the place, buy, lay, and hard ways, that tend to remain up until resolved. For those bets, I define the house edge as the expected loss per bet resolved.
I see that the odds you've published for single-deck blackjack are in favor of the player. Does this mean that if I play over and over again I have better odds than the house?
It is hard to find a blackjack game where the basic strategy player has an edge over the house. The player edge in single-deck blackjack on my site is based on otherwise multiple deck rules, which rarely exist in single deck. I organized the table this way to illustrate the effect of the number of decks. Unified Gaming offers the best blackjack game for the basic strategy player I have ever seen is offered anywhere. For a list visit my online casino index. If you do play a game with a negative house edge then, yes, that does mean you will have better odds than the house, assuming you play the basic strategy.
Here in Natchez we have a river boat casino that allows the Royal Match (version 1) with blackjack, using six decks. They also have an added bonus that if the player and dealer both get a royal match on the same hand, then the player is paid an additional $1,000. How does this affect the house edge?
This $1000 bonus lowers the house edge from 6.67% to 6.00%, assuming a $1 bet.
Across the various blackjack strategies you provide on your site, does the standard deviation change much? I would guess that when DAS is allowed, one's results are more variable, but how much? Is there a good reference book that provides variance figures for various basic blackjack strategies?
Good question. Unfortunately I don't have exact standard deviation figures according to specific sets of rules. The 1.15 figure on my site is based on liberal Vegas Strip rules. I agree that the double after split rule increases the standard deviation. Surrender would decrease it. Sorry I am not of more help than that.
On your blackjack page, in the House Edge section, you indicate that the player has the edge in single-deck blackjack. Numerous Vegas Casinos offer single-deck blackjack, but I doubt they are dealing a losing game. What gives here? Is your page incorrect or are the casinos just gambling on their clients not being able to play basic blackjack. A friend of mine and I have a bet riding on this. Also. Is it true that with even a simple card counting system a competent blackjack player can consistently walk away a winner in the long run? Thanks for your help.
You have a legitimate point. At the time you wrote this I indicated the house edge according to a fixed set of rules that varied only by the number of decks. However, in real life, when single deck is offered the other rules invariably become more stingy. I have already enhanced the house edge table in the blackjack section to include a wider variation in rules. The typical Las Vegas single-deck game does not allow doubling after a split and the dealer hits a soft 17. With these rules, the house edge is 0.18%. The best single-deck game is at the Slots-a-Fun (next to Circus Circus) where the dealer stands on soft 17 for a player edge of 0.01%. Next door, at the Westward Ho, double after a split is allowed but the dealer hits a soft 17 for a house edge of 0.04%. About card counting, absolutely not, even the best of card counters will lose often. An entire month can be at a loss. Only over the very long haul does a net profit become likely.
Update: Since this writing the Westward Ho was torn down and the Slots-a-Fun has slots only.
Dear Wizard! I'm about to play Blackjack on Finnish site with the following rules:
- 4 decks
- 9-11 double
- one split only
- double after split allowed
- one card to split aces
- dealer stands on soft 17
- European card rule= none
- no surrender
Are these rules a good deal for me? What is the house edge? Thank you for an answer.
The house edge in this game is 0.51%.
Are you confident of your figures on the online software? In particular, do you really have a .53% advantage over the house just with good basic strategy? I’ve never seen anyone give figures of a player advantage before for any rules with only basic strategy.
I’m confident with that figure. It was determined using a random simulation program of mine. I speculate the creators of the software made a mistake and only intended to offer late surrender on tens and aces, as was the case with the preceding version. I called one online casino that uses Unified Gaming and they were not even aware the new software allowed for early surrender on aces. I give the house edge figures as a service to my visitors. (Update Jan 22, 2005: Unified Gaming changed the rules of their game years ago to remove the player advantage)
I have never seen any tips on blackjack where the dealer is dealt only one card. This seems to be a totally different game than regular blackjack. When you take a hit, you are taking what would be the second card of the dealers hand. A lot of online casinos have this game. Do you have any suggestions as to the best way to play these games? Thank you.
It doesn't matter which card the dealer takes. What is important is whether the player can lose more than their original wager if the dealer has a blackjack. For example, at Starnet casinos, if the dealer has a ten up, and the player has an 11 and doubles, then the dealer can draw an ace afterward, for a blackjack, and the player will lose both the original bet and the double. To adjust for this European no-peek rule, the player should be more conservative about doubling and splitting when the dealer has a potential blackjack.
For more information on the European no-hole-card rules, please see my European blackjack basic strategy.
I'm a dealer at Casino Niagara and want to know what the odds of a dealer making a hand are when the up card is a 5. It seems to me and the other dealers that we all agree that we make a hand more times than not, and usually a good one at that. Also, what are the odds of a dealer having a blackjack with an ace as an up card?
You're right, it is more likely the dealer will make a pat hand. From my blackjack appendix 2, the following are the probabilities of the dealer's final total given a 5 as an up card. This assumes the dealer stands on a soft 17, which I believe is what you do.
- 17: 12.23%
- 18: 12.23%
- 19: 11.77%
- 20: 11.31%
- 21: 10.82%
- bust: 41.64%
Assuming 8 decks, there are 16*8=128 10 point cards in the deck. Eliminating the ace there are 52*8-1=415 possible cards under the ace. Thus the odds of a blackjack are 128/415 = 30.84%.
What is your opinion of the continuous shuffle machines now being used at the blackjack tables in Las Vegas? Do these machines give the house more of and edge even when a person is using basic strategy?
For those who don't understand what you're asking, there are new machines that take the blackjack discards and place them randomly back in the deck after each hand. If you are using basic strategy, then the shufflers actually lower the house edge slightly, due to the omission of the cut card effect. It is my understanding that they do provide an honest random shuffle. However, the shuffling machine allows the dealer to waste less time shuffling and spend more time dealing. This means you will spend more time playing, and thus more hands for the house edge to grind you down.
For more information on the mathematical effect of continuous shufflers, please see my blackjack appendix 10.
I think your website is one of the best gambling sites on the net, and I have a question that I am hoping you would be able to answer. There is an Indian casino a few hours from my house that has some odd rules and regulations. I was wondering if you would be able to determine the house edge from these rules:
- There is a 50-cent charge on each hand if your wager is between $5 and $25
- There is a $1 charge on each hand if your wager is $26 to $500.
- You can split up to 4 times, not including aces
-You can double on any first two cards - You can double after a split
- Dealer stands on all 17s
- Early surrender is available
- One card on each hand if you split aces
- $100 bonus on getting 7 cards without busting
- $100 bonus on getting 3 7's in a row
- $500 bonus for getting 3 Blackjacks in a row
- $10,000 bonus for getting 4 Blackjacks in a row
Any help you can give is appreciated.
I'm going to assume that eight decks are used and that the bonuses are not applicable if the dealer has a blackjack. Using the Blackjack Count Analzyer I get a player advantage of 1.4% with a $5 bet. Unfortunately, this advantage is not available at greater bet sizes as the comparable benefit of the bonuses decreases and the additional fee for bets of $25 or over. With a $24 bet the house edge is 1.4%, and with a $25 bet it is 3.3%. This certainly is a very interesting game. If you play it let me know how you do.
What are some of the best online casinos to play blackjack on, with the following criteria in mind - Best player odds, fewest decks, fairness?
Assuming you put the greatest priority on player odds I would have to go with a Unified Gaming casino. You'll enjoy a player edge of 0.57% assuming you following the proper strategy.
First off, great web site! I love it! In Reno I saw a game with the following rules: six decks, dealer hits soft 17, double after a split, re-split anything except aces, and the player could double on any number of cards. For example, the player could draw to a four-card total of 11 and then double. What is the house edge on this game?
You didn't state the surrender rule, so I'll assume it isn't allowed. According to my blackjack house edge calculator, and before considering the double any number of cards rule, the house edge is 0.64%. According to my list of rule variations, being allowed to double on any number of cards (a rule commonly found in Panama) is worth 0.23%. So, the house edge over the overall game is 0.64% - 0.23% = 0.41%.
Here in Finland we have blackjack tables in some nightclubs and restaurants but these tables follow the following rules: six decks, ties push only on 21 and blackjack, ties on 17,18,19 and 20 the house wins!! No surrender, European no hole card rule, double 9-11, unlimited splits! I understand this is a bad deal for players but how bad is it? What is the house edge in this game?
I have actually seen these rules when I went to Helsinki in 1986. Without a doubt, the worst blackjack rules I have ever seen.
To answer your question, my blackjack house edge calculator says the house edge is 0.54%, before considering the rule that ties lose on 17-20. My list of rule variations says the effect of losing on 17-20 ties is 8.38% in the house's favor. So, the overall house edge would be 8.92% (ouch!).
How did you derive the house edge in blackjack?
I wrote my own combinatorial program which cycles through every possible event and keeping a running tally of all the possible outcomes weighted by their probability. Except in cases where re-splitting pairs is involved, my calculations are exactly right.
Can it actually be true that what I experience has a statistical base? It seems to me that it takes a lot longer to win X number of chips that to lose the same amount (I only play blackjack). For example, if I start with 300 chips, it might take hours to double my money (my goal), yet I can lost that number in what seems like almost no time at all. Can this really be true? Also, do you have a rule of thumb about when to leave the table when you are winning?
What you have experienced is likely the result of some very bad losing streaks. It may also be the result of progressive betting or mistakes in strategy. The basic strategy flat bettor should have a roughly symmetrical expectation in terms of steep ups and downs, slightly favoring steep downs due to the house edge and a 48% chance of a losing hand compared to 43% chance of winning. If I'm playing for fun then I leave the table when I'm not having fun any longer.
Can blackjack be beaten under the following casino conditions:
- The game is dealt face up from an 8 deck shoe, with the cut card appearing after 5 decks have been dealt (3 decks behind the cut).
- Dealer stands on soft 17.
- No surrender.
- Can double down on any 2 card total without an ace.
- Can split aces once only, one card on each.
- Can split any other pair to a maximum of 3 hands.
- Can double after split.
- Dealer takes original bets only on blackjack.
- Can take even money on blackjack when dealer’s upcard is an ace.
- Table max is 50 times table min.
- Card counting is permitted if the counter plays the first hand of the shoe, and plays every hand. Counter can play any number of boxes, and any bet amount. Counter can stop at any time, but cannot rejoin a shoe after missing a hand, or join a shoe that is partway through.
I haven't done any simulations, but my educated option is a definite yes, this game can be beaten. The strategy to use in this game would be to bet the minimum when the odds are against you and the maximum when they are in your favor. Normally a sudden 50 times increase in bet size would set off a huge red flag but it seems the counter could do this with impunity in your game. When Atlantic City first opened the casinos could not ask card counters to leave and entire tables were filled with people jumping suddenly from a $5 bet to $300, or whatever the minimums and maximums were. After taking a huge beating, the Atlantic City casinos begged the gaming authorities for a change in the rules, which they got. Not only could this be beaten, but I think it would be a card counters dream.
Michael, thanks for your advice. I have two questions regarding the Odyssey machines that are very popular at Vegas casinos. I like to play their Top Hat blackjack. My first question is how much of a dealer edge do I lose from only getting paid dollar for dollar in winning a blackjack versus receiving the standard 1 1/2 times my bet? Also this machine has a double or nothing feature that seems to give the person a 50/50 chance of winning. Is it worthwhile to use this feature?
If you win only even money on a blackjack, then that increases the house edge by 2.3%. I recommend the double or nothing feature because it is a zero house edge bet. However, only double up on amounts you're comfortable with losing.
I don't have a blackjack simulator personally, but wondered what the house edge would be on the video blackjack here in Rhode Island. It is single deck (reshuffled every round of course), split pairs only once (no splitting unlike tens), double on hard 10&11 only, pull six cards automatic winner regardless of dealers hand (i.e. If you have a soft 19 or 20 after 5 cards, you automatically hit because it is 100% impossible to bust on 6th card) double on splits on hard 10&11 only) split aces receive only one card each. BUT, here's the clincher, split Blackjacks pay 3 to 2 whereas traditionally they pay 1 to one) I know this can make a difference of maybe 0.5 % in the overall house edge. Also late surrender on any hand, and dealer hits soft 17. So, playing optimum basic strategy for these situations, what is the overall house edge. My guess is that it' in the 1.5% range because of the single deck and 3-2 pay out on split blackjacks.
According to my blackjack house edge calculator, the house edge before the 6-card Charlie rule and the 3-2 on blackjack after splitting, is 0.34% with perfect strategy.
My list of rule variations says that the 6-card Charlie rule is worth 0.16%, and a 3-2 paying blackjack after splitting aces is worth 0.19%. It still doesn't pay to split tens. So, the overall house edge is 0.34% - 0.16% - 0.19% = -0.01%. In other words, a player advantage of 0.01%.
I was visiting an Indian casino the other day where the blackjack minimum bet was $2, but for each bet, they asked for an additional 25 cents (they did this by giving you 4 special 25 cent chips for each dollar chip you had) so essentially, you bet $2.25 to win back $2. While I was still able to walk away with a bit of a profit, I was wondering if there was a quick and easy way to calculate just how much of a house edge this "commission" gave them? I know that compared to dealer hitting on soft 17, it's gotta be a killer.
The total house edge is [fee + (house edge)*(bet)]/[fee + bet]. Let's say the house edge is 0.8%. Then the house edge including the fee would be [$0.25 + $2.00*0.008][$0.25 + $2.00] = 11.82%.
However, a quick and easy estimate is to simply divide the fee by the bet as the increase in house edge due to the fee.
Hey Wizard...I have just got into online gambling and have referred to your site for pretty much everything...I appreciate all the information on the single-deck Unified Gaming information, but what about the six deck game? Can you tell me the player (or dealer) edge in this game as well as a basic strategy? It would seem to me that this would be one of the best bets at which to count cards...what do you think? Thank you in advance!
You should follow my multiple-deck strategy but surrender against aces in the same hands as the single-deck strategy. I haven't studied if counting this game is more profitable than the single-deck game, but I would be interested to hear from anyone who is doing as you suggest.
In blackjack, I've read that the dealer breaks about 25% of the time. If that figure is correct, is that 25% of all the hands dealt, or 25% of just the hands that he hits? Also, in blackjack the house edge varies according to the rules of that particular game. What I'd like to know is, what effect, if any, does playing head to head with the dealer have. It would seem to me that both of you will get more blackjacks, thereby reducing the house edge somewhat.
Assuming six decks, and the dealer hits on soft 17, if the dealer is forced to play out every hand them my blackjack appendix 2B says the probability of the dealer busting is 28.58%. However, in a head-to-head game where the dealer doesn't bother to draw cards if the player has a blackjack or busts first, then my blackjack appendix 4 says the probability of busting is 24.36%.
I know that you have the casino advantage for blackjack listed on your web site in the case that a person plays the basic strategy, but I was wondering what the casino advantage was on average against a typical beginner. Also, can you formulate what the best advantage a casino could have over the worst of players, assuming that they would never hit anything higher than a hard sixteen? Thank You Kindly.
According to Extra Stuff by Peter Griffin the cost due to player mistakes of the average player is 1.41%. This is above whatever the house edge is assuming proper basic strategy. It also varies by place, Atlantic City players are better than Las Vegas players, for example. Your other question about bad strategies was such a good one I added information to my blackjack section about it. See my remarks on bad strategies.
Top notch site you are running! My question to you is: by how much does the house edge in blackjack increase if the player cannot afford to split or double?
Thanks for the compliment. That is a good question. Not having enough money to double or split, but otherwise playing correctly, adds 1.9% to whatever the house edge is.
Your web site is awesome! I enjoy your advice and am amazed at the simple way you explain things about gaming in a way I can understand. My question is this -- while playing a benefit blackjack game where they have from what I could tell, all the "Vegas" rules, I found out they were paying two to one for a blackjack. This seems like a big benefit to the player; just how big is it? (this is no joke or prank, I actually played at the table where they were doing this!)
Thanks for the compliment. If I had been at this game I would have played it hard. Assuming six-decks and otherwise Vegas rules, the player edge would have been 1.94%. The 2 to 1 on blackjack adds 2.37% to the player's expected return in a six-deck game.
I just came back from Vegas and played at the Las Vegas Club. They have a game called "Most liberal 21" with the following rules:
- Eight decks
- Dealer hits soft 17
- Double any first two to four cards
- Double after split allowed
- Late surrender allowed
- Re-split aces allowed
- Six-card Charlie
What kind of advantage does the house have with these kind of rules?
At the time you asked this they still paid 3-2 on blackjacks. Before considering the rule about doubling on 3 or 4 cards, and the six-card Charlie, the my blackjack house edge calculator says the house edge is 0.50%. My list of rule variations says that doubling on 3 or 4 cards is worth 0.23%, and the six-card Charlie rule is worth 0.16%. So, the overall house edge is 0.50% - 0.23% - 0.16% = 0.11%.
However, since you wrote they changed their rules to pay 2 to 1 on suited blackjacks and 1 to 1 on all other blackjacks. This increases the house edge by 1.13%, to 1.24%. They still have the sign stating it is the "World's most liberal blackjack," which is patently untrue, if you interpret the word "liberal" to mean lowest house edge.
There is an article in the blackjack section that indicates that a CSM, (Continuous Shuffling Machine), actually lowers the house advantage for the basic strategy player. I assume that is in a heads to head game. Would multiple players increase the house advantage?
That is true. I explain why in my blackjack appendix 10. The number of players doesn't make any difference.
There are a great number of Casinos in the Vancouver area. All except one offer no surprises. However, one of them allows a funky variation on blackjack ... the player may double down or surrender after ANY number of cards until that player stands or busts. Could you please inform me as to how exactly this affects the odds. I would think it would be of great benefit to the player?
According to Basic Blackjack by Stanford Wong, this rule adds 0.2% to the player's expected return. Wong also indicates some strategy deviations under this rule on pages 60-61.
I was sitting at first base in an 8-deck blackjack game. The dealer finished shuffling, and as she put the cards in the shoe she fumbled them slightly, flashing the first two cards: a jack and an ace. Since I knew the jack would be the burn card, I also knew I would get the ace as my first card. This is obviously to my advantage, but how much, percentage-wise? I ended up betting $50 instead of my normal $5 on the first hand from the shoe. I wish it had a happy ending, but I was dealt a soft 18, and ended up busting since the dealer was showing a ten. Thanks for your time, and for the great site!
Thanks for the compliment. I don't have numbers readily available for eight decks, but in a four deck game, where the dealer stands on soft 17, I get the player advantage given that the first card is an ace to be 51.66%. In Basic Blackjack by Stanford Wong he says the advantage in a six-deck game where the dealer stands on soft 17 to be 50.5%. Sometimes a Las Vegas fun book will have a coupon which can be used as an ace for the first card in blackjack. Wong also mentions the kind of situation that happened to you in his book.
I was at the Soaring Eagle Casino in Mt. Pleasant, MI this past weekend and while I was there I noticed a game called "Pitch" blackjack. The game uses 6 decks, which are put into a shuffle machine, and then the machine delivers one "deck" to the dealer. Dealer cuts and deals (usually only two hands for a full table). Then he takes the deck, puts it back in the shuffle machine, and retrieves another 52 card "deck" from the machine. The rules are the same as for a standard shoe game except that the player is allowed to double down with 3 cards if they total 9, 10, or 11. I’m always suspicious of "special" games, so I wondered how the house advantage on this game would differ from a standard shoe game. Does the house have a greater or lesser advantage?
I’ve seen these things at the Las Vegas club, only they cut off two decks out of six I believe. It is a deceptive way to appear to be using fewer decks than are actually involved. Mathematically speaking the house edge would be the same as for the total number of decks in the shuffle machine. Penetration does not matter for the non-card counter. Thus it would not matter whether a machine or a human being cut off two decks from a six-deck shoe, the cards were taken from a six-deck shoe either way.
The Flamingo is offering a single deck blackjack game with regular downtown rules (hs17). The only difference is that they altered the natural payoff to 6 to 5 instead on the normal 3 to 2. My questions are; How does that affect the starting advantage on this game? What would it be? How would it affect the insurance wager? Specifically what would Insurance have to pay in order for the player to get "even money" and be square to the 6 to 5 payoff?
Using my good ol' blackjack house edge calculator normal downtown rules result in a house edge of 0.1896%. In single deck the probability of a player blackjack and no dealer blackjack is 2*(16/52)*(4/51)*(1-2*(15/50)*(3/49))= 0.046492. Reducing the BJ win from 1.5 to 1.2 results in increasing the house edge by 0.046492*(1.5-1.2)= 1.3948%. So the house edge of this game would be 1.3948%+0.1896%=1.5844% (ouch!). For insurance to result in even money, it would have to pay 5-1 but the player could only bet 20% of the original bet on it.
Your house edge calculator is excellent. How do you use it for continuous shuffle games? Also, if the shoe is used, how does the house edge change?
My house edge calculator is based on the first hand after a shuffle. So it is perfectly suited for a continuous shuffling machine game. Contrary to popular belief the house edge is actually slightly higher on a hand shuffled game as opposed to a continuous shuffling machine game. I explain this in more depth in my blackjack appendix 10.
On a CSM blackjack game, 5 deck, what would be the effect of the dealer not putting discards back into the machine every hand if 24 of 52 cards in the discard rack were face cards? What about 48 of 102? What would be the effect if 44 of 52 cards were non-face cards? Can the odds be heavily skewed? I have a feeling that the odds skyrocket in the casino’s favor if the dealer leaves face cards in the discard.
The exact numbers would be difficult to calculate and I won’t get into that. However your speculation is right that the odds favor the dealer if he leaves a lot of high cards in the discard rack yet will put back into play a lot of small cards. This would be the same kind of thing as preferential shuffling, in which the dealer of a hand held game shuffles when the count is good but deals another round on a bad count. Preferential shuffling is something that definitely does happen here in Las Vegas so what you describe would not surprise me either.
Can you please explain the "cut card effect" in Blackjack. Why don’t people use this when quoting BS house edges for various numbers of decks rather than showing BS house edges that take this into account?
I explain all about the cut card effect in my blackjack appendix 10. The reason house edge statistics are based on a non-cut card game is likely out of tradition and mathematical simplicity. However you make a good point that it would be more accurate to inflate the house edge figures to account for the cut card. Yet I am still going to stick to basing my house edge figures on the first hand of a freshly shuffled deck. Blackjack is hard enough to analyze without worrying about the cut card effect all the time.
Hi, which Las Vegas casinos offer the best blackjack game? Is there a website you know which lists the Vegas casinos and their BJ rules? Thanks for any help you can give me.
I usually use Blackjack Conditions and Specials for information on where the best blackjack games are in Las Vegas. Surprisingly they say that Caesars Palace has the best basic strategy game: double deck, double on any two cards, dealer stands on soft 17, and late surrender for a house edge of 0.13%.
You go, wiz. Our local casino hands out promotional coupons, which act as a first-card ace in blackjack. From your BJ appendix, most hands containing an ace have a positive expectation, without counting the BJs you’ll get four out of every thirteen plays. Do you know the overall expectation of having an ace as your first card? Thanks.
According to Stanford Wong’s ’Basic Blackjack’ he says the player’s edge given the first card is an ace is 50.5% (page 124). Your question however could be rephrased as, "what is the value of the ace, given that the other card is not a ten." Using an infinite deck for the sake of simplicity we can breakdown Wong’s number as follows: 0.505 = (4/13)*1.5 + (9/13)*x, where x is what you want to know. Doing some simple algebra we get x=28.5%.
My friend and I are debating two blackjack issues that arose from his Caribbean Vacation. (1) What shift in odds does the dealer NOT drawing the second card have? House favor or player favor? (2) in your simulations, what impact does the number of players have on the accuracy of the odds?
(1) It depends what happens if the dealer does have a blackjack. If the player is guaranteed to lose no more than the original wager then it doesn’t matter if the dealer takes a second card or not. If the player stands to lose the total amount bet after doubling or splitting and the dealer gets a blackjack then that works to the dealer’s advantage. (2) I don’t have to simulate this because the number of players makes no difference.
What advantage does a 6-5 payoff on a blackjack add to the house?
It depends on the number of decks. I have only seen this rule in single decks games, so we’ll assume one deck. The probability of a blackjack in a single deck game is 2*(4/52)*(16/51)=0.0483. The probability of the dealer not having a blackjack, give that the player does have one, is 1-2*(3/50)*(15/49) = 0.963265. So the probability the player has a blackjack and the dealer doesn’t is 0.046492. The casinos keeps an extra 0.3 units every time this happens to the increase in the house edge is 0.3*0.046492 = 0.013948, or about 1.39%. This is a huge increase, making this game the worst blackjack game in Vegas.
Since a $2.50 blackjack pays $4 (extra .25) and since a blackjack occurs every 22 or so hands, I was wondering (at a $1 table) if it would be possible to beat the game (albeit very slowly) by just playing $2.50 each hand?
Actually a blackjack will occur closer to once every 21 hands. To be more specific in a six-deck game the probability of a blackjack is 2*(4/13)*(24/311) = 0.047489. An extra quarter this often is worth 0.25* 0.047489 = 0.011872. Divided by the $2.50 bet this adds 0.004749 to the player’s expected value. Most games where the dealer stands on a soft 17 or uses 1 or 2 decks will have a house edge less than this. So, yes, you could gain a small edge. Assuming six decks and dealer stands on soft 17 the player’s expected profit per hour, based on 100 hands per hour, would be 16 cents.
At the Spielbank Stuttgart, one is given the option in blackjack to take even money immediately if one gets a black jack and the dealer shows a ten or an ace (to avoid a push). Is this a sucker bet? I won 390 euro thanks to your card. Many thanks!
Yes, this is a sucker bet, especially with a 10 showing. This is equivalent to taking insurance. The casinos here always offer "even money" in this situation and both dealer and other players will treat you like a fool if you decline it. However the expected value of a blackjack when the dealer has an ace showing is 1.04 units, better than the 1.00 units you’ll get by taking the even money. So unless you’re a card counter and know the remaining deck to be 10-rich then always decline even money. I’m glad my basic strategy helped you win.
The Mohegan Sun casino here in Connecticut recently added a limited number of blackjack tables that don’t seem to be addressed in your synopsis. It is a 4 deck shoe dealt from a Shufflemaster that, essentially created an infinite deck, inasmuch as the dealer puts the dead cards back into the machine for reshuffling pretty much as the completion of each round of decisions. The game allows splitting to 4 times, double down on splits, dealer stands on all 17’s, early surrender, and double on any first 2 cards except 10’s and face. I have had some very good luck at this game and was wondering if it is one I should continue to play or switch back to the conventional 6 or 8 deck shoe.
There is a common misconception that a continuous shuffler is equivalent mathematically to an infinite deck game. It is not. If the first card dealt is an ace, for example, the probability that second card is an ace is slightly less than 1/13, because one ace has already been removed from the shoe. As I have explained in great detail in my blackjack appendix 10 a continuous shuffler actually lowers the house edge marginally compared to a cut card game. However the dealer never stops to shuffle so you are being exposed to more hands per hour, so expect to lose more per hour. I doubt very much they allow early surrender at the Mohegan Sun, if they did the player would have an edge of 0.28%. Assuming you really meant late surrender the house edge is coincidentally 0.28%, according to Blackjack Edge software.
Some casinos are now offering a single-deck BJ game paying only 6:5 odds for a natural. What does this do to the house edge?
This increases the house edge by 1.39%! This is by far the worst blackjack game in Vegas.
What would be the house advantage for single deck, hit soft 17, double after split, split to total of four hands, double any first two cards, one card on split A’s, Blackjack pays 6 to 5?
This is a popular new gimmick here in Vegas. Many casinos here have prominent signs saying "Single Deck" blackjack. However on a much smaller sign it says "Blackjack pays 6 to 5." Aside from the 6-5 rule the house edge would be 0.05%. However the 6-5 on blackjacks costs the player an additional 1.39%, for a total house edge of 1.44%. This is by far the worst blackjack game in city and I urge you to avoid it.
What advantage if any does the house have when using a six spot layout verses a 7 spot layout?
They can deal more hands per hour in a 7-spot game. However the advantage per hand is the same. Personally I hate these 7-spot tables.
Dear Wizard, I was recently playing blackjack with somewhat of a card-shark who also happens to be my friend. We played casino rules, with one deck- and switched the deal after each time the deck expired. Later, while I was shuffling- I noticed two 9 of spades side by side. My friend obviously claimed he did not know about this, but it seems unlikely. My question is, if you were playing in a similar scenario and were to add one card to the deck, which card would be most advantageous if only you knew about it. Thank you for your time.
From my blackjack appendix 7 we see that each 9 removed from a single deck game increases the house edge by 0.20%. However if you were going to cheat it would be much better to remove an ace, which increases the house edge by 0.58%. If you were to add a card as the dealer you should add a 5, which increases the house edge by 0.80%. So, the best card for the player is the ace and the best for the dealer is the 5.
Can You tell me the expected return in Black Jack if a player wagers all his money in one hand and not having money for split’s or double’s. Thank You.
If you can’t double or split that adds 1.9% to whatever the house edge is otherwise. This just goes to show that you should always have double or split money available if you need it.
Dear Wizard, Just a quick question, why does the house edge change for an insurance bet in blackjack depending on the number of decks used?
Because we already know an ace has been removed for the shoe. That leaves the rest of the shoe slightly ten heavy. A greater the ratio of tens in the shoe the more likely the insurance bet is to win. The fewer the decks the greater this effect is. Insuring a 20 (except A/9) increases the house edge on the insurance bet because there are two less tens in the shoe.
Mr. Wizard, I just recently played on a Casino Boat that had a Bust Bet at the Blackjack table. You could place this even money bet at anytime after seeing the dealers’ up card. Is this a bad bet and what might the odds be? Thank You.
This is a sucker bet. The most likely time the dealer will bust is with a 6 up. However even then the dealer will only bust 42% of the time, give or take depending on the exact rules, for a house edge of 16%.
Some friends and I were in AC last weekend at the Claridge, where we spent the evening playing something called "Multiple Action Blackjack." If you do not know about it, basically, you can bet either 2 or 3 times. You are dealt your hand and the dealer is dealt one card (face up). You hit/stand/double/split as in normal AC blackjack. The dealer resolves the first bet normally, then keeps the original face-up card and starts all over again, resolving the 2nd bet, and then the 3rd. Essentially, you are playing the same hand 2-3x vs the same dealer "face-up card".
It seemed to us that this changed the strategies for blackjack somewhat. It seemed to place a higher priority on staying in the game (not hitting on various soft hands) so as not to lose 3 bets at once by going over. For example, with the dealer showing an 8, you would normally hit a 16, but in this game, it seemed as if we were better off standing on 16 and hoping that the dealer busted at least once out of the 3, thus losing 2 out of 3 rather than 3 out of 3 for busting ourselves.
I was wondering if you’d heard of this variation and how it changes the basic strategy for blackjack. I’m also wondering what the House Edge is for this version as opposed to normal blackjack played in AC.
The strategy for Multiple Action Blackjack is the same as regular blackjack. By standing on 16 against an 8 your chances of a total loss are less. However the safe thing to do is not always the right thing to do. Hitting will result in a greater chance of winning 2 or all 3 hands. Think of it as playing the same hand three times in a row. What is right for one hand is right for three hands, or any number.
I play at a local casino that offers a 6 deck, h17, DAS, DOA game. However, they pay 2-1 on a suited blackjack. How much does that reduce the house edge? How would you figure this out mathematically?
The probability of a suited blackjack in a 6-deck game is number of suits * number of aces of given suit * number of tens of given suit / number of 2-card combinations out of 312 = 4*6*24/combin(312,2) = 576/48516 = 1.19%. I assume a blackjack tie is a push, so the probability of a suited blackjack, when the dealer does not have a blackjack is 1.13%. Getting an extra half unit 1.13% of the time cuts the house edge by 0.57%. In this case the house edge goes from 0.62% to 0.05%!
Wizard- In a recent Ask the Wizard column there was a mention of Multiple Action BlackJack which I had played very successfully several years back at Foxwoods. I had a feeling there was a larger advantage to the player when the deck had excess A’s and 10’s since if the player hit blackjack he had it for all three hands while the dealer had to make a blackjack each time with his/her three hands. If this is true please do not post this on the site since it will be the end of this variation - it is no longer offered at Foxwoods. I find your site very informative and appreciate all your hard work.
Thank you for the kind words. Much like multi-play video poker the house edge is the same for multiple action blackjack as regular blackjack, assuming the same rules. It is true that if the player has blackjack he wins on all three hands. However if the player has a 16 he has to play it on all three hands. Overall everything balances out.
If the house edge in a shoe game of blackjack is "x" percent for the first hand after a shuffle, does the house edge also work out to be exactly "x" percent on average if you play through the entire shoe (assuming flat betting and basic strategy)?
In a cut card game the answer is no. However in a game where the dealer dealt exactly x hands every shoe the answer would be yes. The reason is hard to explain. For more information please see my blackjack appendix 10.
Here in Ontario, people have the opportunity to "piggyback" a blackjack player instead of waiting for a spot at a full table. When the primary player doubles or splits, the piggybacker has the option but not the obligation to do so. If the primary player splits and the piggybacker doesn’t, the piggybacker’s original bet moves to the primary player’s first new (post-split) hand. This seems like it would be beneficial in some cases, for example 8,8 vs 10. In this case, E(16 vs 10) < E(8 vs 10) < 0, so the primary player should split but the piggybacker shouldn’t. In this case, the piggybacker has turned his 16 into an 8 for free. Assuming the primary player plays perfect basic strategy, what is the house edge for the piggybacker? If the primary player colludes with the piggybacker to maximize total winnings, and primary bets $5 while piggybacker bets $100, is it possible to overcome the house edge?
I have seen this rule at the casino in Montreal as well. Yes, this is a good opportunity for player collusion, where the seated player bets small and makes sacrificial plays for the big bettor in back. Basic Blackjack by Stanford Wong goes into great depth on this topic. There are lots of changes to the splitting strategy, for example the seated player should always split twos and then the back bettor should play both hands against a 4 to 6, otherwise play only one. Using Wong’s full strategy reduces the house edge by 0.2%.
Hello Wizard, When I use your calculator for BJ it shows a huge differential in house advantage between a single deck and Double deck. Would there be a difference in the double deck house advantage if the deck is cut in half? What would be the difference in the house advantage for any number of decks if you cut off a larger portion of the deck?
The house edge for a double-deck game is the same regardless of how many decks they cut off. Many dealers incorrectly claim that a double deck game cut in half has the same odds as a single deck game. It does not. Unless you are counting the placement of the cut card makes no difference.
Is it permissible table etiquette to double down with your money (and the risks and rewards are yours) for a fellow player who refuses to double because of lack of money, fear or ignorance? [Actually I did do that for/with a woman who could not double an obvious double hand (I believe 10 against dealer 4) because she did not have enough chips. The dealer was encouraging her to "double for less" although the dealer permitted me to make this player the short term "loan". And I won, ha-ha! If so, could you conceivable turn the house’s edge in your favor?
As long as both players are agreeable then the casino is unlikely to stop you. In some situations it may not be practial because the player may want to take more than 3 cards. However with 10 against 4 the player should never take a fourth card, thus it was a good idea. Although a bit impractical you could always offer to buy the player’s hand and then you play it yourself, if you can agree on a price. My blackjack appendix 9 shows the fair value of all hands. As an example suppose another player had blackjack and the dealer had an ace up. Most players would take even money. You could make money by offering that player more than even money, but less than 103.8%, and then playing out the hand yourself. However don’t extend this offer to a card counter.
You have the greatest gambling site in the world!! If I follow the basic strategy chart intended for "shoe" games in a double deck game what percentage am I sacrificing? Or if I use the double deck strategy in a shoe game what am I losing?
Thank you for the compliment. Assuming the dealer hits a soft 17 you are adding 0.012% to the house edge by playing 4-8 deck strategy in a two deck game. Playing double deck strategy in a 6 deck game costs 0.008%. To take this question further I wondered about a more extreme case of playing 4-8 deck strategy for the dealer standing on soft 17 in a single deck game where the dealer hits a soft 17. In this situation the incorrect basic strategy adds 0.038% to the house edge.
While in northern Michigan I came across a new blackjack rule on splitting aces. Instead of resplitting you still only receive one card but you may double on it if you like. Can you tell me the effect of this rule?
I’ve never heard of this rule before. According to my analysis, being allowed to double after splitting aces decreases the house edge by 0.08%. However not allowing resplitting any pair, compared to resplitting to four hands, increases the house edge by 0.06%. So the combination of the two rules decreases the house edge by 0.02%. Following is the basic strategy of when to double after splitting aces, assuming 4 to 8 decks and the dealer stands on soft 17:
Soft 12 to soft 16: double against anything
Soft 17: double against 2 to 9
Soft 18: double against 3 to 6
Soft 19 to 21: never double
Hello Wizard, great site with a wealth of information! My question is this: How much does the house advantage increase when they change the rule from double after split allowed on anything, into Double after split allowed except on aces? I wanted to make sure this wasn’t a huge house advantage increase like the 6-5 blackjack payout change.
Thanks for the kind words. I think I answered this before somewhere but being allowed to double on split aces gives the player an extra 0.08% in expected value. Nowhere near the 1.39% that the player loses by the 6 to 5 on a blackjack.
First, two columns ago, (May 30, 2004) someone asked about splitting aces and then doubling. You seemed to answer it as if the question meant you could double after you received the second card on top of the ace. I read the question as meaning you could double on the ace only, as if it were two cards that added up to 11. I think that would impact your response, but I'm not sure by how much.
Yes, I interpreted the question that the place could after the second card was dealt to the split aces. If the player could double on each ace alone then that would reduce the house edge by 0.21% (based on infinite decks). With an ace alone the player should opt to double against any dealer up card.
I live next to a local casino that doesn’t use 50-cent chips for the Surrender Option so I get back more than half when I place an odd-numbered bet. In particular the surrender value of a $3 bet is $2. What is the effect of this rule and what are the strategy changes, if any?
This is a great rule! Only losing one-third of your $3 bet by surrendering adds 2.25% to your expected return. You didn’t tell me the other rules but if we assume a house edge of 0.5% before the surrender rule then the player edge afterward would be 1.75%. Here are the hands you should surrender on based on a six deck game (hit or stand on soft 17 doesn’t matter).
- Player 6 against 10.
- Player 12 or 13 against dealer 9, 10, ace.
- Player 14 or 17 against dealer 8, 9, 10, or ace.
- Player 15 or 16 against dealer 7, 8, 9, 10, or ace.
The only hand you would normally split that favors surrendering is 8,8 against a 10. This advice only holds true for a $3 bet. The value of surrendering diminishes as the odd-numbered bet gets higher.
I received a promotion from a casino that offers to return half my wager if the dealer gets a blackjack. How would it affect the house edge and would there be any strategy change to play it optimally?
That is a great offer. Assuming six decks the dealer will have a winning blackjack with probability 2*(4/13)*(24/311)*(1-2*(95/310)*(23/309)) = 4.53%. So a half bet every time that happens is worth 2.27%. Assuming a house edge of 0.5% the player advantage would be 1.77%. The strategy is the same as regular blackjack. Too bad I missed that one.
At the Privilege Casino you can’t split aces, but you can double. How would it change the strategy assuming Cryptologic rules 6 decks and how does it increase the house edge?
Not being allowed to split aces increases the house edge by 0.18%. You should only double against a six, otherwise hit.
Is the Super Sevens side bet countable?
Yes! If you count sevens as -12 and all other cards as +1 then the odds on the side bet swing to the player’s advantage with a true count (running count divided by remaining decks) of 5 or greater. According to my simulations in six-deck game with no three-card guarantee and 75% penetration the true count is 5 or greater 23.2% of the time and the player advantage at these times averages 27.3%. In the game with a three-card guarantee the average advantage goes up to 29.1%.
I have a Blackjack question that I did not see already answered on your site. How would the house edge change if the player always got a glimpse of the dealer’s hole card and changed his strategy accordingly?
According to my calculations this would give the player about an 8.8% advantage under optimal strategy. The optimal strategy is the same as that of double exposure in most cases. However if you think the dealer will expose his hole card again I would recommend not making it obvious that you know and not make plays that normally look ridiculous (like hitting a 19 against a 20) .
What is the added house edge in blackjack if players are never allowed to double nor split?
No splitting costs the player 0.58%.
No doubling costs the player 1.47%.
No splitting nor doubling costs the player 1.91%.
I’ve seen video blackjack in several LV casinos and am wondering if the game is regulated in a similar fashion as video poker. If so, would playing the games using basic table blackjack strategy give the player the best payback percentage? If not, is there a basic strategy for video blackjack?
Yes. Any video representation of a card game in the state of Nevada must be dealt from a fairly shuffled deck. In other words you should expect the same kind of outcome as in a live game with the same rules. So basic strategy tables will also work for video blackjack.
[Bluejay adds: Every video blackjack game I’ve seen pays only even money on naturals, which significantly increases the house edge.]
Sometimes the dealer exposes his hole card in blackjack. What is the correct basic strategy when that happens?
Stanford Wong gives such a basic strategy in his book Basic Blackjack, see table 46. He also said that in 1995 the Bourbon Street casino in Vegas had a promotion in which every 50 minutes the dealer would expose both his cards for five hands. The player advantage during those was about 10%, according to Wong.
I have been researching Casino Bar because they have a nice bonus today. I ran across your claim that their software does the equivalent of "dealing seconds", but I see that your information was last updated about two years ago. I was wondering if you know of any change in that situation, please. I suspect you would have updated the page if there had been a change, but I thought I would ask. Where could I find a basic strategy sheet for a casino dealing seconds? (the bonus may or may not still be playable). Am I right in thinking the house edge is close to 5% in such a game? Of course, if that is the case I may as well play tricard poker. Thank you for a great website. Do you accept donations?
When I find a casino is not playing fair I don't generally go back to check if they've stopped. Sometimes I do if requested by the casino and I feel the problem may have been accidental. Following is a basic strategy, based on infinite decks, where the dealer stands on soft 17 and deals seconds. What I mean by dealing seconds is that if the third card, and only the third card, would break the dealer it is skipped and the next card is played, whatever it is. Otherwise play continues normally. The house edge under this game would be 9.3%. I used to ask for donations but got so few I quit asking. Now the site is comfortably supported by advertising revenue anyway.
What is the advantage to a player to add one ace to and remove one 2 from a 6-deck BJ game with AC rules?
My blackjack appendix 7 can be used to approximate the answer to this question. Adding the ace would favor the player by 0.005816/24 = 0.00024. Removing a two would favor the player by 0.003875/24 = 0.000161. So the total effect would be 0.000404, or a decrease in the house edge of 0.04%.
My local casino has a rule where if the initial 2 cards, for example a pair of 4s, are split to form 2 hands and then the next card is another 4, if the player opts not to split again he will not be given the option to split should a 4 come out as the next card on the second hand of his initial split. My question is: does this rule give the house an advantage and if so, how?
No. If splitting is the right play you should do it every time, and if not never. So this rule is moot if you play properly.
Love the site!!! Amazing! Now, according to your BJ House Edge Calculator with 6-deck, dealer stands on soft 17, double on any first two cards, late surrender, and resplit to four hands the house edge is 0.334%. Can you tell me why a similar calculator at a reputable source (QFit) gives a house edge under the same rules of 0.325%, or 0.009% lower?
Thanks for the compliments. There are several assumptions going into the calculation that may cause the small difference. For example are the cards shuffled after every hand or is a cut card used? Does the player use total dependent basic strategy or composition dependent basic strategy? Is rule interaction factored in, or is the calculator simply adding up the effect of each rule? My figures are based on a random simulation using total dependent basic strategy, both of which work against the player, which may be the reason I come in a little higher. It also may be due to an insufficient sample size in the random simulation. Despite all these factors I think the difference is still negligible: just one bet per 11,000 hands played.
I play video blackjack using basic strategy at Harrah’s Cherokee Casino in NC. They only have $2 machines that previously had paid the usual $3 on a blackjack (3:2) and $2 on a win. Now they have replaced these machines with ones that pay $13 on a blackjack but only $1 on a win. Have you ever heard of machines with these pay schedules? If so do you know how they compare to the normal 3:2 machines? If it helps the dealer stands on a soft 17 and doubling is not allowed after a split. Thanks - have a happy new year and thanks for providing much very helpful information!
You’re welcome. This is an interesting game. Assuming all wins except blackjack pay 1 to 2, and blackjacks pay 13 to 2 I get a player advantage of 0.7%, assuming six decks. Here is a basic strategy for that game.
I’d like to know the house edge on blackjack after having 10% rebate on loss. When it’s 8-deck and 6-deck, are the house edges different?
It depends on your playing behavior. Your advantage can get very close to 10% if you play aggressively, always betting half your bankroll, until you multiply it many times over or go bust trying. My advice is keep your sitting short and go for a big win or lose it all, whichever comes first.
Great site! I would call it the best among all the gambling sites I have seen on the web. A question about surrender in blackjack. Some casinos (for example Foxwoods) give match play coupons for blackjack. One good thing about the coupon is that when you surrender, you only lose half of your own money, and are allowed to keep the whole coupon. (But you lose your coupon no matter you win or lose.) I guess you want to surrender more in this situation, but was wondering what is the correct strategy? Thanks!
Thanks. You should be doing a lot of surrendering if you can keep the match play. My blackjack appendix 9 is good for questions such as this. A match play is worth just about half of face value. So if the expected value of the hand is less than -1/3 you should surrender. Assuming the dealer hits a soft 17 here are those times.
- Player 6 vs. 10-A
- Player 12 vs. 9-A
- Player 13 vs. 8-A
- Player 14 vs. 8-A
- Player 15 vs. 7-A
- Player 16 vs. 7-A
- Player 17 vs. 8-A
- Player 8,8 vs. 9-A
The strategy is the same if the dealer stands on a soft 17, except the player will not surrender 6 against an ace.
I deal a blackjack game for friends every now and then using only 2 decks. I was wondering what the best house edge is in regards to how many hands to deal to and splitting and doubling down rules. Thanks in advance. Hope you have the time to answer my question. If not I understand.
In my opinion the dealer should set the rules on the liberal side in home games. Screwing your friends with stingy rules is just not cool. If you use double decks I would recommend double on any first two cards, double after a split, and dealer stands on soft 17. Otherwise standard rules. That will result in a house edge of 0.19%. However player mistakes should give you much more than that.
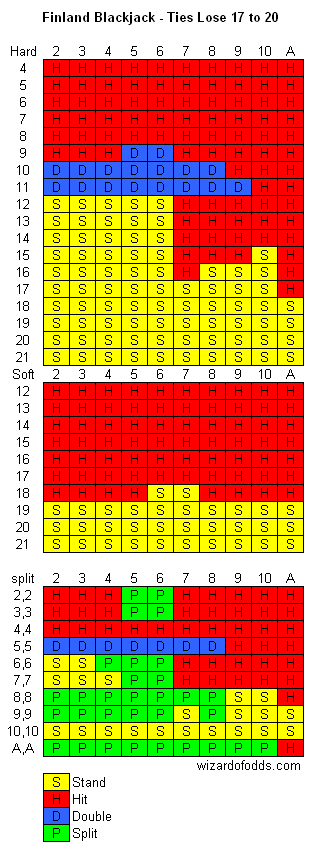
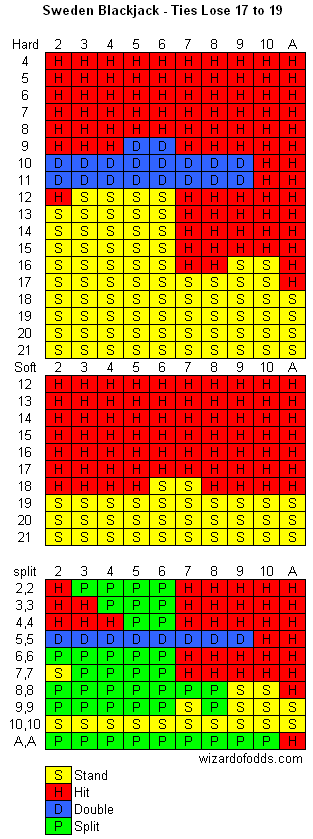
Sir! What is or where we can find the best basic strategy for Club Blackjack as played in Finland, Sweden and Baltic Ferries. 6d, NHC, DD9-11,1Spl, NDAS,dealer wins ties 17-20 (17-19 in Swd). We understand that this is a complete suckers game with house edge of nearly 9% but it is the only game in town and since we cannot win we would at least die fighting as good soldiers are expected to do. Thank You!
I’ve actually seen those rules when I went to Helsinki in 1986. I was only 20 at the time and I’m embarrassed to say I actually played the game, because I still underage in the U.S., and was still years away from becoming the Wizard. In fact it would have been the first legal game of blackjack I ever played. Meanwhile there was a single-zero roulette table right next to it.
I assume the dealer stands on soft 17 in both cases. It is my understanding that double after a split is allowed in Sweden but not Finland. Assuming that I get a house edge of 5.99% in Sweden and 8.93% in Finland. Here are the basic strategy charts.
 |  |
In a recent Ask the Wizard column, a reader wrote asking about a $2 video BJ game in North Carolina that pays $13 for a BJ and $1 for any other win. What the reader did not understand is that the payouts are NOT 13:2 for BJ and 1:2 for other wins... instead the payouts are 13 for 2 on BJ and 1 for 2 on all other wins. Like a slot or video poker machine, this machine takes your bet as soon as you hit the "Deal" button. Then, if you "win", it pays $13 for BJ or $1 for OW. In other words, the player actually loses money on any non-BJ win. Given these payouts, what is the EV for a single deck game?
And I thought the rules in Finland were bad. I’m assuming that ties lose. It wouldn’t make any sense for ties to push, which would be better than a win. So if ties lose, wins lose half, and blackjacks pay 11 to 2 the house edge would be 51%!
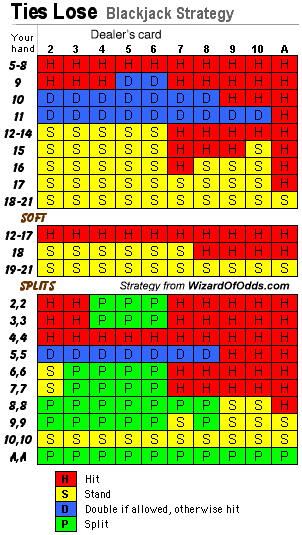
I deal blackjack at my church festival and I’d love to run a basic strategy scenario for our rules...
4 decks
Dealer stands on soft 17
Double on 9,10,11
Split any cards
Double after split
PLAYER LOSES PUSHES
The last rule is what I call’s "God’s House Advantage" and is the one rule that obviously is not in any of the strategy generators I’ve found online. I’m convinced that the push loses rule might make hitting a 17 a basic strategy play in some cases. Best regards and keep up the great work.
Isn’t there a commandment in the bible about stealing? I show the house edge of that game is 9.3% (ouch!). Here is the appropriate basic strategy for this variation of Ties Lose Blackjack. See column #110 for the version where the player can double on soft hands.
Fantastic site — A gambling bible no less. Which would be the better rule for the player in an otherwise normal blackjack game with six decks. The first rule is the insertion of two jokers in the shoe. If the player gets a joker in his first two cards it is an automatic winner, paying even money. If a joker comes out at any other time, including to the dealer, it is burned. The second rule is a Five-Card Charlie.
Thanks. The probability of getting at least one joker in two cards dealt from a 314-card shoe is 1-(combin(312,2)/combin(314,2)) = 1.27%. So the probability is 1.27% of turning an average hand into an automatic winner. If we assume an average hand has an expected value of −0.005 then the value of the first rule is 0.0127*(1-(-0.005)) = 1.28%. You can see from my blackjack section that the five-card Charlie rule is worth 1.46%. Assuming the cards are shuffled after every hand, or you are forced to flat bet, then given the choice as a player I would pick the five-card Charlie rule. However, the joker rule would be very easy to exploit further. The greater the ratio of jokers to cards in the shoe the more you should bet. With at least 50% deck penetration, this should easily be enough to make it the better rule.
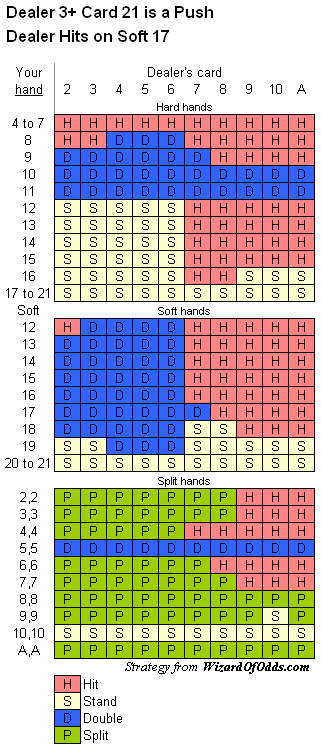
In Reno there is a new type of positive EV promotion. The dealer pushes all “dealer draw to 21s”. Dealer naturals still win. (Any strategy suggestions? Table limits are $5-$25, I always play the max. The basic game is 6-Deck H17 DAS RSA to 4 hands.
Wow! According to my calculations this results in a player advantage of 6.4%. I’m assuming that the rule applies after doubling and splitting. Here is the basic strategy for that rule.
What effect does the ’rule of 45’ have on the house edge, if any. I understand the rule of 45 to be that you stand on 16 vs. 10 if your cards include either a four or a five. Obviously this would be pointless if counting, as the count would be a better indicator of when to stand on 16.
It is correct that in general if your 16 has at least one 4 or 5 in it then the odds genrerally favor standing. This is obviously because a 4 or 5 will give you a 20 or 21, and there is at least one less of them in the remaining deck. 16 against a 10 is so borderline that this effect can make the difference in the play. In a two-deck game, I show following the rule of 45 lowers the house edge by 0.015%. In a six-deck game it only lower the house edge by 0.003%.
At a recent charity casino night (not real money) there were some unusual rules for both Blackjack and Craps, and I wasn’t sure which to play. In BJ, Dealer stand on Soft 17, Double after splitting alowed (except on aces), Doubling allowed on 3 cards, BJ pays 2:1, no insurance, no surrender. In craps, COME bets paid 2:1 on 4 and 10, but no odds allowed on COME bets. I played craps until the table just got so crowded it wasn’t any fun any more, but I suspect my pass line / always COME strategy was better odds than I got at the BJ table. Was I right?
As my blackjack section shows, the 2 to 1 on blackjacks is worth 2.27% and doubling on 3 cards is worth 0.23%. Otherwise the rules look standard. All things considered, the house edge in the blackjack game has a player advantage of 2.1%. The probability of winning on a 4 or 10 in craps is (6/36)×(3/9) = 5.56%. Every time this happens you get an extra unit, so it is worth 5.56%. Normally the house edge on the come bet is 1.41%, so overall the player edge under this rule is 4.15%. So I agree that craps was the better game to play.
The Firelake Casino in Shawnee, Oklahoma charges a 50-cent commission on each $5 blackjack bet. The other rules are the standard, standing on all 17s. A promotion pays an extra $25 for each suited blackjack, $100 for suited 7-7-7 or 6-7-8, $125 for ace and jack of spades.
Assuming six decks, the probability of a suited blackjack is 4×6×24/combin(312,2) = 1.19%. So the $25 bonus on that is worth $25×0.0119 = $0.2968 per hand. The probability of a suited 7-7-7 is 4 × combin(6,3)/combin(312,3) = 0.000015957. So the value of $100 on that is $0.0016. The probability of suited 6-7-8 is 4×63/combin(312,3) = 0.00017234. So $100 on that is worth $0.0172. The probability of a suited ace and jack of spades is 6×6/combin(312,2) = 0.0007420. So $100 extra on that is worth $0.0928 (the player is already getting $25 for the suited blackjack). Adding this all up, the bonuses are worth 11.25 cents. So this is nowhere near enough to compensate for the 50-cent commission.
I play at a casino in London that offers single deck blackjack. The player can play three hands: thus, there are a lot of cards exposed. Do you know of any tables/calculator that works out the exact composition best play in these circumstances.
The blackjack calculator at gamblingtools.net (www.gamblingtools.net/bj/ppbj.html) is perfect for this kind of game. Now you just have to get the casino to let you use your computer at the table.
Could You please make a chart for Party Poker single deck blackjack. Also, with best play, what are the odds.
As I read them, the rules are:
- 1 deck
- Dealer hits soft 17
- Double only on 9 to 11
- Double after split allowed (subject to 9 to 11 rule)
- No surrender
- Blackjack pays 3 to 2
- Dealer always peeks for blackjack
Here is the basic strategy.
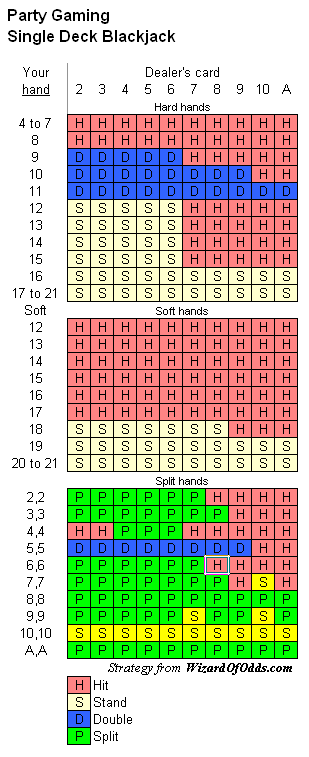
The house edge under these rules is 0.16%.
A local casino is offering a action chip bonus to their O/U 13 sidebet. If you bet at least $5 on your hand and a minimum of $5 on either the O/U bet, if your first two cards are suited, you win a $5 action chip. If you suited hand matches the dealers, you win $10 in action chips. The action chips can only be used for a regular BJ bet, if you win a bet using the action chip it is replaced with a casino $5 chip, if you push you can use again for another hand, it cannot be used for DD’s or splits. Is this game worth playing, $5 a hand with $5 O/U bet?
Assuming six decks, the probability your cards will be suited, but not suited to the dealer’s up card is (77/311)*(234/310) = 18.69%. The probability your two cards and the dealer’s up card will be suited is (77/311)*(76/310) = 6.07%. From my blackjack appendix 4, we see the probability of a win in blackjack is 42.39% and a loss is 49.10%. The probability of a win before a loss is 42.39%/(42.39%+49.10%) = 46.33%. So an action chip is worth about 46.33% of face value. The value of this promotion is 46.33%*(18.69%*$5+6.07%*$10) = 0.7142, or about 71 cents per hand. The expected loss on a $5 blackjack bet is about 3 cents. From my blackjack appendix 8, we see the house edge on the over-13 bet is 6.55%, so the expected loss on a $5 bet would be $5*0.0655 = 0.3275. Therefore, the expected loss due to the house edge of both bets is about 36 cents, and the expected gain is 71 cents, for a net gain of 35 cents per pair of bets.
What is the house edge in video blackjack?
It depends on the particular rules, but it is usually high because of a common rule that blackjack pays only even money. I checked at the Suncoast and they have the following rules: one deck, dealer stands on soft 17, blackjack pays even money, late surrender allowed, player may only double on 10 or 11, double after split not allowed, split aces get one card each, only one split allowed, six card Charlie, dealer must stop with six cards. The house edge of this game is 2.39%.
Hi Wizard, always love your columns and miss those personals. I have a question about a blackjack variation. The following is the "on fire" blackjack rule from an online casino I have recently played at.
In order to be "On Fire" you must win three hands in a row. You will notice the On Fire gauge at the bottom of the game screen. When this gauge fills up, you will be on fire. Once you have accomplished this, all winning blackjack hands pay you at 2-1 odds instead of 3-2 odds, dramatically increasing your potential pay out. However, if you are on fire and you lose a hand, you lose your current on fire status and must go back and try to win three hands in a row. Pushed hands do not affect your On Fire status.
How much does this lower the house edge? Would it be +EV if you raised your stakes every time you were On Fire? Would love to hear your thoughts. The casino is jonwoodgaming.com, by the way. Thanks
My blackjack appendix 4 shows the probability of a net win, loss, and draw in blackjack are 40.59%, 42.69%, and 12.44% respectively, assuming Atlantic City rules. The probability of a win, not counting ties is 40.59%/(40.59%+46.97%) = 46.36%. The probability of three consecutive wins, skipping ties, is 0.46363 = 9.96%. Assuming six decks, blackjack paying 2 to 1 is worth an extra 0.02267. So this gives the player 0.0996*0.02267 = 0.002258. The house edge is usually higher than that, but it is a nice reduction. All this assumes you are flat betting. If you could bet more on the "on fire" hands you could destroy them with a house edge of 1.5% to 2.0%, depending on the specific rules.
Hi Wizard. Thanks for maintaining this web site! I have a question about a blackjack rule that is applied in Dutch casinos: When being dealt a pair of sevens, a third seven will earn you 2:1 on your bet, regardless if you win the hand or not. However, this only applies when the sevens have NOT been split. I know that there are 6 dealer up cards in basic strategy that allow splitting sevens and 7 that do not, so the player should have an edge in this particular situation. But what are the odds of being dealt 3 sevens in blackjack in the first place? And if dealt 3 sevens, what are the odds they qualify for the 2:1 pay-out rule, based on a 4 to 6 decks, dealer stands on soft 17 basic strategy chart? Hope you can figure this one out for me. Keep up the good work!
I show that rule is worth 0.026% to the player. Despite the incentive to hit 7,7 against a dealer 2-7, the player should still follow basic strategy and split.
Sir! There is a private game variation of blackjack played with a Spanish-style 40-card deck with no 8s, 9s & pip tens. Where can one get or what would be the basic strategies for those games? This game is played in Finland, usually played with a bottle of spirits and one’s personal knife close at hand. Thank you for your time!
First the dealer wins ties and now this. Finland has got to be the world leader for unusual and lousy blackjack rules. Here is your basic strategy.
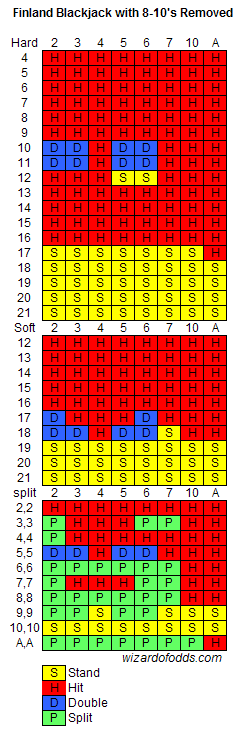
Assuming six decks, no dealer hole card, dealer stands on soft 17, no surrender, double after split allowed, and resplitting aces allowed, I get a house edge of 1.86%.
I read somewhere that half a counter’s edge is in taking insurance. In the UK insurance is only offered on a blackjack. Hence in the UK a counter’s edge must be about half of what it is under rules allowing insurance on any ace. Have I got this right?
According to the famed “Illustrious 18” table in Don Schlesinger’s “Blackjack Attack” insurance is the single most valuable hand to the counter, in terms of value gained by making count dependent strategy changes. The value of taking insurance, when the true count is +3 or more, adds 0.117% to the player’s overall advantage, based on the hi-low count, spreading 1 to 8. However this does not come close to half the total advantage from strategy changes. Looking only at the top 18 count dependent plays (the Illustrious 18), plus the top 4 count dependent surrenders (the Fab Four) the total value to the counter is 0.469%. So correct insurance accounts for only 25% of the value of strategy changes. A good counter will gain about another 1% by betting more in good counts. So taking away the insurance option reduces the total value of counting by only about 8%. In the UK it would be slightly less because you can still insure with a blackjack. The advantage figures are rough and depend on lots of things. The value of all surrender deviations is about the same of insurance deviations.
What is the exact house edge and basic strategy for Betfair’s "Zero Lounge" blackjack? Do their other games really have no house edge?
For the benefit of other readers, the blackjack rules are as follows.
- 8 decks
- Dealer stands on soft 17
- Dealer always peeks for blackjack
- Double on hard 8 to 11 only
- Double after split allowed
- Shuffle after every hand
- Aces may not be split. All other matching ranks may be split only once.
- Suited blackjack pays 2 to 1
- A 5-card 21 automatically wins and pays 2 to 1
I get a house edge of 0.02% under these rules. Following is the basic strategy.
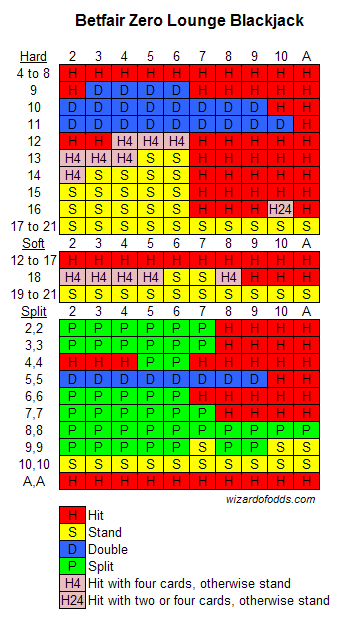
Regarding the other games, the 2.75% commission on the banker bet in baccarat results in a house edge of 0.03%. The roulette and video poker have zero house edge.
The bet limits are £5-£50 in blackjack, baccarat, and roulette, and the coinage is £1 in video poker, with a max bet of five coins.
I love the site; thanks for all the hard work. The blackjack survey is great and I notice that most casinos have more than one set of rules. Can I rightly assume that the better the rule set, the higher the table minimum at a given casino? For example, the lowest house edge at the Bellagio is quite good but does the table have $100 minimums?
Thank you, and you’re welcome. Yes, it is generally the case that the better the rules, the higher the minimum bet.
I was reading the Blackjack entry on Wikipedia, and it said that when blackjack was not that popular, casinos added a bonus payout of 10 to 1 for the ace of spades and any black jack, hence the name. It goes on to say that the bonus was quickly removed, but the name stuck. I was wondering what the house edge was with a 10-1 payout for that hand.
In a six-deck shoe, the probability of such a blackjack is 2 × (6/312) × (12/311) = 0.001484. I’m going to assume that if the dealer has a blackjack also, then the hand is a push. That said, the probability of the dealer not getting blackjack, given that the player did, is 1 - 2 × (23/310) × (95/309) = 0.954379. So the probability of winning such a blackjack is 0.001484 × 0.954379 = 0.001416. The value of an additional 8.5 units whenever that happened is worth 8.5* 0.001416 = 1.2039%. Assuming otherwise liberal Vegas Strip rules, with a house edge of 0.28%, the player edge with the 10 to 1 rule would be 0.92%.
I recently made a trip out to Vegas, where I came upon a game called the "World’s Most Liberal Blackjack" at the Las Vegas Club. In this game you are allowed to: double down with any 2, 3 or 4 card combination, split & re-split aces as often as you choose, split & re-split any pair as often as you like, surrender your first two cards for half of your original bet and any hand with six cards automatically wins. The caveat is blackjack pays even money unless it’s suited in which case it pays 2 to 1. Is this a better game than a 3 to 2 BJ with 6 decks and the dealer standing on a soft 17? Also, in this case, would it be beneficial to double down since the BJ only pays even money?
The house edge of this game is 1.30% or 1.33%, as shown in my survey of Las Vegas blackjack rules, depending on whether the number of decks is five or eight. The odds are better in ANY game where blackjack pays 3 to 2. If you were to play this game, which you shouldn’t, you should still always stand on blackjack. Personally, I think the "World’s Most Liberal Blackjack" claim on the marquee is false advertising.
The racinos in Pennsylvania recently added electronic blackjack tables. Apparently, to get them installed they had to work like a slot machine or video poker. Does this mean the results are predetermined when the cards get dealt? Also I do not know the rules, but do you know what is the house edge for this game?
The game you refer to is by Shufflemaster for their TMS-300 series of games. It is mathematically equivalent to a hand-dealt game. Conventional basic strategy should be used. In Pennsylvania, to meet gaming regulations, a separate shoe is used for each player, so one player’s actions do not affect other players. In all other states a single shoe is used. Shufflemaster tells me the following rules are common to all units.
7-card Charlie.
Double after split allowed.
Late surrender allowed.
Player may split only once.
Split aces get one card each.
In six-deck games the cards are shuffled after 2/3 shoe penetration. The player is not informed when the shuffle takes place. In single-deck game the cards are shuffled after every hand.
The following table shows the configurable rules and the house edge under each variation, assuming total-dependent basic strategy.
Shufflemaster TMS-300 Video Blackjack
| Number of Decks |
Blackjack Pays |
Soft 17 |
Hole Card |
House Edge |
| 6 | 3 to 2 | Stands | American | 0.39% |
| 6 | 3 to 2 | Stands | European | 0.50% |
| 6 | 3 to 2 | Hits | American | 0.59% |
| 6 | 3 to 2 | Hits | European | 0.69% |
| 1 | 6 to 5 | Stands | American | 1.25% |
The Majestic Star in Gary, Indiana, offers double-deck blackjack, but you can’t split aces. How does that affect the house? The other rules are double on 10 and 11 only, no double after split, split other pairs once, and dealer stands on S17.
Oy! Not being allowed to split aces costs the player 0.18%. Overall the house edge under these rules is 0.81%, based on total dependent basic strategy and a cut card game.
Bally Gaming has a single-deck, multi-hand, blackjack game. The player plays seven hands against a single dealer hand. There is an interesting rule in that if the game runs out of cards, all unbusted player hands automatically win. What is the probability of running out of cards? Can have suggest any strategy changes to run out the deck?
For the benefit of other readers, the full set of rules is:
- Single deck.
- Dealer stands on soft 17.
- Winning blackjack pays even money.
- Player may double any first two cards.
- No double after split.
- Player may resplit to four hands, including aces.
- No draw to split aces.
- No surrender.
- Six-card Charlie (player unbusted six cards automatically wins).
- Cards shuffled after every hand.
- If game runs out of cards, all unbusted player hands automatically win.
The house edge using total-dependent basic strategy is 2.13%. I ran a 7-player simulation, using total-dependent basic strategy, and the average number of cards used per round was 21.65, with a standard deviation of 2.72. In almost 190 million rounds played, the most cards ever used was 42, which happened 7 times.
It is my educated opinion that even with computer perfect composition-dependent strategy the player would still realistically never see the last card. You could cut down the house edge much more using composition-dependent strategy, according to all the cards seen as you go along. However bucking 2.13% house edge to start with, you’ll never get anywhere near break-even, regardless of how hard you try.
I’m a blackjack dealer from the great state of Oklahoma, where class 2 gaming became legal approximately 2 years ago. However, the state also legalized a tax for the Indian Nation that owns the casino, at $0.50 a hand on table games (except poker, there tax is slightly different). My question to you is, playing on a 6-deck blackjack table, where the dealer stands on soft 17, up to 4 splits with doubles, split aces up to 4 times with one card, blackjack pays 3-2 and no surrender what would the house edge be with playing an average bet of $10 a hand. Thank you.
I’m assuming the player must put up the 50 cents. My blackjack house edge calculator says the house edge under those rules, without the tax, is 0.36%. Add to that 0.5/10 = 5%. So the total house edge is 5.36%. In my opinion, players should refuse to play this game, on principle alone.
Here in Pennsylvania we have blackjack games, made by Shufflemaster, where the players use terminals to play against a video screen of a dealer. Technically, only "slots" are legal in Pennsylvania. I heard that the game was "retrofitted" to fit the definition of a slot. What does that mean? If this is just a glorified slot machine, do I really have any control over my fate?
Yes, you do. I’m told by Shufflemaster that to meet the definition of a slot machine, one player’s actions can not affect the other players, as is the case in live blackjack. To get around this law, each player and the dealer are dealt cards from a unique six-deck shoe. So, you are in control of your own fate, but not that of the other players or the dealer. I understand that the game is programmed with six-deck shoes. According to my simulations, using separate shoes for the player and dealer adds 0.06% to the house edge.
I absolutely love your site. I enjoy the strategies and probability discussions as much as, or more than, the actual gambling! I was playing six-deck Blackjack in a St. Louis casino recently. After playing a shoe, the cards were returned to the auto shuffler, which indicated a card was missing. The dealer proceeded to deal the next shoe while the floor person inspected the returned set of cards. Upon completion of this shoe, the missing card from the previous shoe (a king) was found in the un-dealt portion of the second shoe.
Assuming this King was the bottom card and was left in the shuffler, it would have been in play in this first shoe (the cut was in rear portion of the deck). How much of an additional advantage did the house gain on me with this mistake?
Thank you for the kind words. I’m going to assume the dealer hits a soft 17, and double after a split is allowed. According to table D17 in Blackjack Attack by Don Schlesinger, removing one ten per deck increases the house edge by 0.5512%. Dividing that by six, for the six-deck game, the effect is an increase in house edge of 0.09%.
Hollywood Park has their new blackjack rules up on their site. I’d be interested to see an analysis if you have the time.
It seems like every casino in LA County has different blackjack rules, and they change frequently. They are often complicated to analyze. I’m afraid I have adopted an unofficial policy to spend no more time on the bizarre blackjack scene in LA.
I was in Palace Station the other day and saw they had a few 7 to 5 double deck tables now. They may just be testing the idea out, but it could catch on, just like 6 to 5 did. So, you might want to include 7 to 5 in your rules variations.
Thanks, that is duly noted. Normally, the house edge under Palace Station rules (double deck, dealer hits soft 17, double after split, re-split aces) is 0.40%. This rule bumps that up to 0.86%. The following table shows the increase in house advantage due to this rule.
7 to 5 BJ Additional House Edge
| Decks | Increase |
| 1 | 0.46% |
| 2 | 0.46% |
| 4 | 0.45% |
| 6 | 0.45% |
| 8 | 0.45% |
I found an online casino with two interesting blackjack rules. The first is that a player 21 will push against a dealer blackjack. The second is that a blackjack tie pays 3 to 2. What is the effect on the house edge of these rules?
Based on six decks, I show a player 21 pushing against a blackjack lowers the house edge by 0.37%. A blackjack tie paying 3 to 2 lowers the house edge by 0.32%. No strategy changes are required.
What gain is there for a player when the house allows late surrender on a 6-deck shoe, when the house hits soft 17, and when the house stands on soft 17? What about an 8-deck shoe?
Answers to questions like that can be found using my house-edge calculator by changing a rule and noting the effect on the house edge. Normally I would make you do it, but I’m in a patient mood today, so here you go:
6 decks, dealer stands on soft 17: 0.0726%
8 decks, dealer stands on soft 17: 0.0758%
6 decks, dealer hits on soft 17: 0.0882%
8 decks, dealer hits on soft 17: 0.0916%
I play at a casino that allows unlimited re-splitting of cards in a six-deck black jack shoe, except for no re-splitting aces. In general, it must be beneficial to the player, but was wondering by how much and if there are points at which you stop splitting. I have found no information on this rule.
Unless you are counting cards, you should keep re-splitting as much as possible, up to the maximum 24 hands in a six-deck shoe. The value of infinite resplitting compared to a maximum of three times is very little. It depends on whether or not double after split is allowed, but either way, the value is well under 0.01%.
Most to all of our casinos here in OK require a blackjack player to ante $0.50 every hand. Obviously, this gives the house a huge (probably insurmountable) edge. The rules they play by are generally hit on 16, stand on soft 17, blackjack pays 3-2, no surrender, double after split. What effect does this have on house edge and is the only way to reduce that edge to increase your bet? I was estimating 10% (because you’re really betting $5.50 to only win $5). Is the math really that simple?
If you are wagering $5, not including the 50-cent fee, that increases the house edge by 9.09%! The general formula for the increase is c/(b+c), where b=bet, and c=commission. Assuming 60 hands an hour, the commission will cost you $30 an hour (ouch!).
For the benefit of other readers, the Oklahoma casinos are much like those in the Los Angeles area, where players take turns banking. If you can afford the risk of paying off all other wagers at the table, then by all means, do so. When it isn’t your turn to bank, don’t bet.
Do you have any information on video blackjack? Do the rules/payoffs vary, and where are the best games in Vegas?
I think your odds are best with the big Table Master units with big video screens housing attractive dealers. These are getting easier and easier to find, but I don’t know of any specific list of them. Your odds of finding them will be better in low-roller casinos. Some pay 3 to 2 on blackjack, and some only pay 6 to 5. An an example, the unit at the Riviera has the following rules:
- 6 decks (shuffled after four decks)
- Blackjack pays 3 to 2
- Dealer hits soft 17
- Double after split allowed
- Double on any two cards allowed
- Surrender allowed
- Split to two hands only
- Seven Card Charlie (un-busted hands of 7 cards automatically win)
- Bet range: $2-$200
The house edge under these rules is 0.68%. If you play an even-money game, the house edge will be 1.4% to 2.0%, depending on the other rules. Be sure to use a player card to earn whatever cash, free play, or comps the casino offers.
The picture below shows one of these products.

At the Borgata in Atlantic City, a $10.50 blackjack pays $16, since they don’t have quarters to pay you and always round up to the next 50 cents if you are owed a quarter. How does betting this amount affect the odds?
You’re getting paid 32 to 21 on a blackjack. That is an extra 1/42, or 2.38%. In a six-deck game, the probability of a winning blackjack is 4.53%. So, this is worth 2.38% × 4.53% = 0.11%, which isn’t bad. However, I think it is not a very elegant trick.
A local casino has a "special" blackjack table at which one can advance reserve the table for $20 for an hour of play. The table is a $5 minimum with standard blackjack rules except the house hits a soft 17. How lousy of a game is this, taking into account the nonrefundable reservation fee?
If we assume 70 hands per hour, a house edge of 0.64%, and a $5 bet, the cost of playing before the fee would be $5 × 70 × 0.0064 = $2.24. That $20 fee is pretty high in comparison. Considering you would bet $350 per hour, the total expected loss would be $22.24, for a house edge of $22.24/$350 = 6.35% (ouch!).
How does the house edge change in blackjack if you can only split aces?
It would depend on the other rules, but assuming six decks and double after a split being normally allowed, then the house edge would be increased by 0.39% only. If doubling after splitting is not otherwise normally allowed, then 0.24% only. This situation actually applies in the game Triple Shot, where I get 0.33%, due to it being a single-deck game. Keep in mind, when it comes to blackjack, such figures can be off by 0.03% or so, depending on how the analysis is done.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Resorts in Atlantic City introduced $2 blackjack tables that require the player to pay a 25¢ fee to play each hand. Here is an article about it. What is the house edge under this rule?
The standard Atlantic City rules are 6 or 8 decks, dealer stands on soft 17, double after split allowed, no surrender, no re-splitting aces, and the player may only split other pairs twice. However, Resorts also has some tables with those rules except the dealer hits a soft 17. Using my blackjack house edge calculator, and assuming 8 decks, the house edge is 0.46% if the dealer stands on a soft 17 and 0.67% if he hits. The general formula for the increase in the house edge if a nonrefundable fee must be paid per hand is f/(b+f), where f is the fee and b is the initial bet. In doing so, I define the house edge as the ratio of the expected loss to the sum of the bet and the fee. So, at a $2 bet, the increase in the house edge is 0.25/2.25 = 11.11%. At a $5 bet, the increase is 0.25/5.25 = 4.76%. I would assume they are going to have the dealer hit a soft 17 at these tables, making the overall house edge 11.78% at a $2 bet and 5.43% at a $5 bet. This is much worse than the 6 to 5 games or even money games they have in Vegas. Still, this isn’t as bad as the rule where a player loses on ties, which I saw in Finland.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I know what the chart says, but I can’t make myself split eights against a dealer 9, 10 or ace in blackjack. My question is what is this doing to the house edge?
Let’s assume six decks, the dealer stands on soft 17, and the player may re-split to up to four hands. The effect of each basic strategy change is the probability of the hand occurring and the cost of not making the correct play when it does. My blackjack appendix 9 shows both the probability of each hand and the expected value of each play. Assuming the player chooses to hit instead of split, the effect on the expected value of the game is:
Prob(8,8 vs A)×(EV(hit)-EV(split)) + Prob(8,8 vs 9)×(EV(hit)-EV(split)) + Prob(8,8 vs 10)×(EV(hit)-EV(split))
= 0.0003036 × (-0.513551 -(-0.364371)) + 0.0004404 × (-0.505707 -(-0.38995)) + 0.0016249 × (0.535361 -(-0. 475385))
= -0.019%.
So hitting 8,8 against a dealer 9, 10 or ace increases the house edge by 0.019%, or about one bet every 5,300 hands played. If the player surrenders instead of hitting, the effect drops to 0.013%. So, it is not a significant mistake. To put it in comparison, taking "even money" with a blackjack against a dealer ace increases the house edge by 0.014% in a six-deck game. If the player insures every blackjack and 20 (a common mistake), then the error cost jumps to 0.149%!
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
The Current Blackjack Newsletter blackjack rules on your Wizard of Vegas site indicate that at the Bighorn casino a blackjack pays 2 to 1, if at least 2 or more players at the table get a blackjack. Can you tell me the effect of that rule?
I show that rule is worth 0.10% per each additional player at the table, not counting yourself. According to my blackjack house edge calculator, the house edge is 0.48% before considering that rule, or the rule allowing doubling on three cards. Doubling three or more cards is worth 0.23%. To make an educated guess, let’s assume doubling on exactly three cards is worth 0.20%, lowering the house edge to 0.28%. Considering the 2-1 blackjack rule, the following is the house edge according to the total number of players, including yourself.
Bighorn House Edge
| Players | House Edge |
| 7 | -0.32% |
| 6 | -0.22% |
| 5 | -0.12% |
| 4 | -0.02% |
| 3 | 0.08% |
| 2 | 0.18% |
| 1 | 0.28% |
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
In the four casinos in Colombo, Sri Lanka they have the following blackjack rules:
- 6 decks
- Dealer does not take a hole card
- Player may "early" surrender, except against an ace
- Dealer stands on soft 17
- Player may double on any first two cards
- Double after split allowed
- Re-splitting aces allowed
- If dealer gets a blackjack, player will lose only his original bet
- Player may opt to win half his wager with any original five-card hand under 21
I show that combination of rules has a player advantage of 0.65%!
The last rule mentioned can also be found at the Pharaohs Palace in Macau, too. It is a breakeven game there, though, because of other bad rules, like doubling on 11 only. I have a strategy for the five-card half-win rule on my blackjack page at Wizard of Macau.
A local Connecticut casino is having a one-day promotion, in the middle of July, where the player can triple down in Blackjack. What would be the appropriate basic strategy and house edge?
I know about it. The Mohegan Sun is running a "triple down" promotion for 24 hours, starting at 6:00 AM on July 15. It is valid on all blackjack and Spanish 21 tables, and the maximum additional wager is $500. Information can be found on both the Mohegan Sun’s promotions page. The newsroom used to have the following statement, but it was removed:
Showing an eleven and looking to double down? On Thursday, July 15th, guests who play Spanish 21 or Blackjack will be eligible to triple down on their bet f.rom 6:00am on July 15th to 5:59am on July 16th. After a player receives their first two cards, they may make an additional wager up to triple the amount of the original wager. All tables will make tripling down available up to a $500.00 maximum bet. Standard double down rules apply.
The removed content indicates that the player may quadruple down, because the total wager would be four times as much as the initial wager. Maybe it was removed because it was a misprint.
I’m told in blackjack they use six decks, stand on a soft 17, allow surrender and double after a split, but don’t allow re-splitting aces. Normally the house edge under those rules would be 0.36%. I’m not sure if the player will be allowed to triple/quadruple after a split. Here is the player edge under various sets of rules:
- Player may triple down on first two cards, double down after split: 1.39%
- Player may triple down on first two cards, triple down after split: 1.59%
- Player may quadruple down on first two cards, double down after split: 3.20%
- Player may quadruple down on first two cards, quadruple down after split: 3.62%
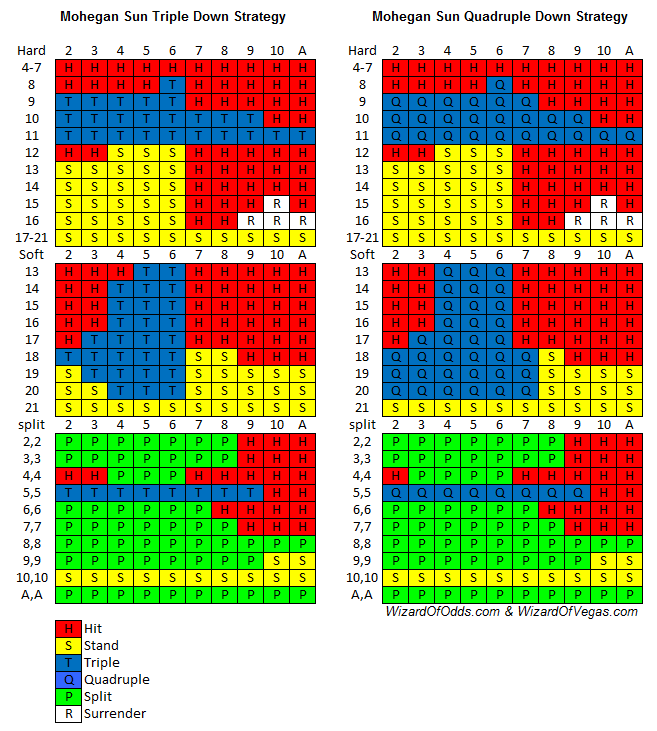
Resorts in Atlantic City charges a 25¢ fee to play blackjack for bets of $2 to $5. How does that affect the house edge?
In any game that charges a fee to play, which is common in the California card casinos, the increase in the house edge is f/(f+b), where f is the fee, and b is the bet. In this situation, I define the house edge as the ratio of the expected player loss to the sum of the bet and the fee. So, if your blackjack bet is $2, then the increase is 0.25/2.25 = 11.11%. If you bet $5 then the increase is 0.25/5.25 = 4.76%.
My advice is that if you can’t afford the minimum $10 to avoid the fee, then play video blackjack, or some other game.
There is an article about this at www.pressofatlanticcity.com.
A casino in Oklahoma is putting three jokers in a six-deck shoe of blackjack. How does that affect the odds?
Stanford Wong address jokers in blackjack in his book Basic Blackjack. There he says each joker per deck is worth 4.2% to the player. So half a joker per deck would be worth 2.1%. His book contains a strategy for what card to declare the joker as, according to your other card(s), and the dealer’s up card.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I heard of a casino where if the dealer busts then he assumes all players left standing won. The game is dealt face up, except double down cards are dealt face down. So if the double down card caused the player to bust, but the dealer also busted, then the player would win. The casino does this because it is paranoid about card counters, and doesn’t want players to see cards they think are irrelevant. What would be the correct basic strategy under this rule, and the house edge?
I’m going to assume six decks, dealer hits a soft 17, double after split, surrender, and re-splitting aces. If double for less is not allowed then I get a player edge of 4.9%. Here is that correct strategy. Obviously, this strategy may set off some red flags.
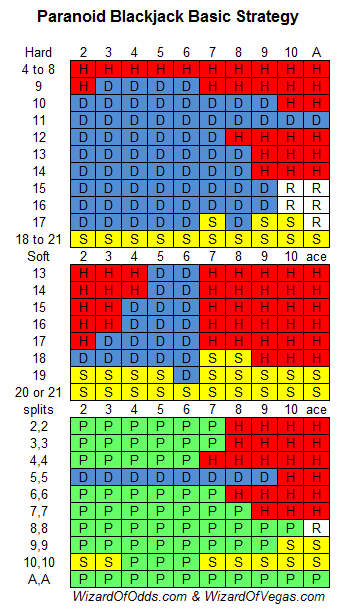
If double for less is allowed, then I get a maximum player edge of 9.4% with the following strategy. When doubling for less, bet as little extra as possible, preferably just one penny. My 9.4% figure assumes a tiny double down wager. In reality, most casinos require doubling with at least the table minimum.
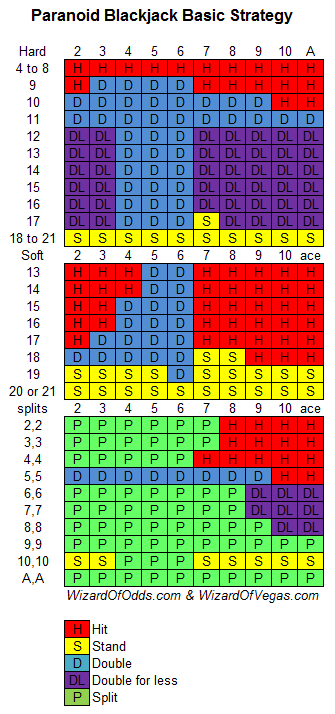
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I play at a casino that allows you to split pairs an unlimited number of times. What is the effect of this rule?
I show the value of infinite re-splitting, compared to splitting up to a maximum of four hands, is worth 0.05% if the rule applies to all pairs, including aces, and 0.02% if it does not include aces. This question was raised and discussed in the forum of my companion site Wizard of Vegas.




