Ask The Wizard #426
Suppose a serial numbers are numbered sequentially starting with 1. The maximum number in circulation is unknown. Given a random sampling of n numbers, what is the best estimate of the maximum serial number?
The way I like to think of the answer is to find the average gap between serial numbers. The way to calculate this is to take the maximum value and divide by the sample size. For example, if the largest item in your sample was 1,000 and you have a sample size of 5, then the average space is 1000/5=200. Then add that space to the maximum observation to get the estimated highest number. In this example, 1000+200 = 1200.
The usual formula given that arrives at the same number is M*(k+1)/k, where M = Maximum value and k=number of observations. In our example, this gives 1000*(6/5) = 1200.
ABCD is a square with side length 10. Inside it are inscribed a semicircle and quarter-circle, as shown in the following diagram.
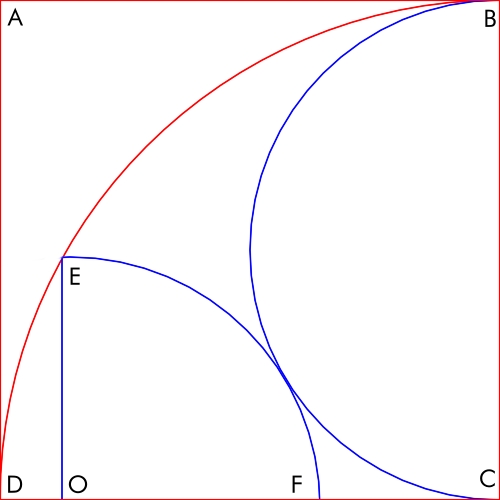
What is the length of OE?
Consider the following diagram.
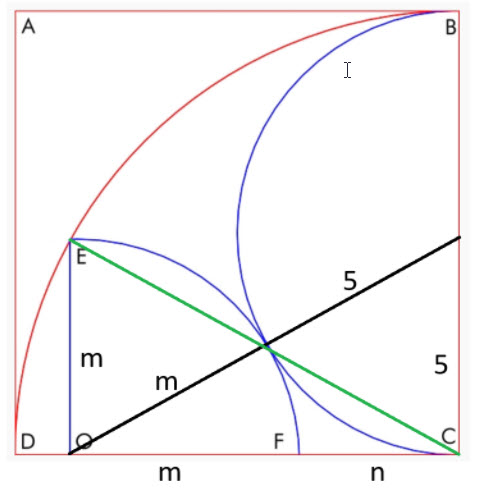
Here we have two right triangles, one with the green hypotenuse and the other black. Let's set up the two Pythagorean equations:
- Green hypotenuse: m2 + (m+n)2 = 102
- black hypotenuse: 52 + (m+n)2 = (m+5)2
Let's rearrange the first equation to (m+n)2 = 102 - m2
Let's substitute that value for (m+n)2 into the second equation:
52 + 102 - m2 = (m+5)2
25 + 100 - m2 = m2 + 10m + 25
2m2 + 10m - 100 = 0
m2 + 5m - 50 = 0
Using the Pythagorean formula to solve for m:
m = (-5 +/- sqrt(25 + 200))/2
m = 5 or -10. 5 is the only reasonable answer.
This question is asked and discussed in my forum at Wizard of Vegas.
A large number of students are taking a 10-question test. Every question is true or false. What is the maximum number of students that can be taking the test such that any two tests will differ from each other by at least two questions?
Take one test as what we'll call the key test.
Group 1 = The number of ways other tests can be different by exactly 2 questions from the key test is combin(10,2)=45.
I'm not going to calculate the number of ways to be different by 3 from the key test, because some of those ways will match 9 out of 10 to a test from group 1.
Group 2 = The number of ways other tests can be different by exactly 4 questions from the key test is combin(10,4)=210. Any of these will also differ from any test in group 1 by at least 2.
Repeating this logic...
- Group 3 = The number of ways other tests can be different by exactly 6 questions from the key test is combin(10,6)=210.
- Group 4 = The number of ways other tests can be different by exactly 8 questions from the key test is combin(10,8)=45.
- Group 5 = The number of ways other tests can be different by exactly 10 questions from the key test is combin(10,10)=1.
So, the answer is the sum of groups 1 to 5 plus one for the key test = 1+45+210+210+45+1 = 512.
That number is the same as 2^9. Could that be a coincidence? No!
The number of ways to draw an odd number of items from a larger groups is the same as the number of ways to draw an even number. This is because every item in the large group can either be picked or not picked. There are 2^n combinations of each member being picked or not picked in a group of n items. If you were to list them systematically in binary order, the number of combinations chosen would alternate between even and odd. The total number if the group is 2^n, which is itself even, so half of 2^n will be even.
So, the sum of groups 1 to 5 is the number of ways to choose an even number of questions that match the key test. This will be equal to the number of ways to choose an odd number of questions that match the key test. The total number of ways to match or not match the key test is 2^10 = 1024. Half of those will match an even number of times. So, the answer is 1024/2 = 512.
This question is asked and discussed in my forum at Wizard of Vegas.


