WOO logo

Wizard Recommends

Ask The Wizard #422

For the sake of argument, assuming a blackjack game with an infinite number of decks, infinite re-splitting is allowed, and the player will split any pair. What is the probability of any given number of final hands the player plays out?

anonymous

The probability of re-splitting to n hands is (combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n . For more information about that first term, which I needed some help with, look up Catalan numbers.

The following table shows the probability of 1 to 20 final hands. The seconds column is the number of "trees," which is the Catalan number in the expression above.

 

Hands Trees Probability
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.0000000000002

 

I hear there are an infinite number of Pythagorean triples. Is there any formulaic way of finding them?

anonymous

Yes, there are an infinite number of unique Pythagorean triples! For those who are not familiar with the term, they are right triangles where each side is an integer. 3-4-5 is the most famous one. To get a unique (in other words non-reducible) set Pythagorean triple chose any integer values for a and b where a < b and one is odd and one is even.

  • Leg 1 = b2 - a2
  • Leg 2 = 2ab
  • Hypotenuse = a2 + b2

 

The following table shows all non-reducible Pythagorean triples where all sides are 101 or less.

a,b Leg 1 Leg 2 Hypotenuse
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

 

What is the probability of rolling every total, with two dice, other than a seven, at least twice, before rolling a seven?

Garrison

The trick to questions like this is that the probability is the same if the time between rolls follows an exponential distribution with a mean of 1. In this case, it can be given with the following formula.

 

 

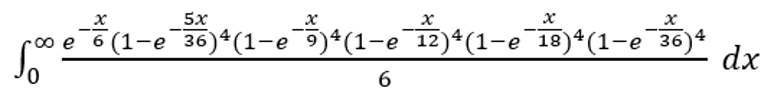
To put it in text form: exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6

For solving such integrals, I recommend this Integral Calculator.

The answer comes to 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848.