Ask The Wizard #405
x2 - 3 = sqrt(x+3). Solve for x.
Let y = both expressions. So, we have:
- y = x^2 - 3
- y = sqrt(x+3)
Note the 3 in both expressions. Let's express both equations with a 3 on one side. First we have:
3 = x^2 - y
Next, let's square the second equation above:
y^2 = x+3
3 = y^2 - x
Let's equate both expressions for 3:
x^2 - y = y^2 - x
Let's rearrange:
x^2 - y^2 + x - y = 0
(x+y)(x-y) + x - y = 0
(x-y)(x+y+1) = 0
First let's examine x-y = 0:
x-y = 0
Let's substitute y = x^2 - 3 for y.
x - (x^2 - 3) = 0
x^2 - x - 3 = 0
Using the Pythagorean formula:
x = (1 +/- sqrt(1 + 12)/2
x = (1 + sqrt(13)/2 & x = (1 - sqrt(13)/2
Second, let's examine x+y+1 = 0:
Let's substitute y = x^2 - 3 for y.
x + (x^2 - 3) + 1 = 0
x + x^2 - 3 + 1 = 0
x^2 + x - 2 = 0
Using the Pythagorean formula:
x = (-1 +/- sqrt(1 + 8)/2
x = (-1 +/- 3)/2
x = 1, x = -2
So, our four answers are:
- x = 1
- x = -2
- x = (1 + sqrt(13)/2 =~ 2.302776
- x = (1 - sqrt(13)/2 =~ -1.302776
I would like to thank the YouTube video Solving x^2-3=sqrt(x+3) by SyberMath for this method to solve this one. Jump to the 6:28 point for this method.
A point outside of a circle of radius 1 can see 1/3 of the circumference. How far away is the point?
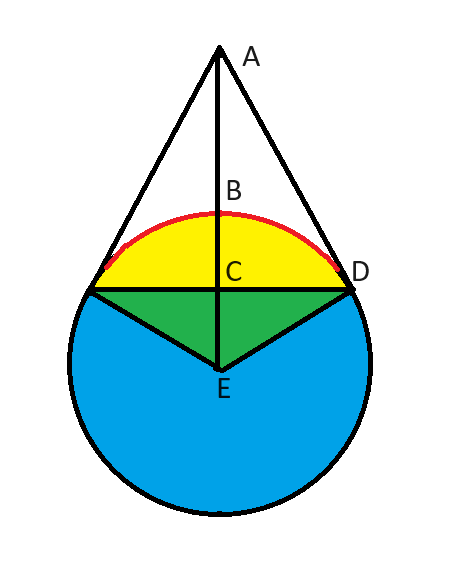
Consider the triangle ADE. We know:
- Angle ADE is 90 degrees, because AD is tangent to the circle.
- Angle AED is 60 degrees, because the green triangle angle at E is 120 degrees (1/3 of the whole 360).
- Angle EAD must be the other 30 degrees of triangle ADE.
This is the classic 30-60-90 triangle. We all should know the sides of said triangle are proportional to 1, 2, and sqrt(3).
In this case ED = 1, as given in the question. AE is twice that distance, or 2.
2 gives is the distance from the point to the center of the circle. We are asked the distance from the point to the closest point on the circle. So we subtract the radius. Thus, the answer is 2-1 = 1.
Bob and Tom are walking across a train bridge and are 1/3 of the way from your starting point. Then they hear a train coming from behind them. Both can run at a speed of 5 miles per hour. Bob turns back and Tom run forward. Both miss the train by less than a second. How fast was the train?
Remember distance = rate * time, which we will express as d = r*t
Rewriting that: t = d/r.
The time is the same in both Bob and the train meeting at the beginning of the bridge:
Let's let:
- x = distance between the train initially and the beginning of the bridge.
- r = rate of speed of the train
First, let's look at Bob, who runs back. Let's express t for both Bob and the train to meet at the beginning of the bridge:
Bob: t = (1/3)/5
Train: t = x/r
Equating the two expressions for t:
(1/3)/5 = x/rr/3 = 5x
r = 15x
Second, let's look at Tom, who runs ahead. Let's express t for both Tom and the train to meet at the beginning of the bridge:
Tom: t = (2/3)/5
Train: t = (1+x)/r
Equating the two expressions for t:
(2/3)/5 = (1+x)/r
2r/3 = 5(1+x)
2r = 15(1+x)
2r = 15 + 15x
At this point we have:
- r = 15x
- 2r = 15 + 15x
Let's substitute the expression for r in the first equation into the second:
30x = 15 + 15x
15x = 15
x = 1
Recall, r = 15x.
So, the speed of the train is 15*1 = 15 mph.




