Ask The Wizard #365
I hear the minimum taxable slot machine jackpot has been increased from $1,200 to $5,000. Is this true?
No.
A bill has been introduced to do just that. However, most bills go nowhere and never even get voted on, so slot players should not get their hopes up.
Personally, if I had a vote in the matter I would vote YES enthusiastically. The current $1,200 limit has not been increased since 1977. According to the American Institute or Economic Research, $1,200 in 1977 would have been worth $5,336 in 2021. I could easily make an argument against all taxation of gambling winnings. However, I know that ship won't float, so the least we can do is recalibrate the minimum taxable jackpot to inflation, which should have been done all along.
For more information, please read Bill would raise slot jackpot tax report threshold to $5,000 at the Las Vegas Sun.
There is a square of side length 1. Each corner of the square is the center of a circle of radius one. What is the area of the red region, where all four circles overlap?

0.3151467436277204526267681195872952611229178793146546456025078846506724518532
696291281987550234571136517565540890207325190613364415179082650967976239484533
906220014689983405916338783947732316433868623061639270583186549287254862947423
40423083863353504721515...
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
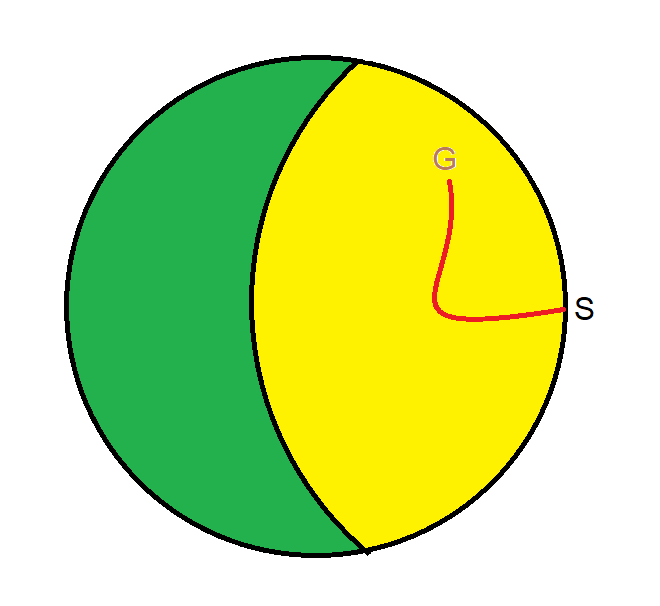
A grassy field is in the shape of a circle of radius 100m and is enclosed by a circular fence. A goat is attached by a chain to a hook, at a fixed point on the fence. To stop the goat getting too fat, the farmer wants to make sure that it can only reach half of the grass in the field. How long should the chain be?
By way of illustration, the circle represents the grassy field. The S represents where the chain is staked on the edge of the field. The yellow portion of the circle is where the goat can reach. The green area is beyond the reach of the chain. The goal is to make the chain the right distance so the green and yellow portions are equal.
Please refer to the following diagram in solving this problem.
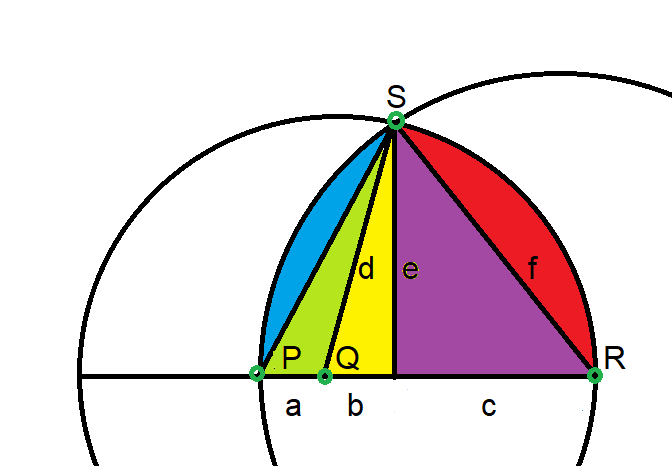
The point Q is the center of the grassy circle. The goat's chain is staked to point R. The goat can reach all the colored regions, including their mirror image below the line PR.
You're given that the radius of the grassy circle is 100, so b+c = d = 100.
The way I'm going to solve this is to define everything in terms of b. Then I'll play around with b until I achieve the desired result where the goat can eat half the grass.
Let's start by solving for e in term of b. Looking at triangle with sides b, d, and e and using the Pythagorean formula:
b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = sqrt(10000 - b^2)
Next, let's solf for f in terms of b. Remember, we already know b+c=100, so c=100-b. Using Pythagoras:
c^2 + e^2 = f^2
(100-b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100*(200 - 2b)
f = 10*sqrt(200-2b)
Next, let's find the area of triangle QRS:
QRS = (1/2)*100*e = 50*sqrt(10000 - b^2)
Next, let's find the area of the slice of the grassy as cut out by the angle SQR:
tan(SQR) = e/b = sqrt(10000-b^2)/b.
slice SQR = atan(sqrt(10000-b^2)/b)
The red area equals the slice SQR minus traingle QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).
Next, let's find the blue + green + yellow + purple area. To do this, we need to find the angle QRS.
tan(QRS) = e/c = sqrt(10000-b^2)/(100-b)
angle QRS = atan(sqrt(10000-b^2)/(100-b)).
Add to that the red area and we have half the total area the goat can eat:
atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).
Double that, for the part below line PR to get the total area:
2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).
The total area of the grassy region is 10,000*pi.
Now, just play around with b until you get an area the goat can eat equal to 5,000*pi. The goalseek function in Excel is great for problems like this. How anyone accomplished anything before spreadsheets, I have no idea.
Using this method, you will find that b = 32.867402.
From there we can get f = length of the chain = 115.8728598 meters.
This question is asked and discussed in my forum at Wizard of Vegas.
What are the frequent two-letter combinations at the beginning and ending of five-letter words?
You must be asking because you enjoy Wordle. My answer is based on this list of 2,315 possible Wordle answers.
The following are the most common combinations of the FIRST two letters.
First Two Letters
| Count | First Two Letters |
|---|---|
| 65 | ST |
| 52 | SH |
| 45 | CR,SP |
| 40 | CH |
| 38 | GR |
| 36 | FL,RE,TR |
| 35 | BR |
| 34 | MA |
| 32 | BL,CA |
| 31 | CL |
| 29 | CO,DR,MO,SC |
| 28 | DE,SL |
| 26 | BE,PR |
| 25 | PA |
| 24 | BA,TH |
| 23 | QU,RA,SA,SW,TA |
| 22 | AL,BO |
| 21 | FI,FR,LE,TO |
| 20 | BU,RO |
| 19 | HA,LO,PL |
| 18 | LA,PI,SN,UN,WH |
| 17 | DI,FO,HO,PO |
| 16 | FE,GL,GU,ME,PE,VI,WO |
| 15 | DO,GA,MI,PU,RI,SM,TE,WI |
| 14 | AB,FA,IN,LI,SE,SO |
| 13 | AN,BI,GO,HE,SI,SU,WA |
| 12 | AR,MU,TI,WR |
| 11 | AM,HU,LU |
| 10 | AD,AG,EL,EN,EX,FU,KN,NO,VA |
| 9 | CU,DA,DU,RU,SK,TW,VO,WE |
| 8 | AP,JU,NA,TU |
| 7 | AW,EA,GI,NE,NI,VE |
| 6 | AS,CI |
| 5 | AF,EM,ER,EV,GE,HI,ID,JO,OU,OV,US |
| 4 | AC,AU,AV,ET,HY,IM,JE,LY,OC,OP,PH |
| 3 | AT,AX,CE,CY,DW,KA,KI,NU,OF,OL,OR,SQ |
Not appearing on the list are these combinations that occurred only one or two times.
- Two times: AI,ED,EP,EQ,ES,GH,GN,IC,IR,IS,JA,NY,OD,OM,ON,OT,OW,RH,SY,UL,UP,UR,UT,YE,YO,ZE
- One time: AH,AO,AZ,BY,DY,EB,EC,EE,EG,EI,EJ,EK,EY,FJ,GY,IG,IL,IO,IT,IV,JI,KE,KH,KO,KR,LL,MY,OA,OB,OX,OZ,PS,PY,TY,UD,UM,VY,YA,YI,ZO
The following are the most common combinations of the LAST two letters.
Last Two Letters
| Count | Last Two Letters |
|---|---|
| 141 | ER |
| 58 | CH |
| 56 | LY |
| 52 | SE |
| 50 | AL |
| 47 | CK |
| 46 | TY |
| 39 | TE |
| 38 | DY,EL,GE,NG |
| 37 | NT,VE |
| 36 | ST,TH |
| 35 | LE |
| 34 | EN,OR |
| 33 | RY |
| 31 | KY |
| 30 | CE |
| 29 | ET |
| 28 | DE,NK |
| 27 | IC,NE,SH |
| 26 | ON,RE |
| 25 | ID,LL |
| 23 | ED,IT,NY |
| 22 | IN,ND |
| 21 | RT,SS |
| 20 | AR |
| 19 | IL,KE,ME,MP,SY,UT |
| 17 | LT |
| 16 | AT,PY |
| 15 | AN,UE |
| 14 | PE,RD,WN |
| 13 | AD,AY,EY,FF,MY,OT,RN |
| 12 | AK,GY,US |
| 11 | HT,LD,MA,ZE |
| 10 | EE,FT,PT,RA |
| 9 | CT,FY,GH,GO,OM,RK,UR |
| 8 | BY,OP,OW,WL |
| 7 | EP,HY,IE,IR,PH,TA,TO,UM,ZY |
| 6 | AM,BE,EW,HE,IO,OY,RM,RO |
| 5 | BO,CY,IA,LA,NA,OD,OL,RL,SK,UL,VY |
| 4 | AP,EF,EM,GN,IM,IP,LK,MB,OK,RP,UD,UP |
| 3 | AC,AW,DO,EK,EO,FE,GA,KA,LM,OF,RF,SM,SO,SP,TZ |
Not appearing on the list are these combinations that occurred only one or two times.
- Two times: AB,AX,BA,BI,CA,EX,HA,IF,IX,LO,LP,NO,OO,OS,OX,PO,UB,UG,UN,VA,VO,WY,XY,ZA
- One time: AE,AH,AO,AZ,BT,CO,EA,GI,HI,HO,IB,IG,II,IK,IS,JA,JO,KI,KO,LF,LI,MI,MO,OA,OB,OC,OE,OU,PA,RB,RH,SA,SI,TI,UI,WD,XT,YL,YP,YR




