Ask The Wizard #323
Is this parlay card any good?

In step one, you have to bet either way against the spread in an NFL game. At the time you asked this question (Jan. 2, 2020), the Vikings were a 7.5-point underdog. According to my NFL alternate point spread calculator, the probability of the the Vikings +8.5 winning that side is 52.22%.
For all the other games, I looked at the going money lines, subtracted out the juice, to get at a probability of winning. That said, the following table shows the probability of each leg winning.
William Hill Parlay Card
| Leg | Fair Wine | Prob. Win |
|---|---|---|
| Saints -8.5 | -7.5 | 47.78% |
| Vikings +8.5 | 8.5 | 52.22% |
| Hou | -135 | 57.45% |
| Bills | 135 | 42.55% |
| Patriots | -205 | 67.21% |
| Titans | 205 | 32.79% |
| Sea | -118 | 54.13% |
| Phil | 118 | 45.87% |
| LSU | -200 | 66.67% |
| Clemson | 200 | 33.33% |
| AFC | -130 | 56.52% |
| NFC | 130 | 43.48% |
The two picks with the best chance of winning in step 1 are the Patriots and LSU. Here is the probability of my recommded picks winning:
- Vikings +8.5 — 52.22%
- Patriots — 67.21%
- LSU — 66.67%
The product of these probabilities is 23.40%. Getting 4 for 1 results in a return of 4 × 23.40% = 93.60%. In other words, the house edge is 6.40%. So, I'd leave this one alone.
I'm thinking of creating a side bet for "push 22" blackjack variants that would pay 11 to 1 if the dealer busted with 22. What would be the odds?
I'm thinking of creating a side bet for "push 22" blackjack variants that would win if the dealer busted with 22. What odds should it pay and what would be the house edge?
Assuming the dealer always drew out his hand (even if every player already busted), then I show a probability of busting on 22 of 7.88% if the dealer stands on soft 17 and 8.00% if he hits a soft 17.
Assuming the dealer hits a soft 17, at a win of 11 to 1, the house edge would be 4.04%. At 10 to 1, it jumps to 12.04%.
I should warn you and advise players that this would be countable (shut up Wiz!).
Amy and Bob have a contest to be the first to win four flips of a fair coin. Amy wish to bet $8,000 on herself to win the contest. However, she may bet only one flip at a time. All bets pay even money. How can she structure her bets so that she wins $8,000 if she wins the entire series and loses $8,000 if Bob does.
Click the button below for the answer.
There are 16 possible mid-series states. The following table shows the bet Amy should make at each one and her balance before the bet following this strategy.
Answer
| Amy | Bob | Balance | Bet |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
Click the button below for the solution.
Let:
- a = Amy wins
- b = Bob wins
- w = Amy's net win so far in series
- f(a,b,w) = Amy's bet size next game
In puzzles like this, it is generally good strategy to start and the end and work your way to the beginning. That said, it is easy to see that:
f(3,3,0) = 8,000
In this situation, the 7th game is "winner take all." Amy should have winnings of 0 and bet 8,000 on the last flip, which will give her an 8,000 win if she wins the flip and a loss of 8,000 otherwise.
Going back a step, what if she has 3 wins and Bob has 2. If she wins the next flip, she wins the whole game. If she loses, she will be at a 3-3 score. We from f(3,3,0) she should have 0 if the score is 3,3. So, we need for her to have 8,000 if she wins the next flip and 0 otherwise. What will get here there is a net win in the middle of 4,000 and a bet of the same amount. So:
f(3,2,4000)=4,000
Going back another step, what if she has 3 wins and Bob has 1. If she wins the next flip, she wins the whole game. If she loses, she will be at a 3-2 score. We from f(3,2,4000) she should have 4,000 if the score is 3,2. So, we need for her to have 8,000 if she wins the next flip and 4,000 otherwise. What will get here there is a net win in the middle [(4,000+8,000)/2=6,000] and a bet of half the distance between those two goals, [(8000-4000)/2 = 2000]. So:
f(3,1,6000) = 2,000
Going back another step, what if she has 3 wins and Bob has 0. If she wins the next flip, she wins the whole game. If she loses, she will be at a 3-1 score. We from f(3,1,6000) she should have 6,000 if the score is 3,1. So, we need for her to have 8,000 if she wins the next flip and 6,000 otherwise. What will get here there is a net win in the middle [(6,000+8,000)/2=7,000] and a bet of half the distance between those two goals, [(8000-4000)/2 = 2000]. So:
f(3,0,7000) = 1,000
It is hopefully obvious that Amy should have a net win of 0 if the score is ever tied. In any tied scenario, her probability of winning the whole series will be 50%. With balanced goals of a win/loss of 8,000 in either case, she needs to bet at 0 or she will have a chance of not hitting either ending goal.
Next, if Amy is ever behind in the series, her net win should be -1 times the net win if she were ahead by the same score. For example, consider a score of Amy 2 - Bob 3 (or 2-3). If she loses the next flip, she loses the whole game. If she wins, she will be at a 3-3 score. We from f(3,3,0) she should have 0 if the score is 3,3. So, we need for her to have 0 if she wins the next flip and -8000 otherwise. What will get here there is a net loss in the middle of 4,000 and a bet of the same amount. So:
f(2,3,-4000)=4,000
By the same logic:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
Next, what should be Amy's bet if the score is 2-2? If she wins the flip, the score will be 3-2. From above, we see she need to have a net win of 4,000 with that score. We also see if she is down 2-3, we need her to have a net loss of 4,000. Thus, she needs to bet 4,000:
f(2,2,0) = 4,000
Going back a step from there, what if the score is 2-1? We have established she needs to have a net win of 6,000 if she wins the next flip (score of 3-1) and a net win of 0 if she loses (score of 2-2). What will get here there is a net win in the middle [(6,000+0)/2=3,000] and a bet of half the distance between those two goals, [(6,000-0)/2 = 3,000]. So:
f(2,1,3000) = 3000
Going back another step from there, what if she has 2 wins and Bob has 0. If she wins the next flip, the score will be 3-0. If she loses, it will be 2-1. She should have a net win of 7000 at 3-0 and 3000 at 2-1. What will get here there from a score of 2-0 is a net win in the middle [(7,000+3,000)/2=5,000] and a bet of half the distance between those two goals, [(7000-3000)/2 = 2,000]. So:
f(2,0,5000) = 2000
By flipping those scores where Alice has two wins and Bob has less, we also know:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
As explained before, Amy's net win should be 0 if the series is balanced, so at a score of 1-1 her net win should be 0. At a score of 2-1 she needs to be up 2,000 and at 1-2 she needs to be down 2,000. Thus, at a tied score of 1-1 she should bet 2,000, or:
f(1,1,0) = 2,000
What if Amy is up 1-0? We have established she needs to be up 5,000 at 2,0. At 1-1 she needs to be even. What will get here there from a score of 1-0 is a net win in the middle [(5,000+0)/2=2,500] and a bet of half the distance between those two goals, [(5000-0)/2 = 2,500]. So:
f(1,0,2500) = 2,500
By flipping the score to 0-1:
f(0,1,-2500) = 2,500
So, finally, we're at the first game at a score of 0-0. We need Amy to be up 2,500 if she wins the next flip and down 2,500 if she loses it. Thus, a bet of 2,500 will get us there. Or:
f(0,0,0) = 2,500
This question is raised and discussed in my forum at Wizard of Vegas.
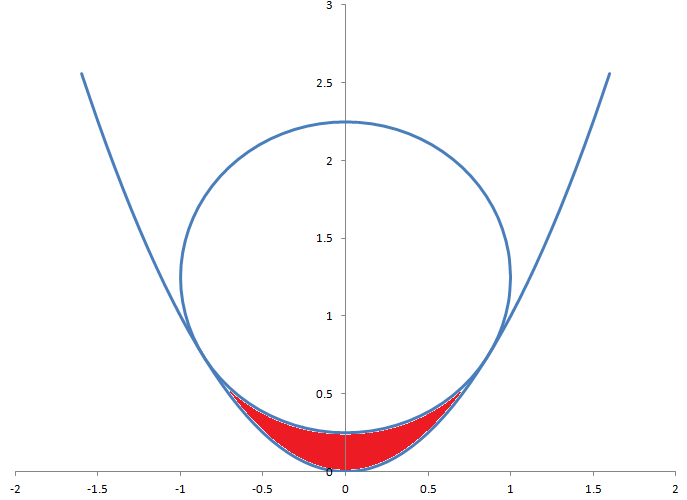
A circle of radius 1 is tangent to a parabola of equation y=x2. What is the area of the region in red, between the circle and parabola?
Click the button below for the answer.
Here is my solution. (PDF)
This question is asked and discussed in my forum at Wizard of Vegas.
I got this problem from Presh Talwalker of Mind Your Decisions.




