Ask The Wizard #318
What is the best strategy to play the Race Game on the Price is Right, assuming the player has no idea of the prices of the prizes?
For the benefit of readers who aren't familiar with the game, here is a video of it.
I submit that the following strategy results in a minimum average number of turns. There are many strategies that would tie it, but I don't think any can beat it.
To use the strategy, label the four price tags as 1, 2, 3, and 4. Place them on the four prizes according to the history of how many you got right in the past, starting with the first turn on the left.
Race Game Strategy
| History | Prize 1 | Prize 2 | Prize 3 | Prize 4 |
|---|---|---|---|---|
| None | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
The next table shows the probability it will take 1 to 5 turns of the 24 possible ways to arrange the four price tags.
Turns Required
| Turns | Number | Probability |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| Total | 24 | 100.00% |
Taking the dot product, the average number of turns needed, under this strategy, is 3.29167.
This question is asked and discussed in my forum at Wizard of Vegas.
On the September 18, 2019 episode of Jeopardy there was a category titled "Describe the Casino Game." One of the clues was "Dressed and playing to the 9's; Banker's hours; What brings you to Monaco, Mr. Bond?"

The answer provided was "baccarat," which was judged as being correct. Wasn't Bond playing chemin de fer?
Yes, indeed Bond was playing Chemin de fer, not baccarat. As a reminder, the main differences are:
- The turn to bank rotates around the table. The banking player automatically assumes the Banker* hand.
- Both Player* and Banker have free will to draw a third card, as long as neither has a two-card natural 8 or 9.
Note:
As usual, when writing about baccarat or chemin de fer, I capitalize the names of the bets, to avoid confusion with the players playing the game.
That said, the first such scene is in the Dr. No clip below, where not only does the bank rotate, player's have free will in the third card, but Bond actually refers to the game verbally as "chemin de fer" in the 2:11 point in the video:
The next video shows three chemin de fer scenes from three different movies.
Here are the starting points of each scene:
- 2:09 — Thunderball
- 4:19 — On Her Majesty's Secret Service
- 7:30 — For Your Eyes Only
In all three we see the players banking and free will in the third card decision, especially in For Your Eyes Only, where the odds are discussed.
Finally, below is the scene from Goldeneye.
Here we again see the turn to bank going back and forth and free will in drawing a third card. However, the female character does refer to the game as "baccarat" at the 0:45 point. I would file this under "character error."
In closing, there can be no doubt Bond was playing chemin de fer in every movie. Technically, I think the judges were incorrect to accept "baccarat" as a correct answer. However, I don't blame them. Even by Jeopardy standards, expecting the average player to know baccarat from chemin de fer would be too much. As shown by accepting an answer of "The Mooch," in lieu of Anthony Scaramucci, shows they are getting more lenient.
This question is asked and discussed in my forum at Wizard of Vegas.
As asked in the movie Mean Girls, what is:
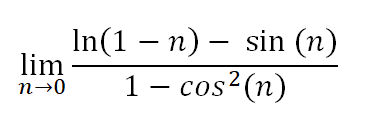
Let's start by looking at a graph of n (x-axis) by f(n) (y-axis).
As you can see, the limit approaches ∞ from the left and -∞ from the right. Since it doesn't converse to the same place from both sides, there is no limit.
However, let's answer the question without graphing. L'Hôpital's rule says that if the limit of f(x)/g(x) = 0/0, then lim f(x)/g(x) = lim f'(x)/g'(x). So, let's solve for f'(x) and g'(x).
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos2(n)) d/dn = sin2(n) d/dn
Let's use the product rule to solve for sin2(n) d/dn
sin2(n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n).
Next, let's solve for f'(n) and g'(n) at n = 0.
f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sin(0)cos(0) = 0
So, f'(0)/g'(0) = -2/0 = -∞. Thus, the limit of the original function doesn't exist.

I would like to compliment the writers of Mean Girls for getting the math in this movie perfect. Even serious mathematical movies, like Good Will Hunting, often completely blow the math.