Ask The Wizard #313
What is the variance in Cleopatra Keno??
As a reminder to our other readers, Cleopatra Keno plays like conventional keno, except if the last ball drawn matches one of the player's picks AND results in a win, then the player will also win 12 free games with a 2x multiplier. Free games do not earn more free games.
You didn't specify the number of picks or pay table, so let's use the 3-10-56-180-1000 pick-8 pay table, as an example. First, let calculate the return.
The number of ways to catch x balls out of y in keno is the number of ways to pick x balls out of 20 and y-x out of 60. This equals combin(20,x)*combin(60,y-x), to put it in Excel terms. As a further reminder, combin(x,y) = x!/(y!*(x-y)!). Finally x! = 1*2*3*...*x.
With that review out of the way, here is the return table for that pay table. The right column shows the expected square of the win, which we'll need later.
Pick 8 Keno
| Event | Pays | Combinations | Probability | Return | Return^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| Total | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
Next, let's calculate the average bonus. We can see from the table above that the average win, not counting the bonus, is 0.593301. In the bonus, the player gets 12 doubled free spins. Thus, the expected win from the bonus is 2×12×0.593301 = 14.239212.
Next, let's calculate the probability of winning the bonus. If the player catches four numbers, the probability the 20th ball is one of those 4 is 4/20. In general, if the player catches c, then the probability that the 20th ball contributed to the win is c/20.
The formula for winning the bonus is prob(catch 4)*(4/20) + prob(catch 5)*(5/20) + prob(catch 6)*(6/20) + prob(catch 7)*(7/20) + prob(catch 8)*(8/20). We know the probability of any given win from the return table above. So, the probability of winning the bonus is:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644.
With the probability of winning the bonus and the average bonus win, we can calculate the return from the bonus as 0.021644 × 14.239212 = 0.308198.
Not that we need to know, but the overall return for the game is the return from the base game plus the return from the bonus, which equals 0.593301 + 0.308198 = 0.901498.
Now, let's start getting into the actual variance. As a reminder, a general formula about variance is:
var(x + y) = var(x) + var(y) + 2*cov(x,y), where var stands for variance and cov stands for covariance. In this case of this game:
Total variance = var(base game) + var(bonus) + 2*cov(base game and bonus).
The fundamental formula for the variance is the E(x^2) - [E(x)]^2. In other words, the expected square of the win less the expected win squared.
That said, let's start with the variance of the base game. Remember when I said before when we would need that expected win squared from the first table. The lower right cell of that first table shows us the expected win squared is 19.530214. We already know the expected win is 0.593301. Thus, the variance of the base game is 19.530214 - 0.5933012 = 19.178208.
Next, let's calculate the variance of the bonus (assuming it was already hit). For that, recall that:
var(ax) = a2x, where a is a constant.
Also recall that the variance of n random variables x is nx.
That said, if x is the base win in a bonus game, then the variance of the whole bonus is 22 × 12 × x. We know from above the variance of a single spin in the base game, not counting the bonus, equals 19.178208. So, the variance of the bonus, given a bonus was already hit, is 22 × 12 × 19.178208 = 920.554000.
However, what we need to know is the variance of the bonus before the first ball is drawn, including the possibility the bonus won't be won at all. No, we can't just multiply the variance of the bonus by the probability of winning it. Instead, recall that var(x) = E(x^2) - [E(x)]^2. Let's rearrange that to:
E(x^2) = var(x) + [E(x)]^2
We know the mean and variance of the bonus, so the expected win squared in the bonus is 920.554000 + 19.1782082 = 1123.309169.
So, the expected square of the win from the bonus, before the first ball is drawn is the prob(bonus) × E(x^2) = 0.021644 × 1123.309169 = 24.313239.
We already calculated the expected win from the bonus, before the first ball, is 0.308198. So, the overall variance of the bonus, before the first ball, is 24.313239 - 0.3081982 = 24.218253.
The next step is to calculate the covariance. "Why is there a correlation between the base win and the bonus win?", you might ask. It's because the last ball drawn must contribute to a win to trigger the bonus. Given that the last ball contributed towards a win, the average win goes up. As a reminder, Bayes' formula of condition probability says:
P(A given B) = P(A and B)/P(B).
Let's then redo our return table for the base game, given that the last ball was a hit:
Pick 8 Keno given Last Ball Hit
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| Total | 627,414,903 | 1.000000 | 6.757734 |
The bottom right cell shows that assuming the last ball was a hit, the average win is 6.757734.
Next, recall from your college statistics class that:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
In our case, let x = base game win and y=bonus win. Let's work on exp(xy) first.
Exp(xy) = prob(bonus won)*(average base game win given bonus won)*average(bonus win) + prob(bonus not won)*(average base game win given bonus not won)*average(bonus win given bonus not won). It's easy to say that average(bonus win given bonus not won) = 0, so we can rewrite as:
Exp(xy) = prob(bonus won)*(average base game win given bonus won)*average(bonus win) =
0.021644 × 6.757734 × 14.239212 = 2.082719.We already solved for E(x) and E(y), so the covariance is:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865.
Let's go back to the overall equation for the variance when covariance is involved:
Total variance = var(base game) + var(bonus) + 2*cov(base game and bonus) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191. The standard deviation is the square root of that, which is 6.869948.
So, there you go. That one took me hours, so I hope you're happy.
This question is asked and discussed in my forum at Wizard of Vegas.
I've heard the probability of a marriage ending in divorce, generally quoted as 50% in the United States, is calculated as the number of divorces to the number of marriages in the same period of time. Is that true? Do you think that is fair way to calculate the statistic? I question it because you're looking at divorces over a short time compared to marriages performed over a long time.
If the population and age distribution were stable, then if the divorce probability was truly 50%, then we would expect to see a ratio of one divorce to two marriages in any given period of time, given a large sample size.
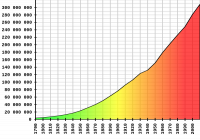
However, the population isn't stable. From this graph, it looks like the U.S. population is growing by 10.71% per decade. That comes to 1.02% per year. Let's just say 1% to keep it simple.
Map source: U.S. Census
According to fatherly.com, the average length of an unsuccessful marriage is 8 years.
If you were observing a 1 to 2 ratio of divorces to marriages in the present, what would be the average probability that any given marriage ends in divorce?
The divorces we're seeing now were from marriages 8 years ago, when the population was 92.35% what it is now. Simple math suggests the true probability of divorce is 54.14%.
Let's check that.
First, according to the CDC, there are 6.9 marriages to 1000 in population per year. This figure is not relevant to the question at hand, but I think helps see the numbers involved.
Suppose the population 8 years ago was 300,000,000. That would be 0.69% * 300 million = 2,070,000 marriages in that year.
If 54.14% of them end in divorce eight years later, then we would be seeing 2,070,000 * 54.14% = 1,120,698 divorces in the present.
1,120,698 / 2,070,000 = 50% observed ratio of divorces to marriages in the present.
Lest anyone say it, yes, I know that not all divorces end in exactly eight years. However, all things considered, I say that the bottom line won't be far from my 54.14% true divorce rate.
This question is raised and discussed in my forum at Wizard of Vegas.
Your office of 100 workers does a Secret Santa gift exchange. This where you write down everybody's name on individual pieces of paper, put them in a hat, and everybody draws a name at random to give a gift to.
The question is, how many closed loops will there be, on average? For example of a closed loop, Gordon gives to Don, who gives to Jon, who gives to Nathan, who gives to Gordon. Or drawing your own name.
Consider everybody choosing one at a time. As each person picks, there will be two types of situations:
- The name of the one picking has already been picked.
- The name of the one picking is still in the bin of names.
For any given picker, let's say there are n people left to pick.
If the name of the one picking has already been picked, there is a 1/n chance that the picker will choose close a loop involving his name. For example, let's say Amy is picking. Amy's name is already held by Bob, Bob's name is already held by Charlie, and Charlie's name is still in the bin. With n names still in the bin, there is a 1/n chance that Amy picks Charlie's name, closing a loop.
If the name of the one picking has not already been picked, there is a 1/n chance Amy picks her own name, closing a loop.
Either way, if the picker doesn't close a loop, she is joining part of another chain, which will eventually be closed by somebody else. Each chain should be counted once only, when it gets closed.
Thus the answer is 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
An estimate for any sufficiently large number of players, n, is ln(n).
The question is asked and discussed in my forum at Wizard of Vegas.
How much would an extra guaranteed wild be worth playing a video slot machine?
That depends on lots of things. The way I will interpret your question is what is the value of an extra wild above the average number the player would normally get. While the answer will vary significantly from game to game, a significant factor is the number of rows on the screen. If there are three rows, the extra wild will benefit 1/3 of the paylines. Likewise, if there are four rows, it will be less valuable, affecting 1/4 of the paylines.
To answer your question, I looked at the game Cleopatra, which I already deconstructed. The following table shows the increase in the expected value for a wild, compared to a random number of wilds.
Value of Extra Wild in Cleopatra
| Reel | 3 Rows | 4 Rows |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |