Ask The Wizard #293
I know there are some hands in video poker where two plays are equally good as the best play. For example, with a two pair in full pay deuces wild, the player should keep just one pair, and it doesn't matter which one. My question is whether there are any situations where there are three plays that are equally good as the correct play?
Yes! In joker poker, with a garbage hand, as a general rule it is best to keep one of the middle cards that has the best chances of forming a straight or flush on the draw. However, sometimes it is a close call, or even a tie, which is the best card to hold onto.
For example, in the 97.19% pay table for two pair joker poker and a Qh, 10d, 5d, 7c, and 2c on the draw, the best play is a tie between holding only the 10d, 5d, and 7c, with an expected value of 0.240703 for all three. This can be verified using my video poker hand analyzer.
Here are other such plays for the same joker poker pay table:
- QC 10S 5D 7H 2C
- QH 10D 5D 7H 2C
- KH 10D 5D 8C 3C
- KC 10S 5D 8H 3C
- KH 10D 5D 8H 3C
My thanks to Gary Koehler for his help with this question.
What is your opinion on how the new rules for the point after a touchdown will affect half point parlay cards?
For the benefit of other readers, one item in my bag of tricks is taking advantage of extra half points off of point spreads of 3 and 7 on half-point parlay cards. I've shown this to be a reliable, although very volatile, advantage play.
The new rule moves back the extra kick to the 15-yard line. This should lower the probability of success of the kick and induce more two-point conversion attempts. With more two-point conversion attempts, whether successful or not, there should not be as many games decided by three or seven points, thus lowering the value of getting the extra half point off these key numbers on half point parlay cards. Should we be worried? Let's see.
First, we should worry, but necessarily for this reason. Other rule changes have hampered the aggressiveness of the defense, leading to higher scoring games. The following graph shows the average number of points scored per game for each season from 1994 to 2014.
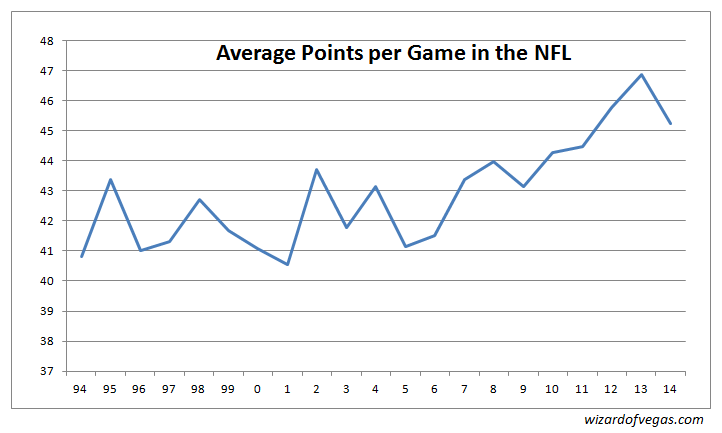
As the graph shows, the average points per game held close to 42 through 2006. However, starting in 2007, the average has been going up by about half a point per year. This leads to the question of whether this increase in the average score tends to flatten out the margin of victory distribution, especially for the magic numbers of 3 and 7. The next graph shows the probability of a three- and seven-point margin of victory by year.
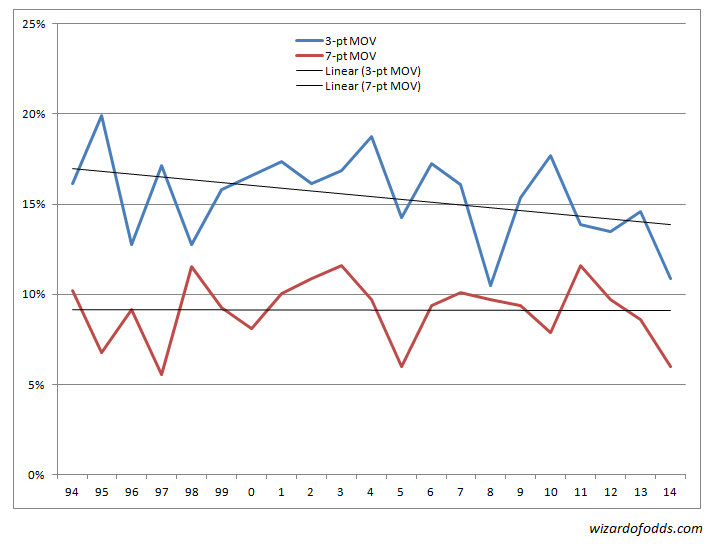
As you can see, the probability of a seven-point margin of victory is holding steady at 9.1%. However, the probability of a three-point margin of victory has been steadily declining, especially since 2004. This is bad because there are so many points spreads of three in the NFL.
Whatever the cause of the fewer three-point margins of victory, the value of the half point parlay cards is declining. Is it going to get even worse with the new extra point rule?
My answer is that it should hurt but not by much. Before the rule change, I calculate about 4.8% of touchdowns were followed by a two-point conversion attempt. As I write this, there have only been two weeks of games played since the rule change. In the first two weeks of the 2015 season, there were 167 touchdowns and 15 were followed by a two-point conversion attempt, for an attempt rate of 9.0%.
Mathematically speaking, I think going for the two-point conversion should be much more common, especially for variance-seeking weaker teams, and I don't understand why it isn't. That isn't what you asked, but I just had to get it off my chest.
Let's say, for the sake of example, I can go 54% against the spread consistently. For the sake of growing my bankroll as fast as possible, which would be fatter, flat betting of three-team parlays paying 6 to 1?
Good question. Your advantage laying 11 to 10 is 3.09% and on the parlay is 10.22%. That would seem to make a great case for the parlay.
However, remember that the optimal strategy for bankroll growth with any advantage play is to use the Kelly Criterion. According to Kelly, the optimal bet size is that which maximizes the expected log of the bankroll after the bet. For bets with just two possible outcomes, the optimal bet size is conveniently the advantage divided by what the bet pays on a "to one" basis.
Straight bets pay 10 to 11. That would make the optimal bet size 0.030909/(10/11) = 0.034000. At a player advantage of 3.09%, you can expect to win 0.001051 times your bankroll per game straight betting.
The optimal bet size on the parlay is 0.102248/6 = 0.017041. At a player advantage of 0.102248, you can expect to win 0.001742 times your bankroll per game straight betting .
However, straight betting is better because you get to bet three times. So multiply the expected gain per bet of flat betting by three to get 3 × 0.001051 = 0.003153. This is 81% more than the bankroll growth of parlay bets.
If your bankroll is so great that you bump against maximum bet limits, then you probably should make a parlay bet first, which tend to not move lines, and then get in your straight bets.
This question is raised and discussed in my forum at Wizard of Vegas.
As you know, the extra point must now be attempted from the 15-yard line in the NFL, which the two-point conversion attempt remains at the two-yard line. Do you think this changes the calculus in the decision? In other words, what is the correct play now?
It is a borderline call, which I think is what the NFL was after when they changed the rule. Things that should be considered in making the decision are:
- Probability of success by kicking.
- Probability of success by going for the two-point conversion.
- Overall chances of each team winning.
Late in the game, it is also critical to consider the key numbers. For example, if it is very late in the game and you just scored a touchdown to put your team ahead by three points, then you should kick. If you make it, you will be up by four points and force the other team to score a touchdown to win. If you go for two points, and miss, the other team can tie with only a field goal. So, I am going to limit my discussion to early in the game, when key numbers are not a big factor.
To answer your question, I wrote a simulation program. While it is rather crude, I think it is fairly accurate at reflecting the nature of the NFL in terms of field goals, touchdowns, and turnovers.
According to the article What Effect Will Moving Extra Points to the 15 Yard Line Have? by Kevin Rudy, the probability of making the extra point from the 15-yard line is 94.2%. I put into my program 94%, to keep the numbers nice and round.
There is more disagreement on the probability of making a two-point conversion. It would seem obvious this would also vary significantly according to the particular defense and offense. What I did was run simulations at two-point conversion success of 46% to 50%, in groups of 1%.
In each simulation, I had one team always kick and the opponent go for the conversion at each probability of success. I also ran simulations where both teams always kicked, to have something to compare the two-point conversion results against.
Table 1 below shows the results of two equally skilled teams. Team A always kicks after a touchdown. The table shows the probability team B winning and average additional points scored per game according to whether team B kicks or goes for the two-point conversion (2PC) and its probability of success.
Table 1 — Equal Teams
| Team B Strategy |
Team B Prob. Win |
Avg. Additional Points |
|---|---|---|
| Kick | 50.00% | 0.0001 |
| 2PC -- 46% | 49.76% | 0.0491 |
| 2PC -- 47% | 49.90% | 0.0000 |
| 2PC -- 48% | 50.05% | 0.0492 |
| 2PC -- 49% | 50.19% | 0.0980 |
| 2PC -- 50% | 50.33% | 0.1461 |
Note that with a probability of success of 47%, the expected additional points is 0.94 whether kicking or going for two points. However, the probability of winning is 0.1% less going for two points. I figure that is because if you miss, then the other team has the chance to tie with two field goals. It should be noted that this key number effect is quite small but does favor being conservative and kicking, all other things being equal. The bottom line is, with two equal teams, the probability of success with the two-point conversion should be at least 49% to go for it.
Table 2 below shows the results of two unequal teams, where team A is stronger. Team A always kicks after a touchdown. It shows the same statistics as table 1 above.
Table 2 — Team A Stronger
| Team B Strategy |
Team B Prob. Win |
Avg. Additional Points |
|---|---|---|
| Kick | 28.83% | -7.0039 |
| 2PC -- 46% | 29.01% | -7.0519 |
| 2PC -- 47% | 29.16% | -7.0039 |
| 2PC -- 48% | 29.30% | -6.9568 |
| 2PC -- 49% | 29.45% | -6.9083 |
| 2PC -- 50% | 29.60% | -6.8595 |
Table 2 shows the weaker team should go for the two-point conversion at all listed probabilities of success. Even at 45%, where the expected number of total points scored is less. Why is this, you might ask. This is because in any game, the weaker team should seek variance and the stronger team should abhor it.
Table 3 below shows the results of two unequal teams, where team B is stronger. Team A always kicks after a touchdown. It shows the same statistics as tables 1 and 2 above.Table 3 — Team B Stronger
| Team B Strategy |
Team B Prob. Win |
Avg. Additional Points |
|---|---|---|
| Kick | 71.17% | 7.0042 |
| 2PC -- 46% | 70.53% | 6.9349 |
| 2PC -- 47% | 70.67% | 7.0030 |
| 2PC -- 48% | 70.82% | 7.0725 |
| 2PC -- 49% | 70.97% | 7.1412 |
| 2PC -- 50% | 71.12% | 7.2109 |
Note that table 3 shows a probability of team B winning equal to 71.17% by kicking. It is less than that for all probabilities of success shown, even though the expected number of points is greater at a probability of success of 49% or 50%. The reason, again, is that weak teams should seek variance and strong ones should avoid it. The two-point conversion attempt adds volatility to the game, which is why weaker teams should be more inclined to attempt them, all other things being equal, than strong teams.




