Ask The Wizard #267
What would be the optimal strategy for dividing your money on the game show Million Dollar Money Drop, if you were not sure of the answer?
For the benefit of other readers, let me review the rules first.
- A team of players starts with $1,000,000.
- The team is given a multiple choice question.
- The team is to divide his money among the possible answers. Whatever money is put on the correct answer will move onto the next question.
- The team must completely rule out at least one possible answer by not putting any money on it.
- This process repeats for several rounds. The player is also given one chance to change his mind.
Obviously, if the team is sure of the answer then he should put all his money on the correct answer. If the team can narrow down the answer to two, but assigns each a 50% chance of being correct, then they should divide his money equally between the two choices.
Where it gets more difficult is if the team leans towards one answer but doesn’t completely rule out one or more of the others. Let’s look at an example. Suppose the team determines the probability of each correct answer as follows: A 10%, B 20%, C 30%, D 40%. How should they divide up his money?
I claim the answer is to follow the Kelly Criterion. Briefly, the team should maximize the log of his wealth with every question. To do this, you have to consider how much wealth you already have.
Let’s say your existing wealth, which you have accumulated independently of the show, is $100,000. It is your first question, so you have $1,000,000 of game show money to split up. First eliminate the option with the lowest probability, to conform with the show rules. Then you want to maximize 0.2×log(100,000+b*1,000,000) + 0.3×log(100,000+c*1,000,000) + 0.4×log(100,000+d*1,000,000), where lower-case a, b, and c refer to the portion placed on each answer.
This could be solved with calculus and solving a trinomial equation, trial and error, or my preference, the "goal seek" feature in Excel. Whatever you use, the right answer is to put 18.9% on B, 33.3% on C, and 47.8% on D.
Of course, nobody on the show is going to be able to do all this math in the time allowed, not to mention that you also have to move a lot of bundles of cash as well in that time. My more practical advice is to just divide up the money in proportion to your assessment of the probability of the answer’s being correct, assuming the least likely choice is not a possibility. In the example, that would cause a split of 22.2% on B, 33.3% on C, and 44.4% on D.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I heard of a casino where if the dealer busts then he assumes all players left standing won. The game is dealt face up, except double down cards are dealt face down. So if the double down card caused the player to bust, but the dealer also busted, then the player would win. The casino does this because it is paranoid about card counters, and doesn’t want players to see cards they think are irrelevant. What would be the correct basic strategy under this rule, and the house edge?
I’m going to assume six decks, dealer hits a soft 17, double after split, surrender, and re-splitting aces. If double for less is not allowed then I get a player edge of 4.9%. Here is that correct strategy. Obviously, this strategy may set off some red flags.
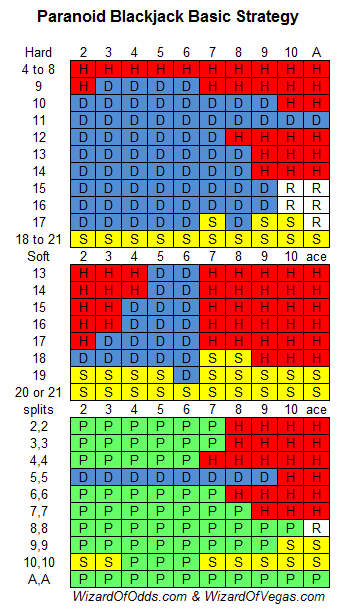
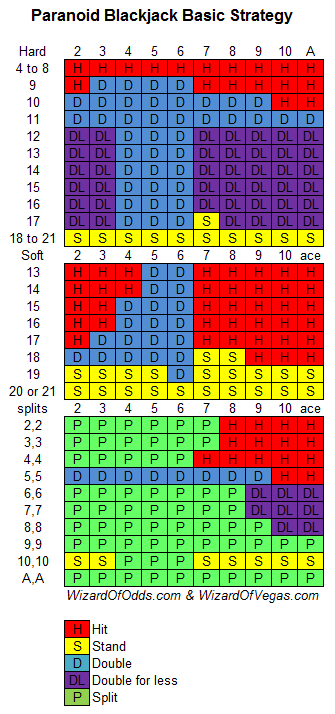
If double for less is allowed, then I get a maximum player edge of 9.4% with the following strategy. When doubling for less, bet as little extra as possible, preferably just one penny. My 9.4% figure assumes a tiny double down wager. In reality, most casinos require doubling with at least the table minimum.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
In Casino Vienna, there is a side bet in blackjack. The game uses six decks and the dealer stands on soft 17. It pays 5 to 2 if the dealer busts, regardless of the outcome on the original bet.
My blackjack appendix 2B was created for questions like this. It shows the probability the dealer will bust is 28.19% under those rules. That would make the house edge 1.33%.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
In your December 14, 2010 column you wrote that the AAAAAKK hand, which is specifically mentioned in the house way, may have never occurred in the history of the game. According to another dealer, a player got this hand at the Main Street Station in November 2010.
Interesting. As I wrote, I estimate that hand will occur about once every 23.7 years anywhere in Nevada. I’d say that was one of those times.




