Ask The Wizard #229
What kind of maximum bet would you recommend to a casino to limit the financial risk from high rollers? I am aware of the mathematical house advantage of blackjack, but that doesn’t change the fact a big player easily can do some serious damage to a casino if the limits are too high.
If I ran a casino, then I would apply the Kelly Criterion to setting maximum bets. What I would do is equalize m*v/h for all games, where m is the max bet, v is the variance, and h is the house edge. Let’s call this the risk quotient. For example, suppose I’m comfortable taking $150,000 on the Banker bet in baccarat, which is about what a big Strip casino will take. The house edge is 1.06%, and the variance is 0.932. The risk quotient is thus 150,000*0.932/0.0106 = 12,239,150.
Next, let’s solve for m to equalize the risk quotient in blackjack. With liberal Strip rules, the house edge is 0.29%. Let’s say the player can bet up to three spots. The standard deviation per hand, given three bet spots, is 1.51957, so the variance is 1.519572 = 2.3091. Solving for m...
m×2.3091/0.0029 = 12,239,150
m = $15,371.
As a practical matter, few players play perfect basic strategy, so I might bump that up to $20,000. That is about what the big Strip casinos will take in blackjack, so I think there is proportionality there. It is the novelty games where I think they should be taking bigger bets.
I was involved in a hand of online poker and would like to know the odds of this happening, please:
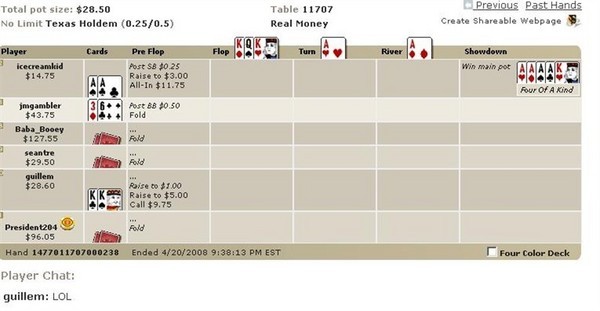
Normally I'm sick of bad beat questions, but this one was too painful to ignore. Before the first card is dealt, the probability of four kings being beaten by four aces, in a two-player game, with both players having pocket pairs, is 2*combin(4,2)*combin(4,2)*44/(combin(52,2)*combin(50,2)*combin(48,5)) = 2*6*6*44/(1326*1225*1712304) = 1 in 877,961,175. This was a six-player game, so there are combin(6,2) = 15 different player pairs. In a six-player game, the probability is 15 times higher, or 1 in 58,530,745. After the indicated hole cards are dealt, and before the flop, the probability is 1 in 38,916 that the hand will finish as it did.
Your pai gow (tiles) strategies are optimized for the Foxwoods House Way, which was dated February 1997. In some of your strategies, there appears to be a player edge, or close to even odds. Do you know if any of the casinos in Vegas or elsewhere have read your website, and adjusted their house ways accordingly? Do you have any more updated information about house ways at different casinos? Also, on your odds table for pai gow, you have an "optimal" strategy, but it’s not clear to me where the rules for that strategy are. What is the "optimal" strategy? I’m really enjoying the game, and looking for ways to grind it out, have fun and get comps without losing too much money.
Caesars Palace here in Vegas changed their house way in the last few years. Previously, they never split up the gee joon pair, and now they do. A dealer at the Mandalay Bay recently commented to me about a rule change to play 0-7 over 3-4. About the reason behind the changes, I have no idea. I would be proud if I had something to do with it.
I recently added a house way for the Casino Canberra. In the future I may also add house ways for the Claridge in Atlantic City and Treasure Island in Las Vegas. It is tedious and time consuming to put them into HTML, which is why I have not done those yet.
My assistant JB is working on an optimal strategy against the Foxwoods house way. It should be up on the site shortly.
The game of one-card poker has a three-card deck, an ace, deuce, and trey. The ace is lowest and the trey is highest. Each of two players antes $1 into the pot. Then, each player gets one card. The order of betting is predetermined, with player 1 to act first. Player 1 may either bet $1 or check. If player 1 bets, player 2 may either call or fold. If player 1 checks, then player 2 may either bet $1 or check. If player 1 checks, and player 2 bets, then player 1 may either call or fold. If both players check, or both bet, then the higher card wins the pot. Assuming both players are perfect logicians, what is the optimal strategy for each player?
I hope you’re happy; I spent all day on this. The answer and solution can be found on my other site mathproblems.info, problem 203, or the academic paper Game Theory and Poker by Jason Swanson.




