Ask The Wizard #227
Three years ago, in an Ask The Wizard column, you wrote: "You are right that 500 is too few to make a good case for or against influencing the dice, but 500 throws is better than zero." Can you describe what you would require from an alleged dice influencer, in an experiment, in order for you to feel confident enough to start betting significant amounts of money on him? I ask because one billion rounds is a good benchmark for "reliable" results in some blackjack sims. With the most efficient (i.e. requiring least amount of rolls) experimental design you can think of, how many rolls would need to be made by the shooter to be confident he is influencing the outcomes? I know the answer will depend on the skill of the shooter, but you get my drift. If you need a million rolls even under the best case scenario, it’s not going to be a worthwhile endeavor.
There is no definitive point at which confidence is earned. It is a matter of degree. First, I would ask what is being tested for, and what the shooter estimates will happen. With any test there are two possible errors. A skilled shooter might fail, because of bad luck, or a random shooter might pass because of good luck. Of the two, I would prefer to avoid a false positive. I think a reasonable test would set the probability of a false negative at about 5%, and a false positive at about 1%.
For example, suppose the claimant says he can average one total of seven every seven throws of the dice. A random shooter would throw one seven every six throws, on average. By trial and error I find that a test meeting both these criteria would be to throw the dice 3,600 times, and require 547 or fewer sevens to pass, or one seven per 6.58 rolls.
A one in seven shooter should average 514.3 sevens, with a standard deviation of 21.00. Using the Gaussian approximation, the probability of such a skilled shooter throwing 548 or more sevens (a false negative) is 5.7%. A random shooter should average 600 sevens, with a standard deviation of 22.36. The probability of a random shooter passing the test (a false positive) is 0.94%. The graph below shows the possibe results for skilled and random shooters. If the results are to the left of the green line, then I would consider the shooter to have passed the test, and I would bet on him.
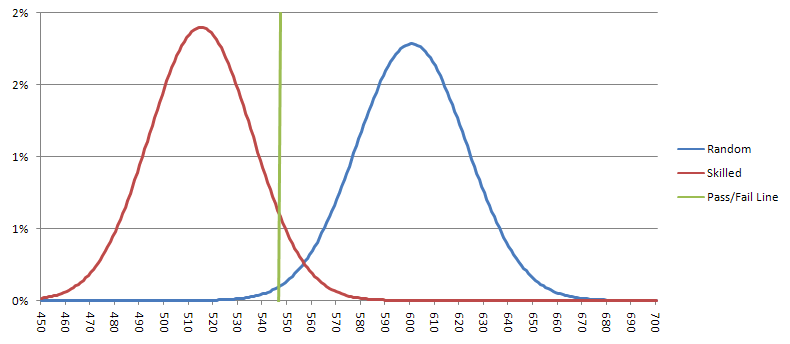
The practical dilemma is if we assume two throws per minute, it would take 30 hours to conduct the test. Perhaps I could be more liberal about the significance level, to cut down the time requirement, but the results would not be as convincing. I do think the time has come for a bigger test than the 500-roll Wong experiment.
If the Lucky Lady side bet is only played when the true count is, say, 10 or above, will one beat the house edge? If so, what is the minimum true count at which one can beat the house edge with this side bet?
I have not studied the effect of card counting of that bet for myself. However, Arnold Snyder has, and his results can be found in his Big Book of Blackjack. There he says you should make the bet in a six-deck game if it is the last two decks, and the count is +10 or greater, using the Red Sevens count. In a double-deck game he says to bet in the last deck, and a count of +6 or greater.
What gain is there for a player when the house allows late surrender on a 6-deck shoe, when the house hits soft 17, and when the house stands on soft 17? What about an 8-deck shoe?
Answers to questions like that can be found using my house-edge calculator by changing a rule and noting the effect on the house edge. Normally I would make you do it, but I’m in a patient mood today, so here you go:
6 decks, dealer stands on soft 17: 0.0726%
8 decks, dealer stands on soft 17: 0.0758%
6 decks, dealer hits on soft 17: 0.0882%
8 decks, dealer hits on soft 17: 0.0916%
I was wondering if there is a way to calculate on average how many trials it would take to lose ten units from any given point, betting on Player in baccarat.
The house edge on the Player bet is 1.2351%, assuming eight decks. The expected number of hands it takes to have a loss of ten units is 10/0.012351 = 809.66.
I was recently in a home poker game (Omaha deuces wild) with some family members. There were five players, and went down to two. I was one of the two. The other player had been winning all night. I finally had a good hand. I looked over and in a mocking way called "four sevens." She said that she had four aces, and proceeded to rake the chips. I then corrected myself, and told that I had a straight flush. She then told me that I already called four sevens. I showed my hand and she still insisted that I already called four sevens, and my hand was not good any more. So the question is who won the hand? Clearly the straight flush beats a four of a kind. But did I muck my hand by saying what I said? The money is still on the table.
Ultimately, the cards speak. You should have won that hand.




