Probabilities in Five Card Stud Poker
Hi, this is Mike, and the purpose of this video will be to show you how to calculate the probabilities in five-card stud poker. In other words, what is the probability of forming any given poker hand given five random cards out of 52. Before I answer the question on the number of combinations of each poker hand, let me ask you a simpler question, and if you know how to get the answer, you can skip ahead.
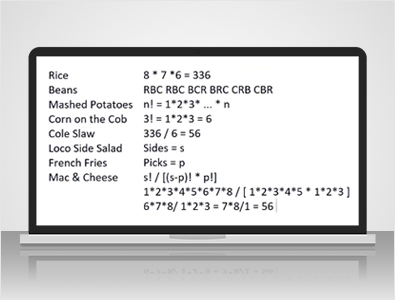
In El Pollo Loco:
They have eight so-called classic sides which I listed on the left. They also have some deluxe sides, but I won't muddy the waters with that. If you order the 12-piece meal, you can pick any three of these eight sides. Let's pretend that you must pick three different things.
The question is...
...how many ways can you order three different sides out of eight? In other words, let's say that you go there every day, and every day you order three different sides. How many days could you go without repeating the same three sides?
If the order mattered that you ordered them in, then the answer would be 8 x 7 x 6 because there are eight ways you could pick the first one, seven ways you could pick the second one, and six ways you could pick the third one, but the cashier doesn't care. The order that you ordered them.
If you say -
"I want rice, beans, and corn," you're going to get the same thing whether you say, "rice, beans, and corn," or "corn, beans, and rice." How many different ways can you order three different sides? Well, let's say that you do like rice, beans, and corn. You could order them in that order, you could order rice, corn, beans, you could order beans, corn, rice. You could order beans, rice, corn or corn, rice, beans or corns, beans, rice, so six possible ways.
How did I know it was six without just writing them down?
Well, there's a very simple formula. If there are N items there, the number of ways you can order them is 1 x 2 x 3 times all the way up to N.
In this case, the question was, how many ways can you order three things? Well, that's 3! which is 1 x 2 x 3, which equals 6. Of the 336 ways you can order the three items out of eight with regard to order, you divide by six because there are six ways to order each combination, and that leaves you with 56.
What is the general formula, you might ask?
If there are, let's say that the number of sides equals S, and the number of picks you're allowed is P, the general formula for the number of ways you can pick P things out of S is s! / s - p! x p!. Let me show that this works with the example question.
In this case:
s = 8, so 8! is 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8, and then the denominator we have s - p, or 8 - 3, which is 5 or 5!. So, 1 x 2 x 3 x 4 x 5, as well as p! or 3!, which is 1 x 2 x 3. You can see 1 x 2 x 3 x 4 x 5, which equals 120, and both the numerator and denominator, so let's cancel that out, leaving us with 6 x 7 x 8 / 1 x 2 x 3. Well, 2 x 3 = 6, and there's a six appearing in both the numerator and denominator, so let's divide that out.
We're left with just...
...7 x 8 / 1, which is 56. For purposes of this video, let me introduce a function. We'll call the function C of x and y as the number of ways to choose y items out of x, or x choose y, as we would say, mathematically, and we'll define that as x! / x - y! times y!.

In the case of the El Pollo Loco example, if the question was:
"How many ways can you choose three slides out of eight?"
We would express it like that, which would be equal to-- the switch equals 56. I think that we're finally ready to start talking about poker. What are the number of ways you can pick five cards out of 52? Well, that would be 52 choose 5, which is 52! / 47!, 47 because 52 - 5 x 5!, and that equals 2,598,960. Let's start with a royal flush.
Well, that's pretty easy. There's four suits for the royal flush: hearts, spades, clubs, and diamonds. The ranks must be ten, Jack, Queen, King, Ace. Yes, there's just four ways. A royal and hearts, diamonds, clubs, or spades.
How about a straight flush?
Well, again, we still have the four suits, but the span of the straight flush can start as low as an Ace, meaning the Ace, two, three, four, five, otherwise known as the wheel straight flush, all the way up to nine, ten, Jack, Queen, King. If it were ten, Jack, Queen, King, Ace, then it would be a royal flush. The lowest card can be anywhere from an Ace to a nine.
In this case...
...the Ace counts as like a one. There's nine possible spans for the straight flush, so 4 suits x 9 spans = 36. With the four of a kind, there are 13 possible ranks for the four of a kind, for example, Queens, and then there are 48 cards left in the deck for the singleton after you take out the four cards for the four of a kind. That equals 624.
For the full house
There are 13 possible ranks for the three of a kind, and 12 ranks left for the pair. For the three of a kind, there are four choose, three ways to pick three suits out of four times four choose, two ways to pick two suits out of four, for the pair. That equals 13 x 12 x 4 x 6 which equals 3,744. For the flush, well, we've got four suits for the flush.
How many ways are there to pick five ranks out of the 13 in the given suit?
Well, that would be 13 choose 5, but 10 of those ways would result in a straight flush or a royal flush. For example, 5, 6, 7, 8, 9 would result in a straight flush, so we have to pick out those 10 sets of ranks that are consecutive. That leaves us with 13 choose 5 is 1,287, subtract out the 10 and multiply by 4, and we get 5,108.
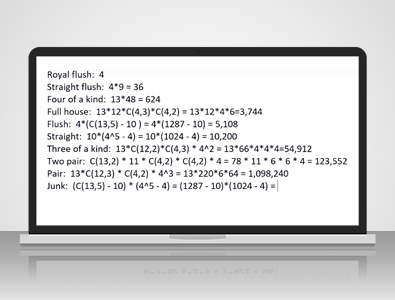
How about a straight?
Well, as we just saw with the flush, there are 10 possible spans for the straight starting with Ace, two, three, four, five going all the way up to 10, Jack, Queen, King, Ace. For each card, for each rank in that straight, there are four possible suits. 4 x 4 x 4 x 4 x 4= 4^5, the number of ways to choose a different suit for each of the five cards. If we choose the same suit all five times, then we will also be left with a straight flush or royal flush. We need to subtract those out. 4^5= 1,024 - 4 =10,200 ways to make a straight.
How about a three of a kind?
Well, there are 13 ways you can choose the rank of the three of a kind, and then you have to choose two ranks out of the 12 remaining for the two singletons. Once you do that, you have to pick four out of three suits for the three of a kind, then one suit out of four for each of the two singletons.
We are left with 13 ways to choose the rank of the three of a kind. There are 66 ways to choose two ranks out of the 12 left for the two singletons times four ways to choose the three suits out of four for the three of a kind, and also four ways to choose one suit for the two singletons. The answer is 54,912.
How about a two pair?
Well, there are 13 choose two ways to pick two ranks out of 13 for your two pair, then you'll have one rank left for the singleton. For each of the pairs, there are four choose two ways to pick two suits our of four for your pair. There are four suits for your singleton. 13 choose two equals 78 times six times six times four equals-- I forgot my 11 ranks for the singleton. 78 x 11 x 6 x 6 x 4= 123,552.
For the pair
There are 13 ways you can choose the rank of the pair, then you have to pick three ranks out of the twelve left for the three singletons. For your pair, there are four choose two ways to pick two suits out of four, then for each of the three singletons, there's four possible suits to choose from. 4 x 4 x 4 is the number of ways you can choose three suits for your three singletons, that equals 13 x 12-- 12 choose three equals 220 x 6 x 4^3= 64= 1,098,240.
Finally
Let's calculate the probability of having Ace higher left or less which I'll just call junk. In order to have junk, you must have five different ranks out of the 13. There's 13 choose five ways to pick five ranks out of ten, but as we saw with the flushes, we have to set track out the tenth spans that form a straight. Once you've picked your five non-consecutive ranks, there's four possible suits for each of the ranks.
You take four to the fifth power...
...and as we saw with the straights, we have to subtract out four for the number of ways to pick the same suit each time which would result in a flush. 13 choose five equals 1,287 minus 10 for the straights times four to the fifth power equals 1,024 minus four equals 1,302,540.
Next
Let's put that all in a spreadsheet. Let me quickly show you how to do all that in Excel. We already saw there's just four ways to get a royal flush, one for each suit, 36 straight flushes, four suits times nine possible spans. For your four of a kind, there's 13 ranks to choose from four, the four of a kind and 48 cards left over for the singleton. For the full house, there's 13 ranks for the three of a kind, 12 for the pair.
Four choose three ways to choose the suits of the three of a kind. Four choose two ways to choose two suits out of four for the pair. The way you express that formula in Excel is with this common formula combining big number comma small number, just like I wrote it out there. That gives us the 3,744 we got earlier.
For the flush
There's four suits to choose from, 13 choose five ways to pick, five ranks out of 13 in that suit minus 10 spans that would result in a straight flush or a royal flush because they're consecutive. That leaves us with 5,108 flushes. For the straights, there are 10 possible spans, four suits for each card in the span, but subtract out four for the four suits which would leave you with a straight flush or royal flush and we get the 10,200.

For the three of a kinds
There's 13 ranks, for the three of a kind, 12 choose two ranks for the two singletons. Four choose three ways to pick three suits out of four and four times four ways to choose the two suits for the two singletons. 554,912, three of a kinds. For the two pairs, there are 13 choose two ways to choose two ranks out of 13 for the two pairs. 11 left for the singleton, four choose two ways to pick two suits out of four for the two pairs and four suits for the singleton.
For the pair, we have 13 ranks for the pair, 12 choose three ways to pick three ranks out of 12 for three Singletons. Four choose two ways to pick two suits out of four for the pair and four to the third power for the ways to pick three suits for the three Singletons.
Finally, for the junk
There are 13 choose five ways to pick five ranks out of 13 minus the 10 consecutive ways that would give you a straight and four ways to choose each of the suits. Four to the 5th power minus four for the ways it would give you a flush. As you can see the sum of all these is 2,598,960 which we also got at the beginning of this video. Okay, let's go to a practical application of all this.
One of the hundreds of casino games that I cover at my website Wizard of Odds here is called: Let it ride.
Let's pull up that page and this is a poker game based upon a five-card poker hand, there's no drawing it's all based on just five random cards out of 52. I won't get into the whole rules of the game but there is a side bet that pays based on just the poker value of your five cards.
You can see...
...that I list nine of these possible pay tables here but table four here is a pretty common one. I already transcribed it into this table here, the bet cost $1. If you get a royal flush you win $20,000, a straight flush wins 20,000, a four of a kind wins 400. These pay, by the way, are on a 4-1 basis meaning that you don't keep your original bet if you win.
Here's all the combinations which I already worked out the probabilities and this return column here is the product of the win times the probability.
For example, there is:
As we know from before there is about a four and two point six million chance of getting a royal flush. If we multiply that probability times 20000, it results in expected return of 3.08 cents. That's how much the player if he bets a dollar he can expect to get back in the form of royal flush winnings. He can expect to get back to 2.77 cents for his straight flushes and so on.
If you do all the math at the bottom line is that for the players, $1 bet he can expect to get back 74.4667 cents. In other words, for that dollar, the player can expect to get back about 74.47% and the casino will keep 25.53%.
The way I would express that...
...is the house advantage is 25.53% so just let that sink in for a minute. The casino is keeping more than 25% of that bet which just goes to show what I have been saying for over 20 years that side bets are all sucker bets. If you learn just one thing from this video I hope it's that. This is run long enough as it is, my apologies for the length and I hope this was informative and that you learned something.
Thank you for watching.




