On this page
Three Card 2nd Chance Poker
Introduction
Three Card 2nd Chance is a poker-based game, invented and patented by me (patent number 7,735,830). The "Best Hand Bonus" side bet was the idea of WagerWorks. Three Card 2nd Chance follows the same structure as a five-card version, Five-Card Mulligan Poker, which has been available at Odds On Internet casinos since May 2007. The thrust of the game is that if the player doesn't like his first hand, he may exchange it for a second hand by merely increasing his bet. The dealer also has the ability to replace his hand in certain circumstances. Then, the higher hand wins, and all wins pay at least even money. WagerWorks has an exclusive license to be the sole provider of Three Card 2nd Chance for Internet-based casinos. I would be happy to hear from "brick and mortar" casinos interested in offering the game.
Rules
- A single 52-card deck is used. All hands are scored according to conventional poker rules, except the hand order is altered for 3-card hands.
- Play starts with the player making an Ante bet. The player may optionally make a "Best Hand Bonus" bet as well. The most the player may bet on the Best Hand Bonus is two times the Ante bet.
- The dealer shall give the player three cards and herself three cards. Player cards will be face up and dealer cards face down.
- The player has the choice to either stand or to trade in his hand for a new three-card hand.
- If the player chooses to trade, then he should discard his cards and make a Raise wager equal to the Ante wager.
- The dealer will then turn over his cards.
- If the dealer has a king high or higher, he will stand.
- If the dealer has a queen high or less, he will discard his hand for three new cards.
- The dealer will then compare her own hand to the player's hand, and the higher hand wins. If the dealer has the higher hand, then the player will lose his Ante wager as well as any Raise wager. If the player has the higher hand, then both Ante wager and Raise wager will be paid according to the Ante and Raise pay table below. This table also reflects the hand ranking order. A tie will result in a push.
Ante and Raise Pay Table
Hand Pays Straight flush 6 to 1 Three of a kind 4 to 1 Straight 3 to 2 All other 1 to 1 - The Best Hand Bonus wager shall pay according to the higher of the player's and dealer's final hands, as follows.
Best Hand Bonus Pay Table
Hand Pays Three aces 35 to 1 Straight flush 15 to 1 Three of a kind 12 to 1 Straight 3 to 1 Flush 2 to 1 All others Loss 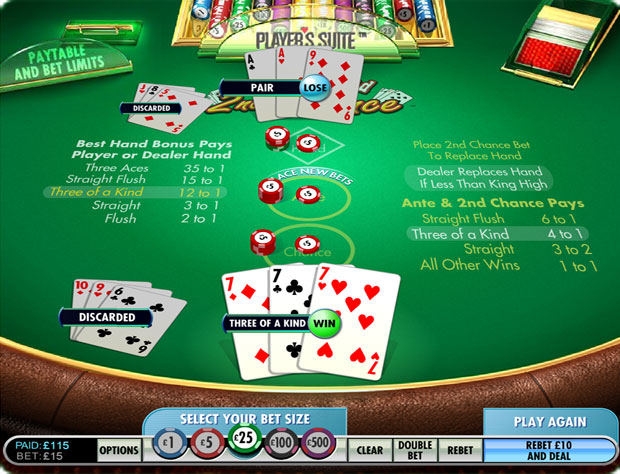
Screenshot courtesy of WagerWorks
Strategy
If the player makes the ante wager only, then the optimal strategy is to switch with K87 or less, and stand on K92 or more.
If the player makes the maximum Best Hand Bonus bet, then the optimal strategy is to switch with AQJ or less, and stand with AK2 or more.
Of the two bet mixes, the one that results in the lower overall house edge is to make the maximum Best Hand Bonus bet.
Ante Only Analysis
The next table shows the possible outcomes if the player bets the Ante only, switching with K87 or less.
Ante Only Return Table — Switch with K87 or Less
| Event | Bet | Pays | Probability | Return |
|---|---|---|---|---|
| Player wins with straight flush | 2 | 12 | 0.001041 | 0.012497 |
| Player wins with three of a kind | 2 | 8 | 0.001125 | 0.009002 |
| Player wins with straight flush | 1 | 6 | 0.002176 | 0.013055 |
| Player wins with three of a kind | 1 | 4 | 0.002349 | 0.009395 |
| Player wins with straight | 2 | 3 | 0.015199 | 0.045598 |
| Player wins with straight | 1 | 1.5 | 0.031641 | 0.047461 |
| Player wins with flush | 2 | 2 | 0.021846 | 0.043693 |
| Player wins with pair | 2 | 2 | 0.061861 | 0.123722 |
| Player wins with nothing | 2 | 2 | 0.080141 | 0.160282 |
| Player wins with flush | 1 | 1 | 0.045172 | 0.045172 |
| Player wins with pair | 1 | 1 | 0.127912 | 0.127912 |
| Player wins with nothing | 1 | 1 | 0.117501 | 0.117501 |
| Player ties | 2 | 0 | 0.000482 | 0 |
| Player ties | 1 | 0 | 0.000637 | 0 |
| Player loses | 1 | -1 | 0.189183 | -0.189183 |
| Player loses | 2 | -2 | 0.301734 | -0.603468 |
| Total | 1 | -0.03736 |
The lower right cell shows a house edge of 3.736%. The player will raise 48.34% of the time, for an average final wager of 1.4834 units. That makes theElement of Risk 3.376%/1.4834 = 2.518%.
2 to 1 Ratio of Side Bet to Ante Analysis
When the player makes the Best Hand Bonus bet, he should be more aggressive about switching. The following table shows the outcome of the Ante wager when the player switches on AQJ or less, the optimal strategy when making the maximum Best Hand Bonus side bet.
Ante Only Return Table — Switch with AQJ or Less
| Event | Bet | Pays | Probability | Return |
|---|---|---|---|---|
| Player wins with straight flush | 2 | 12 | 0.001553 | 0.018641 |
| Player wins with three of a kind | 2 | 8 | 0.001669 | 0.013354 |
| Player wins with straight flush | 1 | 6 | 0.002174 | 0.013046 |
| Player wins with three of a kind | 1 | 4 | 0.002345 | 0.009379 |
| Player wins with straight | 2 | 3 | 0.022650 | 0.067950 |
| Player wins with flush | 2 | 2 | 0.032376 | 0.064751 |
| Player wins with straight | 1 | 1.5 | 0.031611 | 0.047416 |
| Player wins with pair | 2 | 2 | 0.091599 | 0.183197 |
| Player wins with nothing | 2 | 2 | 0.118533 | 0.237066 |
| Player wins with flush | 1 | 1 | 0.045192 | 0.045192 |
| Player wins with pair | 1 | 1 | 0.127938 | 0.127938 |
| Player wins with nothing | 1 | 1 | 0.016185 | 0.016185 |
| Player ties | 1 | 0 | 0.000170 | 0 |
| Player ties | 2 | 0 | 0.000704 | 0 |
| Player loses | 1 | -1 | 0.057368 | -0.057368 |
| Player loses | 2 | -2 | 0.447933 | -0.895867 |
| Total | 1 | -0.109119 |
The next table shows the possible outcomes of the Best Hand Bonus bet, when the player switches with AQJ or less.
Best Hand Bonus Return Table — Switch with AQJ or Less
| Event | Pays | Probability | Return |
|---|---|---|---|
| Three aces | 35 | 0.000569 | 0.019902 |
| Straight flush | 15 | 0.006811 | 0.102171 |
| Three 2-K | 12 | 0.006783 | 0.081396 |
| Straight | 3 | 0.099023 | 0.297068 |
| Flush | 2 | 0.140714 | 0.281428 |
| Loser | -1 | 0.746100 | -0.746100 |
| Total | 1 | 0.035865 |
The Ante wager table shows a player return of -10.912%. The Best Hand Bonus table shows a player return of 3.587%. Taking a weighted average, the overall player return is (1/3)×-0.109119 + (2/3)×0.035865 = -0.012463. So, the combined house edge is 1.246%. The player will raise 71.7% of the time, for an Element of Risk of 1.006%.
Methodology
This analysis was done by random simulation. With the possibility of both player and dealer switching cards, the number of possible combinations is combin(52,3) × combin(49,3) × combin(46,3) × combin(43,3) = 76,277,828,779,152,000, which would take years to loop through.



