On this page

Plinko

On this page

Introduction

Plinko is the general term for a game involving a ball or disk that falls randomly down a grid of pegs, known as a Galton Board, to land in a random spot at the bottom. Such boards are also a good way to illustrate a Gaussian curve at science museums. In the case of the casino game, the concept is the same, but where the ball lands will determine how much the player wins/loses.

This page presents three variants of Plinko I have seen, by CryptoGames Casino, BGAMING (software), and BetFury Casino.

CryptoGames Rules

Following are the rules for how the game is played at CryptoGames.

  1. The player chooses a bet and a pay table (green, red, blue, or yellow).
  2. Bets are made in "credits." A credit costs 0.000001 BTC (Bitcoin) and the minimum bet is 10 credits.
  3. A ball is dropped from above a triangular field of pegs, with 16 rows and 17 possible places to land at the bottom.
  4. At each row, the ball will hit a peg and may either go left or right, each with a 50% chance.
  5. When the ball reaches one of the 17 possible resting spots at the bottom, the player will be paid according to amount bet, where the ball landed, and pay table chosen.

Per the concept of "provably fair gaming" common to Cryto-casinos, the final outcome is determined in advance. With 16 rows of pegs, there are 2^16 = 65,536 possible paths the ball can take. The final outcome is based on a random number from 0 to 65,535, which gets mapped according to one of the positions at the bottom of the grid. I have checked and the mapping is done correctly, according to the natural odds of a fair Plinko board.

The following table shows the number of combinations for each outcome, the range associated with it, and what each of the four pay tables pay for that position. All pays are on a "for one" basis.

Crypto Games Casino
Players rated Crypto Games Casino 2.9 out of 5 Stars

Sign Up Bonus

100% up to
₮10000

New customers only. T&C apply. 18+.This offer is not available for players residing in Ontario. New Customer Offer. T&C’s Apply. 19+. Max Bet: $15. From day of activation bonus will be valid for 7 days. Selected games only: See the website for a list of online slots.
US-OH Friendly
Visit Casino

Plinko Pay Table

Position Combinations Range Green
Pays		 Red
Pays		 Blue
Pays		 Yellow
Pays
0 1 0 to 0 10 20 50 650
1 16 1 to 16 8 7 8 30
2 120 17 to 136 6 5 3 7
3 560 137 to 696 3 3 2 3
4 1,820 697 to 2516 2 2 1.4 1.5
5 4,368 2517 to 6884 1.3 1.1 1.2 1.2
6 8,008 6885 to 14892 1 1 1.1 1
7 11,440 14893 to 26332 0.8 0.6 1 0.7
8 12,870 26333 to 39202 0.5 1 0.4 0.7
9 11,440 39203 to 50642 0.8 0.6 1 0.7
10 8,008 50643 to 58650 1 1 1.1 1
11 4,368 58651 to 63018 1.3 1.1 1.2 1.2
12 1,820 63019 to 64838 2 2 1.4 1.5
13 560 64839 to 65398 3 3 2 3
14 120 65399 to 65518 6 5 3 7
15 16 65519 to 65534 8 7 8 30
16 1 65535 to 65535 10 20 50 650

Analysis

The following table shows my analysis of the Green pay table. The lower right cell shows an expected return of 98.37%.

Green Pay Table Analysis

Position Combinations Pays Probability Return
0 1 10 0.000015 0.000153
1 16 8 0.000244 0.001953
2 120 6 0.001831 0.010986
3 560 3 0.008545 0.025635
4 1,820 2 0.027771 0.055542
5 4,368 1.3 0.066650 0.086646
6 8,008 1 0.122192 0.122192
7 11,440 0.8 0.174561 0.139648
8 12,870 0.5 0.196381 0.098190
9 11,440 0.8 0.174561 0.139648
10 8,008 1 0.122192 0.122192
11 4,368 1.3 0.066650 0.086646
12 1,820 2 0.027771 0.055542
13 560 3 0.008545 0.025635
14 120 6 0.001831 0.010986
15 16 8 0.000244 0.001953
16 1 10 0.000015 0.000153
Total 65,536   1.000000 0.983701

The following table shows my analysis of the Red pay table. The lower right cell shows an expected return of 98.16%.

Red Pay Table Analysis

Position Combinations Pays Probability Return
0 1 20 0.000015 0.000305
1 16 7 0.000244 0.001709
2 120 5 0.001831 0.009155
3 560 3 0.008545 0.025635
4 1,820 2 0.027771 0.055542
5 4,368 1.1 0.066650 0.073315
6 8,008 1 0.122192 0.122192
7 11,440 0.6 0.174561 0.104736
8 12,870 1 0.196381 0.196381
9 11,440 0.6 0.174561 0.104736
10 8,008 1 0.122192 0.122192
11 4,368 1.1 0.066650 0.073315
12 1,820 2 0.027771 0.055542
13 560 3 0.008545 0.025635
14 120 5 0.001831 0.009155
15 16 7 0.000244 0.001709
16 1 20 0.000015 0.000305
Total 65,536   1.000000 0.981561

The following table shows my analysis of the Blue pay table. The lower right cell shows an expected

Blue Pay Table Analysis

Position Combinations Pays Probability Return
0 1 50 0.000015 0.000763
1 16 8 0.000244 0.001953
2 120 3 0.001831 0.005493
3 560 2 0.008545 0.017090
4 1,820 1.4 0.027771 0.038879
5 4,368 1.2 0.066650 0.079980
6 8,008 1.1 0.122192 0.134412
7 11,440 1 0.174561 0.174561
8 12,870 0.4 0.196381 0.078552
9 11,440 1 0.174561 0.174561
10 8,008 1.1 0.122192 0.134412
11 4,368 1.2 0.066650 0.079980
12 1,820 1.4 0.027771 0.038879
13 560 2 0.008545 0.017090
14 120 3 0.001831 0.005493
15 16 8 0.000244 0.001953
16 1 50 0.000015 0.000763
Total 65,536   1.000000 0.984814

The following table shows my analysis of the Yellow pay table. The lower right cell shows an expected return of 98.09%.

Yellow Pay Table Analysis

Position Combinations Pays Probability Return
0 1 650 0.000015 0.009918
1 16 30 0.000244 0.007324
2 120 7 0.001831 0.012817
3 560 3 0.008545 0.025635
4 1,820 1.5 0.027771 0.041656
5 4,368 1.2 0.066650 0.079980
6 8,008 1 0.122192 0.122192
7 11,440 0.7 0.174561 0.122192
8 12,870 0.7 0.196381 0.137466
9 11,440 0.7 0.174561 0.122192
10 8,008 1 0.122192 0.122192
11 4,368 1.2 0.066650 0.079980
12 1,820 1.5 0.027771 0.041656
13 560 3 0.008545 0.025635
14 120 7 0.001831 0.012817
15 16 30 0.000244 0.007324
16 1 650 0.000015 0.009918
Total 65,536   1.000000 0.980899

Summary

The following table shows the return and standard deviation for each pay table. The greatest return is for the Blue pay table, at 98.48%.

Summary

Pay Table Return Standard
Deviation
Green 98.37% 0.562711
Red 98.16% 0.517632
Blue 98.48% 0.464829
Yellow 98.09% 3.678698

Probably Fair

The way "provably fair" mechanism works, at least at Crypto.Games, is as follows:

  1. Enter a string consisting of the casino hash followed by the player hash into a SHA512 hash generator, like this one.
  2. Convert the first four characters in the hash from step 1 into a hexi-decimal to base-10 converter, like this one.
  3. The result of step 2 will be an integer from 0 to 65535 (164-1). This result is mapped to an outcome according to the ranges in the first table of this page.

The way this is "provably fair," is the casino will provide the hash of its own seed before you bet, ensuring the casino's contribution to the outcome was predestined, assuming the casino seed provided after the bet matches that hash.

If this sounds Greek to you, I go through the concepts and terminology of using cryptography for fair gaming in my page on Dice (Encrypted Version) more slowly.

If you want to simplify the process above, I welcome you to use this program I saved at PHP Sandbox. Just enter the Server Seed on line 4, the Client Seed on line 5, and click "execute code." The game outcome will be in the Results box below the code.

You may also see my code by clicking the button below.

// Plinko game conversion for Crypto.Games

$server_seed = "k34pQFblHvQAJ33zZZHCQtlFlhHb4KTtw2qhOahC";
$client_seed = "6VoqO9MXdSp5xSmiq2L6xcvn2XVvFWVLkC0TtLwc";
$combined_seed = $server_seed.$client_seed;
echo "Combined seed = $combined_seed\n";
$combined_hash = hash('sha512', $combined_seed);
echo "Hash of combined seed = $combined_hash\n";
$first_four=substr($combined_hash,0,4);
echo "First four characters = $first_four\n";
$hex_to_dec=hexdec($first_four);
echo "Converted to decimal = $hex_to_dec\n";
$weight_array=array(1,17,137,697,2517,6885,14893,26333,39203,50643,58651,63019,64839,65399,65519,65535,65536);
$green_array=array(10,8,6,3,2,1.3,1,0.8,0.5,0.8,1,1.3,2,3,6,8,10);
$red_array=array(20,7,5,3,2,1.1,1,0.6,1,0.6,1,1.1,2,3,5,7,20);
$blue_array=array(50,8,3,2,1.4,1.2,1.1,1,0.4,1,1.1,1.2,1.4,2,3,8,50);
$yellow_array=array(650,30,7,3,1.5,1.2,1,0.7,0.7,0.7,1,1.2,1.5,3,7,30,650);
$i=0;
while ( $hex_to_dec >= $weight_array[$i] ) {
$i++;
}
echo "Green win = \t$green_array[$i]\n";
echo "Red win = \t$red_array[$i]\n";
echo "Blue win = \t$blue_array[$i]\n";
echo "Yellow win = \t$yellow_array[$i]\n";

// Procedure
// 1. Join server and client seeds, server seed first.
// 2. Generate a SHA-512 hash of the string from step 1.
// 3. Convert first FOUR characters of the hash from hexidecimal to decimal.
// 4. Convert result from step 3 to a win per the arrays given.
?>

BGAMING Rules

plinko

BGAMING follows the same concept of balls dropping down a Galton Board. The player may choose from 8 to 16 rows as well as low, medium, or high volatility.

To keep this page from running too long, I present one table for each number of rows, showing the pay tables and return for all three pay tables. The Position column shows how many positions away from the left-most position the ball lands.

Top 8 BGAMING casinos View All

Bitspin365
Players rated Bitspin365 4.3 out of 5 Stars

Sign Up Bonus

500% up to
$10000

New Customer Offer. T&C’s Apply. 18+.This offer is not available for players residing in Ontario. New Customer Offer. T&C’s Apply. 19+. Play Responsibly. Minimum deposit: $20. Allowed games: Rival NP slots only. Max cashout: 10x deposit amount. 
US-OH Friendly
Visit Casino
WinPort Casino
Players rated WinPort Casino 4.1 out of 5 Stars

No Deposit


$30

New customers only. T&C's apply. 18+.This offer is not available for players residing in Ontario. The wagering requirements for Free Chip are 53x, allowing to cash out $60. Applies to all games except titles by Dragon game provider, All Roulette Games, Ride'em Poker, Baccarat, Pai Gow, Craps, Caribbean Poker, Top Card Trumps (Casino War), Draw High Low, Pontoon 21, Pirate 21, Red Dog, Oasis Poker.
US-OH Friendly
Visit Casino
Slots.lv
Players rated Slots.lv 4 out of 5 Stars

Sign Up Bonus

100% up to
$2000

+20 spins

New Customer Offer. T&C’s Apply. 18+. This offer is not available for players residing in Ontario. New customers only. T&C apply. 19+. PLUS 20 Free Spins on Golden Buffalo. Min Deposit 20€. Cashable Bonus.
WOO seal
Wizard Of Odds - Approved
US-OH Friendly
Visit Casino
Bovada Casino
Players rated Bovada Casino 3.9 out of 5 Stars

Sign Up Bonus

100% up to
$1000

New Customer Offer. T&C’s Apply. 18+. Min Deposit: $20. 2nd & 3rd deposits: 100%  up to $1000 - bonus code BV2NDCWB. 
WOO seal
Wizard Of Odds - Approved
US-OH Friendly
Visit Casino
Rich Palms Casino
Players rated Rich Palms Casino 3.8 out of 5 Stars

Sign Up Bonus

300% up to
$3000

New Customer Offer. T&C’s Apply. 18+. This offer is not available for players residing in Ontario. New Customer Offer. T&C’s Apply. 19+. 250% bonus on first deposit plus 50% for crypto deposits. Valid for slots.  Min deposit $25 ( Neosurf $10+). Max cashout: 20x.
WOO seal
Wizard Of Odds - Approved
US-OH Friendly
Visit Casino
Decode Casino
Players rated Decode Casino 3.8 out of 5 Stars

No Deposit Bonuns


$10

New Customer Offer. T&C’s Apply. 18+.This offer is not available for players residing in Ontario. New Customer Offer. T&C’s Apply. 19+. Play Responsibly.  Max cashout: $200.
US-OH Friendly
Visit Casino
Casino Adrenaline
Players rated Casino Adrenaline 3.7 out of 5 Stars

Cashback Bonus

30%

Up to 30% Weekly Cash back based on player class. Newbie 10%, Bronze 10%, Silver 10%, Gold 15%, Platinum 20%, Super Platinum 30%, Diamond 30%. Monday cashback has 5X Max cashout.
US-OH Friendly
Visit Casino
Highway Casino
Players rated Highway Casino 3.7 out of 5 Stars

No Deposit Bonus


$30

New players only. T&Cs apply. 18+. This offer is not available for players residing in Ontario. New Customer Offer. T&C’s Apply. 19+. $30 Free Chip. Players need to sign up from our link, activate bonus code in profile (email should be verified). Maximum cashout: $60. Restricted games: No. Max bet amount for no deposit bonuses: no restrictions.
US-OH Friendly
Visit Casino

16 Rows

Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 16 110 1000 1 0.000015 0.001678 0.001678 0.015259
1 9 41 130 16 0.000244 0.010010 0.010010 0.031738
2 2 10 26 120 0.001831 0.018311 0.018311 0.047607
3 1.4 5 9 560 0.008545 0.042725 0.042725 0.076904
4 1.4 3 4 1,820 0.027771 0.083313 0.083313 0.111084
5 1.2 1.5 2 4,368 0.066650 0.099976 0.099976 0.133301
6 1.1 1 0.2 8,008 0.122192 0.122192 0.122192 0.024438
7 1 0.5 0.2 11,440 0.174561 0.087280 0.087280 0.034912
8 0.5 0.3 0.2 12,870 0.196381 0.058914 0.058914 0.039276
9 1 0.5 0.2 11,440 0.174561 0.087280 0.087280 0.034912
10 1.1 1 0.2 8,008 0.122192 0.122192 0.122192 0.024438
11 1.2 1.5 2 4,368 0.066650 0.099976 0.099976 0.133301
12 1.4 3 4 1,820 0.027771 0.083313 0.083313 0.111084
13 1.4 5 9 560 0.008545 0.042725 0.042725 0.076904
14 2 10 26 120 0.001831 0.018311 0.018311 0.047607
15 9 41 130 16 0.000244 0.010010 0.010010 0.031738
16 16 110 1000 1 0.000015 0.001678 0.001678 0.015259
Total       65,536 1.000000 0.989883 0.989883 0.989764

15 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 15 88 620 1 0.000031 0.002686 0.002686 0.018921
1 8 18 83 15 0.000458 0.008240 0.008240 0.037994
2 3 11 27 105 0.003204 0.035248 0.035248 0.086517
3 2 5 8 455 0.013885 0.069427 0.069427 0.111084
4 1.5 3 3 1,365 0.041656 0.124969 0.124969 0.124969
5 1.1 1.3 0.5 3,003 0.091644 0.119138 0.119138 0.045822
6 1 0.5 0.2 5,005 0.152740 0.076370 0.076370 0.030548
7 0.7 0.3 0.2 6,435 0.196381 0.058914 0.058914 0.039276
8 0.7 0.3 0.2 6,435 0.196381 0.058914 0.058914 0.039276
9 1 0.5 0.2 5,005 0.152740 0.076370 0.076370 0.030548
10 1.1 1.3 0.5 3,003 0.091644 0.119138 0.119138 0.045822
11 1.5 3 3 1,365 0.041656 0.124969 0.124969 0.124969
12 2 5 8 455 0.013885 0.069427 0.069427 0.111084
13 3 11 27 105 0.003204 0.035248 0.035248 0.086517
14 8 18 83 15 0.000458 0.008240 0.008240 0.037994
15 15 88 620 1 0.000031 0.002686 0.002686 0.018921
Total       32,768 1.000000 0.989984 0.989984 0.990265

14 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 7.1 58 420 1 0.000061 0.003540 0.003540 0.025635
1 4 15 56 14 0.000854 0.012817 0.012817 0.047852
2 1.9 7 18 91 0.005554 0.038879 0.038879 0.099976
3 1.4 4 5 364 0.022217 0.088867 0.088867 0.111084
4 1.3 1.9 1.9 1,001 0.061096 0.116083 0.116083 0.116083
5 1.1 1 0.3 2,002 0.122192 0.122192 0.122192 0.036658
6 1 0.5 0.2 3,003 0.183289 0.091644 0.091644 0.036658
7 0.5 0.2 0.2 3,432 0.209473 0.041895 0.041895 0.041895
8 1 0.5 0.2 3,003 0.183289 0.091644 0.091644 0.036658
9 1.1 1 0.3 2,002 0.122192 0.122192 0.122192 0.036658
10 1.3 1.9 1.9 1,001 0.061096 0.116083 0.116083 0.116083
11 1.4 4 5 364 0.022217 0.088867 0.088867 0.111084
12 1.9 7 18 91 0.005554 0.038879 0.038879 0.099976
13 4 15 56 14 0.000854 0.012817 0.012817 0.047852
14 7.1 58 420 1 0.000061 0.003540 0.003540 0.025635
Total       16,384 1.000000 0.989941 0.989941 0.989783

13 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 8.1 43 260 1 0.000122 0.005249 0.005249 0.031738
1 4 13 37 13 0.001587 0.020630 0.020630 0.058716
2 3 6 11 78 0.009521 0.057129 0.057129 0.104736
3 1.9 3 4 286 0.034912 0.104736 0.104736 0.139648
4 1.2 1.3 1 715 0.087280 0.113464 0.113464 0.087280
5 0.9 0.7 0.2 1,287 0.157104 0.109973 0.109973 0.031421
6 0.7 0.4 0.2 1,716 0.209473 0.083789 0.083789 0.041895
7 0.7 0.4 0.2 1,716 0.209473 0.083789 0.083789 0.041895
8 0.9 0.7 0.2 1,287 0.157104 0.109973 0.109973 0.031421
9 1.2 1.3 1 715 0.087280 0.113464 0.113464 0.087280
10 1.9 3 4 286 0.034912 0.104736 0.104736 0.139648
11 3 6 11 78 0.009521 0.057129 0.057129 0.104736
12 4 13 37 13 0.001587 0.020630 0.020630 0.058716
13 8.1 43 260 1 0.000122 0.005249 0.005249 0.031738
Total       8,192 1.000000 0.989941 0.989941 0.990869

12 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 10 33 170 1 0.000244 0.008057 0.008057 0.041504
1 3 11 24 12 0.002930 0.032227 0.032227 0.070313
2 1.6 4 8.1 66 0.016113 0.064453 0.064453 0.130518
3 1.4 2 2 220 0.053711 0.107422 0.107422 0.107422
4 1.1 1.1 0.7 495 0.120850 0.132935 0.132935 0.084595
5 1 0.6 0.2 792 0.193359 0.116016 0.116016 0.038672
6 0.5 0.3 0.2 924 0.225586 0.067676 0.067676 0.045117
7 1 0.6 0.2 792 0.193359 0.116016 0.116016 0.038672
8 1.1 1.1 0.7 495 0.120850 0.132935 0.132935 0.084595
9 1.4 2 2 220 0.053711 0.107422 0.107422 0.107422
10 1.6 4 8.1 66 0.016113 0.064453 0.064453 0.130518
11 3 11 24 12 0.002930 0.032227 0.032227 0.070313
12 10 33 170 1 0.000244 0.008057 0.008057 0.041504
Total       4,096 1.000000 0.989893 0.989893 0.991162

11 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 8.4 24 120 1 0.000488 0.011719 0.011719 0.058594
1 3 6 14 11 0.005371 0.032227 0.032227 0.075195
2 1.9 3 5.2 55 0.026855 0.080566 0.080566 0.139648
3 1.3 1.8 1.4 165 0.080566 0.145020 0.145020 0.112793
4 1 0.7 0.4 330 0.161133 0.112793 0.112793 0.064453
5 0.7 0.5 0.2 462 0.225586 0.112793 0.112793 0.045117
6 0.7 0.5 0.2 462 0.225586 0.112793 0.112793 0.045117
7 1 0.7 0.4 330 0.161133 0.112793 0.112793 0.064453
8 1.3 1.8 1.4 165 0.080566 0.145020 0.145020 0.112793
9 1.9 3 5.2 55 0.026855 0.080566 0.080566 0.139648
10 3 6 14 11 0.005371 0.032227 0.032227 0.075195
11 8.4 24 120 1 0.000488 0.011719 0.011719 0.058594
Total       2,048 1.000000 0.990234 0.990234 0.991602

10 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 8.9 22 76 1 0.000977 0.021484 0.021484 0.074219
1 3 5 10 10 0.009766 0.048828 0.048828 0.097656
2 1.4 2 3 45 0.043945 0.087891 0.087891 0.131836
3 1.1 1.4 0.9 120 0.117188 0.164063 0.164063 0.105469
4 1 0.6 0.3 210 0.205078 0.123047 0.123047 0.061523
5 0.5 0.4 0.2 252 0.246094 0.098438 0.098438 0.049219
6 1 0.6 0.3 210 0.205078 0.123047 0.123047 0.061523
7 1.1 1.4 0.9 120 0.117188 0.164063 0.164063 0.105469
8 1.4 2 3 45 0.043945 0.087891 0.087891 0.131836
9 3 5 10 10 0.009766 0.048828 0.048828 0.097656
10 8.9 22 76 1 0.000977 0.021484 0.021484 0.074219
Total       1,024 1.000000 0.989063 0.989063 0.990625

9 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 5.6 18 43 1 0.001953 0.035156 0.035156 0.083984
1 2 4 7 9 0.017578 0.070313 0.070313 0.123047
2 1.6 1.7 2 36 0.070313 0.119531 0.119531 0.140625
3 1 0.9 0.6 84 0.164063 0.147656 0.147656 0.098438
4 0.7 0.5 0.2 126 0.246094 0.123047 0.123047 0.049219
5 0.7 0.5 0.2 126 0.246094 0.123047 0.123047 0.049219
6 1 0.9 0.6 84 0.164063 0.147656 0.147656 0.098438
7 1.6 1.7 2 36 0.070313 0.119531 0.119531 0.140625
8 2 4 7 9 0.017578 0.070313 0.070313 0.123047
9 5.6 18 43 1 0.001953 0.035156 0.035156 0.083984
Total       512 1.000000 0.991406 0.991406 0.990625

8 Rows

Position Low
Risk Pays		 Medium
Risk Pays		 High
Risk Pays		 Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 5.6 13 29 1 0.003906 0.050781 0.050781 0.113281
1 2.1 3 4 8 0.031250 0.093750 0.093750 0.125000
2 1.1 1.3 1.5 28 0.109375 0.142188 0.142188 0.164063
3 1 0.7 0.3 56 0.218750 0.153125 0.153125 0.065625
4 0.5 0.4 0.2 70 0.273438 0.109375 0.109375 0.054688
5 1 0.7 0.3 56 0.218750 0.153125 0.153125 0.065625
6 1.1 1.3 1.5 28 0.109375 0.142188 0.142188 0.164063
7 2.1 3 4 8 0.031250 0.093750 0.093750 0.125000
8 5.6 13 29 1 0.003906 0.050781 0.050781 0.113281
Total       256 1.000000 0.989063 0.989063 0.990625

The final table shows the return for all number of rows and risk levels.

BGAMING Summary

Rows Low
Risk Return		 Medium
Risk Return		 High
Risk Return
8 98.91% 98.91% 99.06%
9 99.14% 99.14% 99.06%
10 98.91% 98.91% 99.06%
11 99.02% 99.02% 99.16%
12 98.99% 98.99% 99.12%
13 98.99% 98.99% 99.09%
14 98.99% 98.99% 98.98%
15 99.00% 99.00% 99.03%
16 98.99% 98.99% 98.98%

BetFury

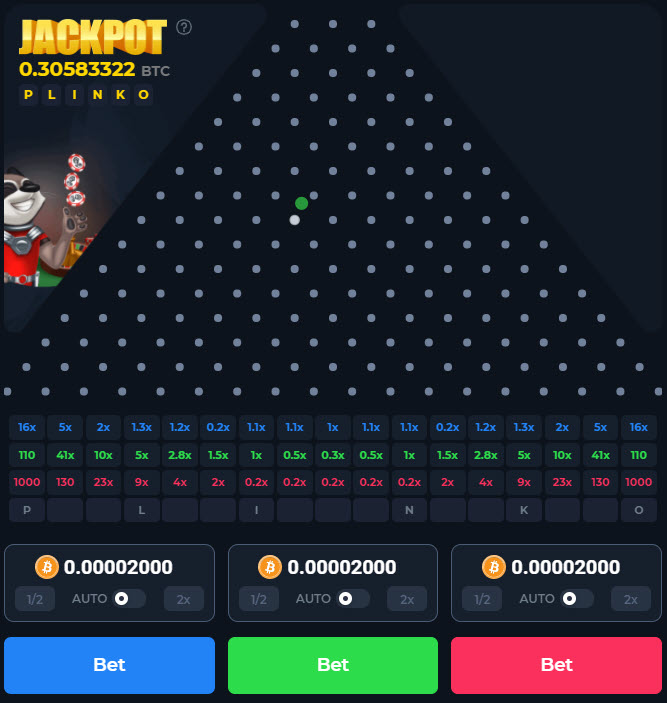
BetFury has their own proprietary Plinko game. It has 16 rows and the pays are similar to the 16-row BGaming game. They are exactly the same between the BGaming "high risk" and the BetFury Red pays.

The following table shows what all three betting options pay, probability of winning, and return to the contribution.

BetFury Casino
Players rated BetFury Casino 3.4 out of 5 Stars

Sign Up Bonus

150%

+50 spins

New Customer Offer. T&C’s Apply. 18+.  This offer is not available for players residing in Ontario. Canadian customers must be 19+ to participate. Play Responsibly. Plus 50 Free Spins. To activate the boost for the first deposit, you need to make a deposit in the first 10 minutes right after registration (the timer can be seen in the lower right corner of the site). Max bet: $10. There are available games for wagering with the bonus balance in the All games tab in the “Bonus Wagering” category. The bonus balance is not available for Sports Betting, Table Games, Special Games, some Slots and Live Games, as well as for the bonus functionality in the chat: Coindrop, Tips, and Rain. For the wagering requirement please contact casino support. 
Visit Casino

BetFury Plinko

Position Blue Pays Green Pays Red Pays Combinations Probability Low
Risk Return		 Medium
Risk Return		 High
Risk Return
0 16 110 1000 1 0.000015 0.001678 0.001678 0.015259
1 5 41 130 16 0.000244 0.010010 0.010010 0.031738
2 2 10 26 120 0.001831 0.018311 0.018311 0.047607
3 1.3 5 9 560 0.008545 0.042725 0.042725 0.076904
4 1.2 2.8 4 1,820 0.027771 0.077759 0.077759 0.111084
5 0.2 1.5 2 4,368 0.066650 0.099976 0.099976 0.133301
6 1.1 1 0.2 8,008 0.122192 0.122192 0.122192 0.024438
7 1.1 0.5 0.2 11,440 0.174561 0.087280 0.087280 0.034912
8 1 0.3 0.2 12,870 0.196381 0.058914 0.058914 0.039276
9 1.1 0.5 0.2 11,440 0.174561 0.087280 0.087280 0.034912
10 1.1 1 0.2 8,008 0.122192 0.122192 0.122192 0.024438
11 0.2 1.5 2 4,368 0.066650 0.099976 0.099976 0.133301
12 1.2 2.8 4 1,820 0.027771 0.077759 0.077759 0.111084
13 1.3 5 9 560 0.008545 0.042725 0.042725 0.076904
14 2 10 26 120 0.001831 0.018311 0.018311 0.047607
15 5 41 130 16 0.000244 0.010010 0.010010 0.031738
16 16 110 1000 1 0.000015 0.001678 0.001678 0.015259
Total       65,536 1.000000 0.978775 0.978775 0.989764

The bottom row shows the following overall return by bet:

  • Blue: 97.88%
  • Green: 97.88%
  • Red: 98.98%

Written by: Michael Shackleford