On this page
Super Times Pay Keno
Introduction
Super Times Pay Keno plays like ordinary four-card spot keno, except adds random multipliers. For the multiplier feature, the player must add 20% to his bet.
Rules
- The player picks 2 to 8 numbers in the range of 1 to 80 on four different cards.
- The player makes a bet that is evenly divisible by 5. 1/5 of the total bet shall be applied to each of four cards, for a total of 4/5 of the total amount bet. The other 1/5 is a fee to pay for the multiplier feature.
- The game shall randomly determine if the player wins a multiplier.
- If the player does win a multiplier, it can be 2x, 3x, 4x or 5x.
- The game shall draw 20 numbers without replacement from balls numbered 1 to 80.
- The base win shall be according to the number of balls that match the numbers chosen by the player. An example pay table is below.
- If the player did not win a multiplier, then his actual win is the base win. If the player did win a multiplier, then his actual win is the product of the multiplier and the base win.
Example
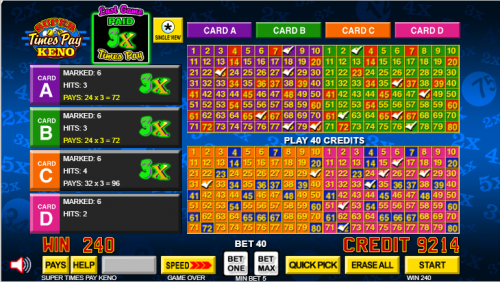
In the image above I picked six numbers on each card. My bet was 10 credits per card, 8 of which went to the base bet and 2 to pay for the multiplier feature.
The game awarded a random multiplier of 3x.
On cards A and B, I caught 3 numbers for a base win of 3. Given by base bet of 8 credits and the multiplier of 3, the total win for that card was 8 × 3 × 3 = 72 for each card.
On card C, I caught 4 numbers for a base win of 4. Given by base bet of 8 credits and the multiplier of 4, the total win for that card was 8 × 4 × 3 = 96.
The total "win" for all four cards was 72+72+96 = 240. Keep in mind I bet 40 credits, so the actual win was 200.
Pay Table 1
The following table shows the weighting of each possible multiplier under pay table 1. A multiplier of 1x is the same as no multiplier at all.
Multiplier Table
| Multiplier | Weight |
|---|---|
| 1 | 63 |
| 2 | 3 |
| 3 | 3 |
| 4 | 2 |
| 5 | 1 |
| Total | 72 |
- Probability of multiplier = 0.12500
- Average multiplier, given multiplier = 3.111111
- Overall average multiplier, including 1x = 1.263889
The next table shows Pay Table 1. The bottom row shows the Return to Player (RTP).
Pay Table 1
| Catch | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 15 | 2 | 2 | 0 | 0 | 0 | 0 |
| 3 | 45 | 5 | 3 | 3 | 1 | 0 | |
| 4 | 85 | 13 | 4 | 2 | 2 | ||
| 5 | 765 | 77 | 28 | 12 | |||
| 6 | 1250 | 437 | 107 | ||||
| 7 | 2500 | 1600 | |||||
| 8 | 2500 | ||||||
| RTP | 93.57% | 93.57% | 93.57% | 93.62% | 93.71% | 93.60% | 93.73% |
Pay Table 2
The following table shows the weighting of each possible multiplier under pay table 2. A multiplier of 1x is the same as no multiplier at all.
Multiplier Table
| Multiplier | Weight |
|---|---|
| 1 | 60 |
| 2 | 3 |
| 3 | 3 |
| 4 | 2 |
| 5 | 1 |
| Total | 69 |
- Probability of multiplier = 0.130435
- Average multiplier, given multiplier = 3.111111
- Overall average multiplier, including 1x = 1.275362
The next table shows Pay Table 2. The bottom row shows the Return to Player (RTP).
Pay Table 2
| Catch | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 14 | 2 | 2 | 0 | 0 | 0 | 0 |
| 3 | 41 | 5 | 3 | 3 | 1 | 0 | |
| 4 | 67 | 12 | 4 | 2 | 2 | ||
| 5 | 700 | 61 | 25 | 12 | |||
| 6 | 1200 | 400 | 90 | ||||
| 7 | 2500 | 1500 | |||||
| 8 | 2500 | ||||||
| RTP | 85.89% | 86.36% | 86.39% | 86.56% | 86.44% | 86.64% | 86.44% |
Pay Table 3
The following table shows the weighting of each possible multiplier under pay table 3. A multiplier of 1x is the same as no multiplier at all.
Multiplier Table
| Multiplier | Weight |
|---|---|
| 1 | 57 |
| 2 | 3 |
| 3 | 3 |
| 4 | 2 |
| 5 | 1 |
| Total | 66 |
- Probability of multiplier = 0.136363
- Average multiplier, given multiplier = 3.111111
- Overall average multiplier, including 1x = 1.287879
The next table shows Pay Table 3. The bottom row shows the Return to Player (RTP).
Pay Table 3
| Catch | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 14 | 2 | 2 | 0 | 0 | 0 | 0 |
| 3 | 41 | 5 | 3 | 3 | 1 | 0 | |
| 4 | 67 | 12 | 4 | 2 | 2 | ||
| 5 | 700 | 62 | 25 | 12 | |||
| 6 | 1200 | 400 | 91 | ||||
| 7 | 2500 | 1500 | |||||
| 8 | 2500 | ||||||
| RTP | 86.73% | 87.20% | 87.24% | 87.41% | 87.61% | 87.49% | 87.53% |
Pay Table 4
The following table shows the weighting of each possible multiplier under pay table 4. A multiplier of 1x is the same as no multiplier at all.
Multiplier Table
| Multiplier | Weight |
|---|---|
| 1 | 55 |
| 2 | 3 |
| 3 | 3 |
| 4 | 2 |
| 5 | 1 |
| Total | 64 |
- Probability of multiplier = 0.140625
- Average multiplier, given multiplier = 3.111111
- Overall average multiplier, including 1x = 1.296875
The next table shows Pay Table 4. The bottom row shows the Return to Player (RTP).
Pay Table 1
| Catch | Pick 2 | Pick 3 | Pick 4 | Pick 5 | Pick 6 | Pick 7 | Pick 8 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 15 | 2 | 2 | 0 | 0 | 0 | 0 |
| 3 | 45 | 5 | 3 | 3 | 1 | 0 | |
| 4 | 85 | 13 | 4 | 2 | 2 | ||
| 5 | 765 | 77 | 28 | 12 | |||
| 6 | 1250 | 437 | 107 | ||||
| 7 | 2500 | 1600 | |||||
| 8 | 2500 | ||||||
| RTP | 93.57% | 93.57% | 93.57% | 93.62% | 93.71% | 93.60% | 93.73% |
External Links
Discussion about Super Times Pay Keno in my forum at Wizard of Vegas.




